Теория Пределов

План
1. Последовательности. Предел последовательности.
2. Функции. Предел функции.
3. Геометрический смысл предела. (самостоятельно
4. Бесконечно малые, бесконечно большие.
5. Основные неопределенности. Замечательные пределы.

Определение: Бесконечной числовой последовательностью (или последовательностью)
называют бесконечное множество чисел (членов последовательности), расположенных в определенном порядке одно за другим и построенных по определенному правилу.

Это правило удобнее задавать в
виде формулы для общего члена последовательности , выражающей функциональную зависимость от целочисленного аргумента , т.е.
Примеры:
Общий член определяет
последовательность

2) Общий член определяет последовательность членов геометрической прогрессии со знаменателем
3) Общий член определяет последовательность

Некоторые последовательности обладают тем свойством, что члены ее по мере роста номера n неограниченно приближаются к постоянному числу а.
Так, например, члены последовательностей 1 и 2 неограниченно приближаются к а = 0, члены последовательности 3 приближаются к а = 1.

Определение: Число в называется пределом функции в точке а, если для всех значений х, достаточно близких к а и отличных от а, значение функции f(х) сколь угодно мало отличается от в.

Функция f(x) называется бесконечно малой при х → а, если
Функция f(x) называется бесконечно большой при х → а, если или

Основные теоремы о пределах
Предел суммы (разности) двух функций равен сумме (разности) их пределов:
Предел произведения двух функций равен произведению их пределов:
Постоянный множитель можно выносить за знак предела:
Функция может иметь только один предел при

Основные теоремы о пределах
Предел степени с натуральным показателем равен той же степени предела:
Предел дроби равен пределу числителя, делённому на предел знаменателя, если предел знаменателя не равен нулю:

Замечательные пределы
I ЗП (первый замечательный предел)
I I ЗП (второй замечательный предел)
или

Непрерывность функции
Функция f (x) называется непрерывной в точке x = a, если предел функции при x→ a равен значению функции при x = a:

Непрерывность функции
Функция f (x) называется непрерывной в точке x = a, если она в этой точке определена и бесконечно малому приращению аргумента соответствует бесконечно малое значение функции:

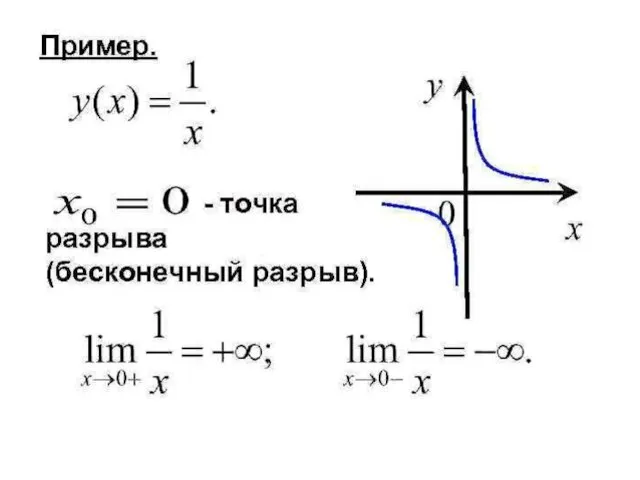
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Для элементарных функций справедливы следующие положения:
область непрерывности элементарной функции совпадает с её областью определения, т.е. элементарная функция непрерывна во всей области определения;
элементарная функция может иметь разрыв только в отдельных точках какого-либо промежутка, но не во всех его точках;
элементарная функция может иметь разрыв только в той точке, в которой она не определена.

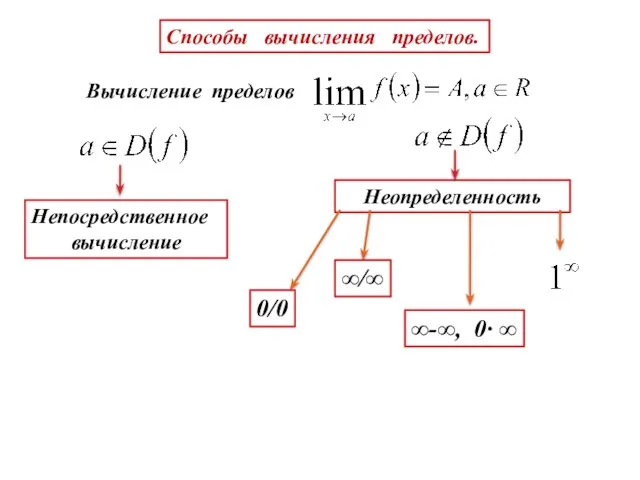
Способы вычисления пределов.
Вычисление пределов
Непосредственное
вычисление
Неопределенность
0/0
∞/∞
∞-∞, 0∙ ∞

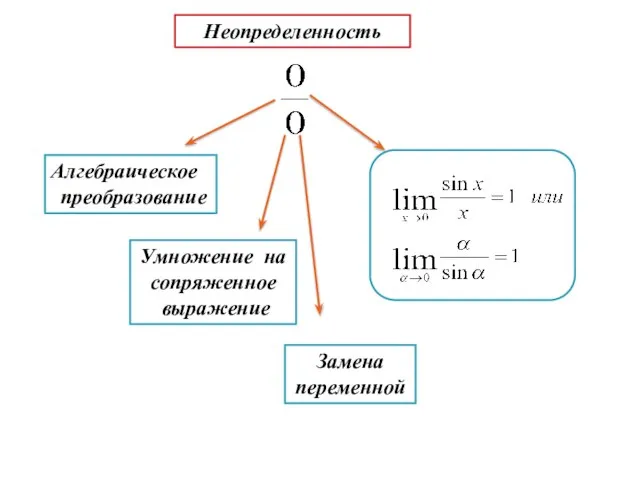
Неопределенность
Алгебраическое
преобразование
Умножение на
сопряженное
выражение
Замена
переменной

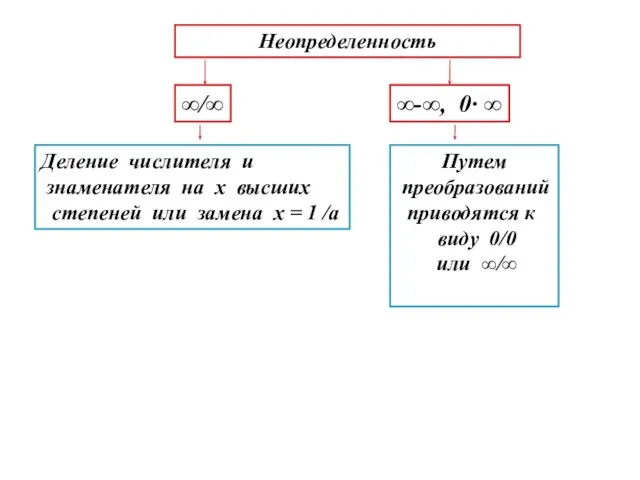
Неопределенность
∞/∞
Деление числителя и
знаменателя на х высших
степеней или замена х = 1 /а
∞-∞, 0∙ ∞
Путем
преобразований
приводятся к
виду 0/0
или ∞/∞

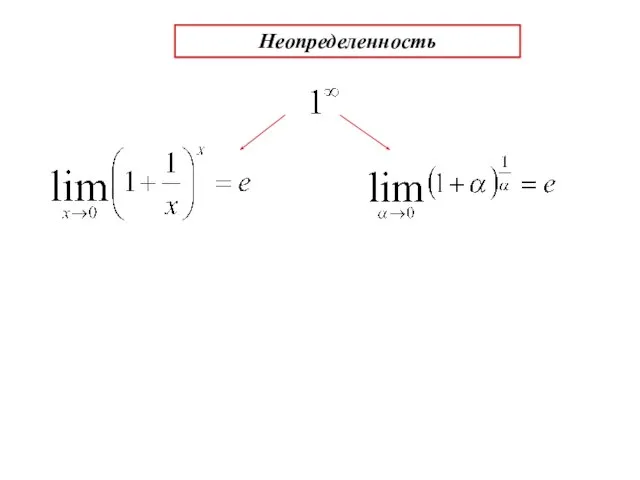
Неопределенность

Запомнить!
С=const (любое постоянное число)

НЕОПРЕДЕЛЕННОСТЬ ∞∕∞
Решение:
Ответ: 2/3.

НЕОПРЕДЕЛЕННОСТЬ ∞∕∞
Решение:
Ответ: - 2,5.

НЕОПРЕДЕЛЕННОСТЬ ∞∕∞
Решение:

НЕОПРЕДЕЛЕННОСТЬ 0 ∕ 0
Решение:

НЕОПРЕДЕЛЕННОСТЬ 0 ∕ 0
Решение:

НЕОПРЕДЕЛЕННОСТЬ 0 ∕ 0
Решение:

НЕОПРЕДЕЛЕННОСТЬ
Решение: