- Главная
- Математика
- Математика в литературе

Содержание
- 2. Часто можно услышать такую фразу: «Ой, да что эта математика! Сухая наука. Выучил формулу- и решай
- 3. Цель работы: доказательство существования связи между литературой и математикой. Задачи: подбор математических задач в литературных произведениях;
- 4. В наши дни литературные журналы не помещают научных, а тем более математических статей на своих страницах,
- 5. В БИБЛИОТЕКЕ А.С. ПУШКИНА ИМЕЛИСЬ ДВА СОЧИНЕНИЯ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ, ОДНО ИЗ КОТОРЫХ ПРЕДСТАВЛЯЕТ СОБОЙ ЗНАМЕНИТЫЙ
- 6. Рассказ Л. Толстого «Много ли человеку земли нужно» « - А цена какая будет? – говорит
- 8. Герои измеряли высоту скалы. Расстояние от колышка до шеста так относится к расстоянию от колышка до
- 9. А. С. Пушкин (1799 – 1837) “Скупой рыцарь” Решение: Даже полчища Атиллы не могли бы воздвигнуть
- 10. Зарецкий тридцать два шага Отмерил с точностью отменной, Друзей развел по крайний след, И каждый взял
- 11. Многие авторы произведений, используя некоторые математические данные, дают возможность читателю подумать над поставленной задачей. Книга позволяет
- 13. Скачать презентацию
Слайд 2Часто можно услышать такую фразу: «Ой, да что эта математика! Сухая наука.
Часто можно услышать такую фразу: «Ой, да что эта математика! Сухая наука.

Слайд 3Цель работы: доказательство существования связи между литературой и математикой.
Задачи:
подбор математических задач
Цель работы: доказательство существования связи между литературой и математикой.
Задачи:
подбор математических задач

решение отобранных задач,
анализ полученных в ходе решения результатов;
оценка проделанной работы и формулировка вывода.
В работе использованы следующие методы:
поиск,
изучение,
анализ,
обобщение,
сравнение.
Актуальность: разрушение стереотипов несовместимости этих наук и доказательство наличия между ними тесного взаимодействия. Достаточно лишь увидеть за словом число, за сюжетом – формулу и убедиться, что литература существует не только для литераторов, а математика – не только для математиков.
Слайд 4 В наши дни литературные журналы не помещают научных,
а тем более
В наши дни литературные журналы не помещают научных, а тем более

А.С.Грибоедов в 1826 г. просил прислать ему учебник по дифференциальному исчислению
Гоголь в 1827 г. не только выписывал “Ручную математическую энциклопедию” Перевозчикова, но даже изучал ее.
Слайд 5 В БИБЛИОТЕКЕ А.С. ПУШКИНА ИМЕЛИСЬ ДВА СОЧИНЕНИЯ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ, ОДНО
В БИБЛИОТЕКЕ А.С. ПУШКИНА ИМЕЛИСЬ ДВА СОЧИНЕНИЯ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ, ОДНО

Слайд 6Рассказ Л. Толстого
«Много ли человеку земли нужно»
« - А цена какая
Рассказ Л. Толстого
«Много ли человеку земли нужно»
« - А цена какая

- Цена у нас одна: 1000 рублей за день.
Не понял Пахом.
- Какая же это мера – день? Сколько в ней десятин будет?
- Мы этого, - говорит, - не умеем считать. А мы за день продаем; сколько обойдешь в день, то и твое, а цена дню 1000 рублей.
Удивился Пахом.
- Да ведь это, - говорит, - в день обойти, земли много будет.
- А мы станем на место, где ты облюбуешь, мы стоять будем, а ты иди, делай круг; а с собой скребку возьми и, где надобно, замечай, на углах ямки рой, дернички клади, потом с ямки на ямку плугом проедем. Какой хочешь круг забирай, только до захода солнца приходи к тому месту, с какого взялся. Что обойдешь, то твое».
Фигура, которая получилась у Пахома, имеет вид:
Решение. Найдем площадь участка. По теореме Пифагора x ≈ 13 верст. Тогда S ≈ ½(2+10)*13 = 78 кв. верст.
Так как 1 верста = 1,0668 км ≈ 1,1 км, 1 кв. верста = 1,138 км², то 78 кв. верст ≈ 89 км² ≈ 8900 Га ≈ 8900 десятин.
Ответ: ≈9000 десятин.
8
15
2
2
х
Слайд 8 Герои измеряли высоту скалы.
Расстояние от колышка до шеста так относится к
Герои измеряли высоту скалы.
Расстояние от колышка до шеста так относится к

«Если мы измерим два первых расстояния, то, зная высоту шеста, сможем вычислить четвертый, неизвестный член пропорции, т. е. высоту стены.
«0ба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее - 500 футам. По окончании измерений инженер составил следующую запись:
15:500 = 10:х, 500×10 = 5000,
5000:15 = 333,3.
Ответ: высота гранитной стены равнялась
333 футам».
Жюль Верн «Таинственный остров»
.
Слайд 9
А. С. Пушкин (1799 – 1837)
“Скупой рыцарь”
Решение:
Даже полчища Атиллы не могли
А. С. Пушкин (1799 – 1837)
“Скупой рыцарь”
Решение:
Даже полчища Атиллы не могли

Это всего на 5км больше того, что можно видеть, стоя на ровном месте.
«…И царь мог с высоты с весельем озирать
И дол, покрытый белыми шатрами,
И море, где бежали корабли…»
Слайд 10 Зарецкий тридцать два шага
Отмерил с точностью отменной,
Друзей развел по
Зарецкий тридцать два шага
Отмерил с точностью отменной,
Друзей развел по

И каждый взял свой пистолет,
ХХХ
«Теперь сходитесь».
Хладнокровно,
Еще не целя во врага
Походкой твердой, тихо, ровно
Четыре перешли шага,
Четыре смертные ступени.
Свой пистолет тогда Евгений,
Не преставая наступать,
Стал первым тихо подымать.
Вот пять шагов еще ступили,
И Ленский, жмуря левый глаз,
Стал также целить – но как раз
Онегин выстрелил... Пробили
Часы урочные: поэт
Роняет молча пистолет...
Поставим вопрос: со скольки шагов стрелялись Онегин и Ленский?
Решение. 32 – (4 + 4) – (5 + 5) = 14. Таким образом делаем вывод: Онегин и Ленский стрелялись с расстояния в 14 шагов. Согласитесь, расстояние настолько маленькое, что промахнуться на этой дуэли практически невозможно.
Слайд 11 Многие авторы произведений, используя некоторые математические данные, дают возможность читателю подумать
Многие авторы произведений, используя некоторые математические данные, дают возможность читателю подумать

Книга позволяет открыть свои тайны только тому человеку, кто умеет читать между строк и сам добывать знания, и отвечать на интересующие его
вопросы…

 Решение неравенств с одной переменной
Решение неравенств с одной переменной Презентация на тему Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы
Презентация на тему Решение задач на готовых чертежах. Окружность. Центральные и вписанные углы  Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2)
Пересечение линии и поверхности. Позиционные задачи. (Лекция 8.2) Теория пределов. Лекция 4
Теория пределов. Лекция 4 Разбиение множеств на классы
Разбиение множеств на классы Дифференциальные уравнения
Дифференциальные уравнения Символика. Взаимное расположение точек и прямой
Символика. Взаимное расположение точек и прямой Тема урока: Умножение чисел на сумму
Тема урока: Умножение чисел на сумму Ну, погоди!
Ну, погоди!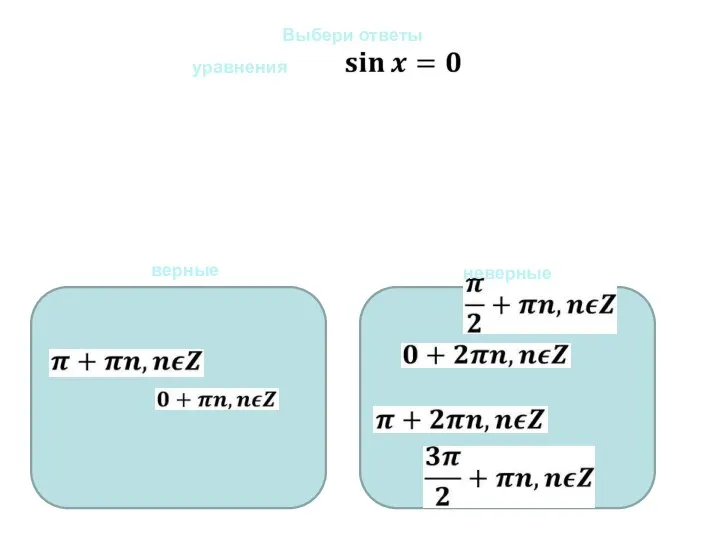 Уравнения sinx=0, cosx=0. Выберите правильный ответ
Уравнения sinx=0, cosx=0. Выберите правильный ответ Задачи, обратные данной
Задачи, обратные данной Презентация на тему Геометрическая прогрессия
Презентация на тему Геометрическая прогрессия  Геометрическая прогрессия
Геометрическая прогрессия Проценты. Примеры цепочкой
Проценты. Примеры цепочкой Презентация на тему Леонтий Филиппович Магницкий
Презентация на тему Леонтий Филиппович Магницкий  Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Разработка обучающей программы по нахождению элементов треугольника
Разработка обучающей программы по нахождению элементов треугольника Степень с рациональным показателем
Степень с рациональным показателем Классификация: общие принципы
Классификация: общие принципы Издательство Легион. Задачи с параметром в ОГЭ
Издательство Легион. Задачи с параметром в ОГЭ Теорема Пифагора. Чертеж к доказательству Пифагора
Теорема Пифагора. Чертеж к доказательству Пифагора Тождественные преобразования рациональных выражений
Тождественные преобразования рациональных выражений Сложение и вычитание в пределах первого десятка
Сложение и вычитание в пределах первого десятка Понятие математической индукции и ее применение
Понятие математической индукции и ее применение Упрощение выражений. Тест
Упрощение выражений. Тест Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Презентация на тему Нахождение дроби от числа. Нахождение числа
Презентация на тему Нахождение дроби от числа. Нахождение числа  Признаки классификации статистической сводки
Признаки классификации статистической сводки