Содержание
- 2. «Дорогу осилит идущий, математику - мыслящий »
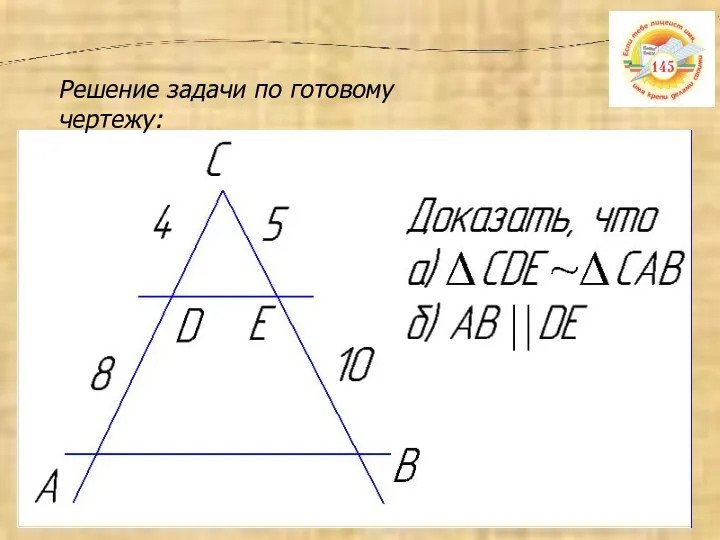
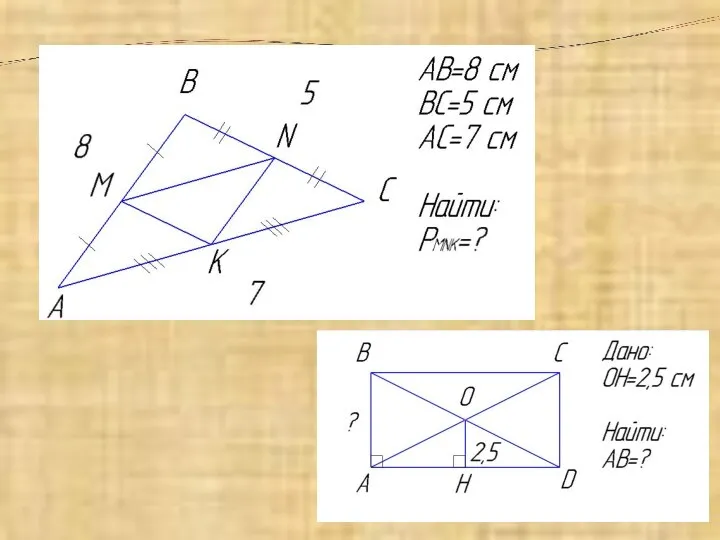
- 3. Решение задачи по готовому чертежу:
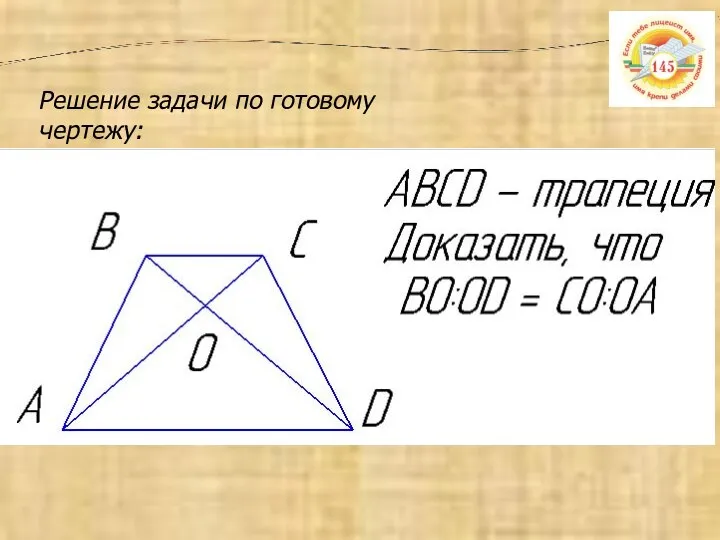
- 4. Решение задачи по готовому чертежу:
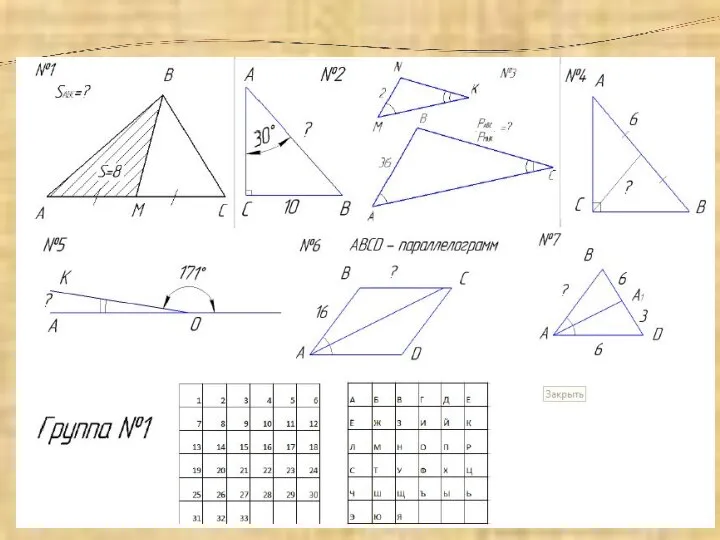
- 5. Задания для групп: 1. Расшифровка слова путем решения геометрических задач 2. Теоретический кроссворд 3. «Теорема-пазл» по
- 7. Кроссворд по терминам 5. Два треугольника с соответственно равными углами и пропорциональными сторонами? 6. Какой древнегреческий
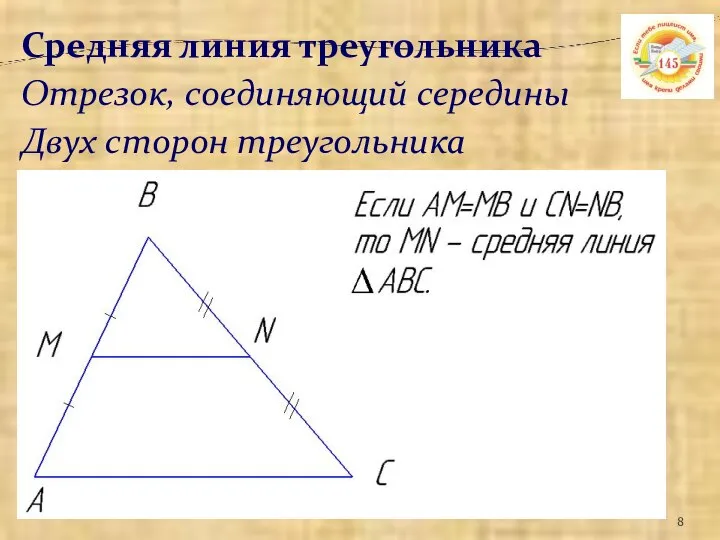
- 8. Средняя линия треугольника Отрезок, соединяющий середины Двух сторон треугольника
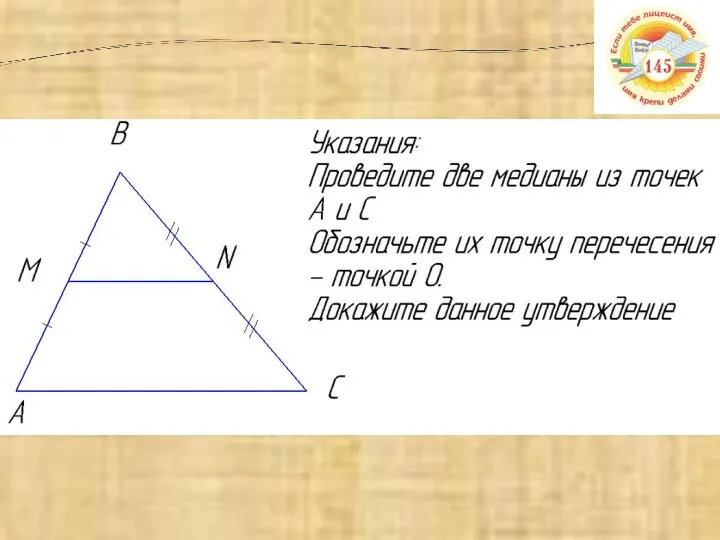
- 9. Исследуйте, какими свойствами обладает средняя линия треугольника? Творческое задание :
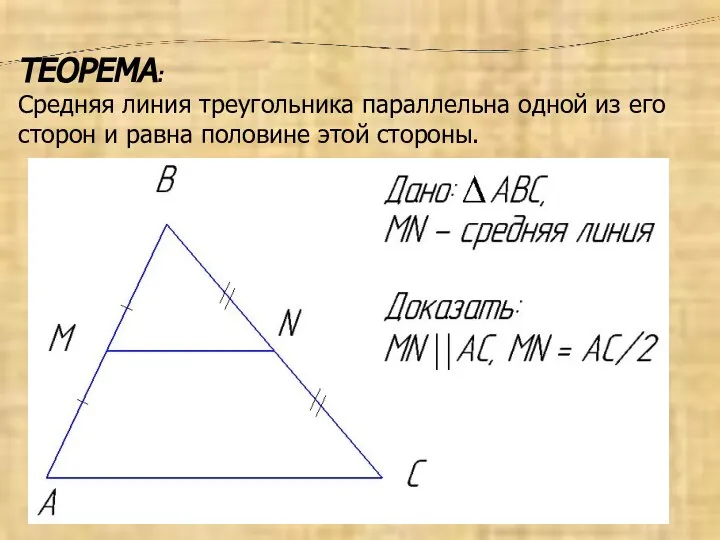
- 10. ТЕОРЕМА: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
- 11. Работа по учебнику: № 564, 565 по готовым чертежам
- 13. Если ответ ДА — поднимаем руку, ответ НЕТ — отрицаем головой. 1. у луча есть концы
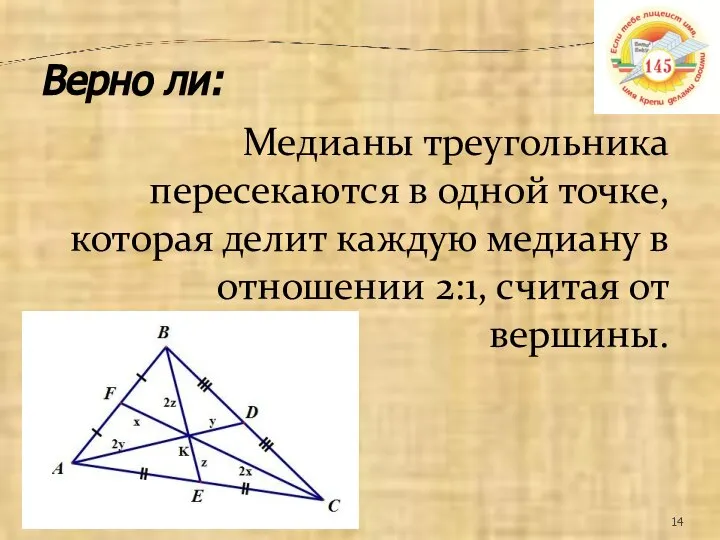
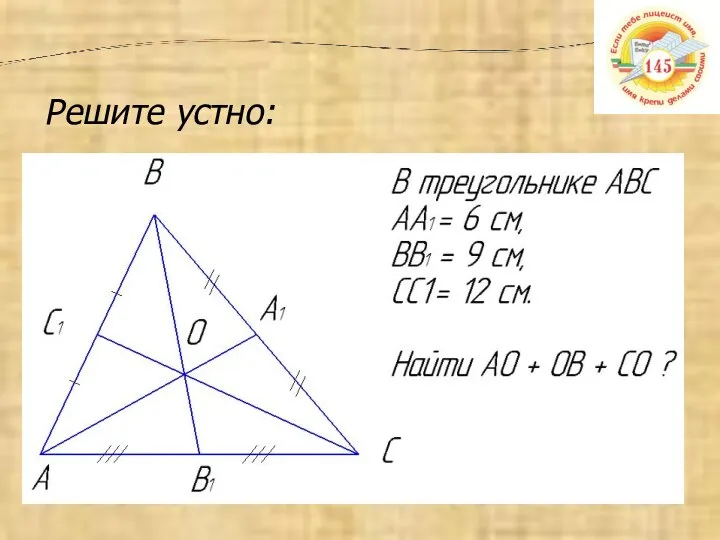
- 14. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
- 16. Решите устно:
- 17. Рефлексия учебной деятельности: 1. Кратко опишите самое важное, что уяснили сегодня на уроке 2. Пожелание себе
- 18. Домашнее задание: п.64 №566, 568 (б), 569 Ответить на вопрос: Как связаны понятия: центр тяжести и
- 20. Скачать презентацию







 Геометрическая прогрессия. Формула n-го члена геометрической прогрессии
Геометрическая прогрессия. Формула n-го члена геометрической прогрессии Интегральное исчисление. Первообразная функция. Неопределённый интеграл
Интегральное исчисление. Первообразная функция. Неопределённый интеграл Сложение и вычитание многозначных чисел
Сложение и вычитание многозначных чисел Координатная плоскость
Координатная плоскость СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ Логарифмы. Определение
Логарифмы. Определение Экономические задачи VI. Задания 1-4, ЕГЭ
Экономические задачи VI. Задания 1-4, ЕГЭ Создание и применение мультимедийных презентаций на уроках математики
Создание и применение мультимедийных презентаций на уроках математики Квадратичная функция и ее свойства
Квадратичная функция и ее свойства Экстремум функции двух переменных. Лекция №6 (УСР)
Экстремум функции двух переменных. Лекция №6 (УСР) Сравнение дробей. 1 часть
Сравнение дробей. 1 часть Параллелограмм и трапеция. Урок 6
Параллелограмм и трапеция. Урок 6 Дифференциальные уравнения
Дифференциальные уравнения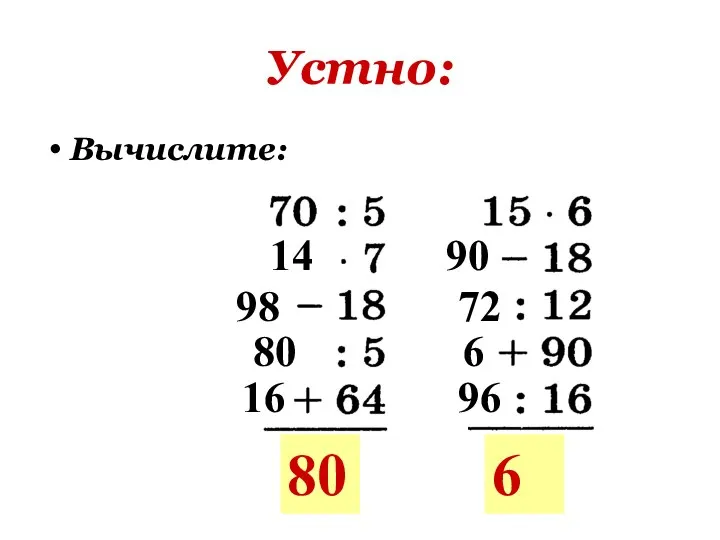 Устно. Вычисления
Устно. Вычисления Презентация на тему Справочное пособие по геометрии
Презентация на тему Справочное пособие по геометрии  Диаграммы
Диаграммы Признаки параллелограмма
Признаки параллелограмма Тема работы: «Систематизация задач с процентами и способы их решения при подготовке к ЕГЭ»
Тема работы: «Систематизация задач с процентами и способы их решения при подготовке к ЕГЭ» Окружность и круг
Окружность и круг Понятие корня
Понятие корня Правила комбинаторики. Основные понятия
Правила комбинаторики. Основные понятия Интегрированный урок алгебры в 8 классе
Интегрированный урок алгебры в 8 классе Множества иррациональных и действительных чисел
Множества иррациональных и действительных чисел Презентация на тему Знаки больше, меньше, равно (1 класс)
Презентация на тему Знаки больше, меньше, равно (1 класс)  Множество. Число элементов множества. Подмножество
Множество. Число элементов множества. Подмножество Фракталы
Фракталы Обратные матрицы
Обратные матрицы