Содержание
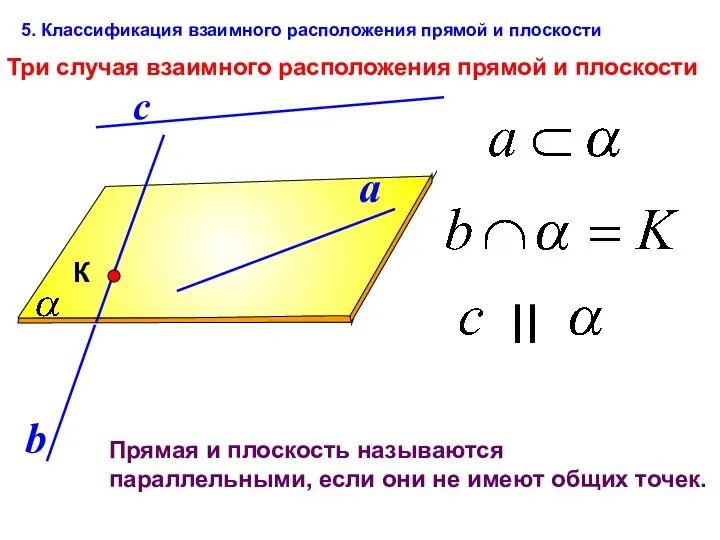
- 2. Три случая взаимного расположения прямой и плоскости Прямая и плоскость называются параллельными, если они не имеют
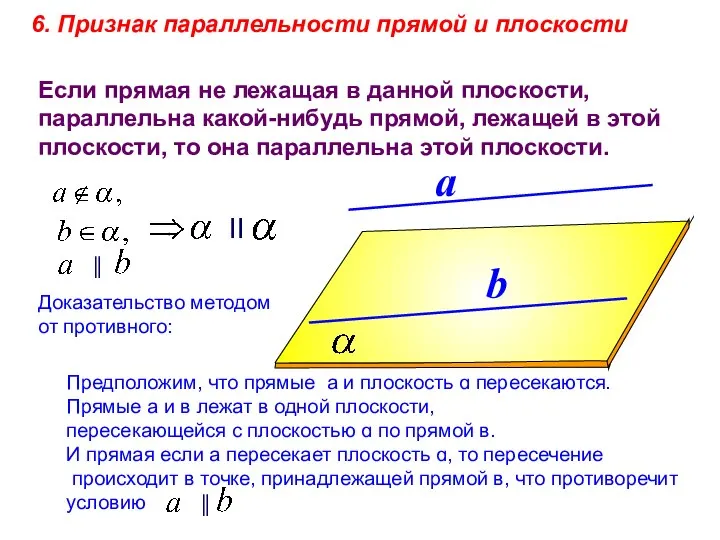
- 3. a b 6. Признак параллельности прямой и плоскости Если прямая не лежащая в данной плоскости, параллельна
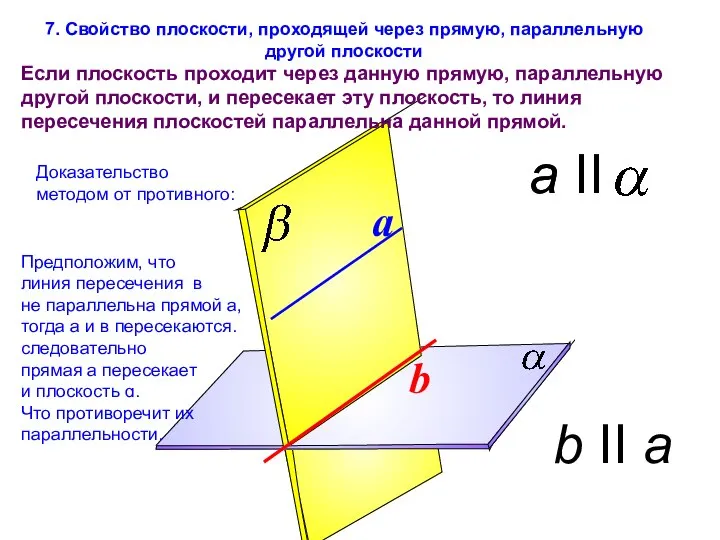
- 4. 7. Свойство плоскости, проходящей через прямую, параллельную другой плоскости Если плоскость проходит через данную прямую, параллельную
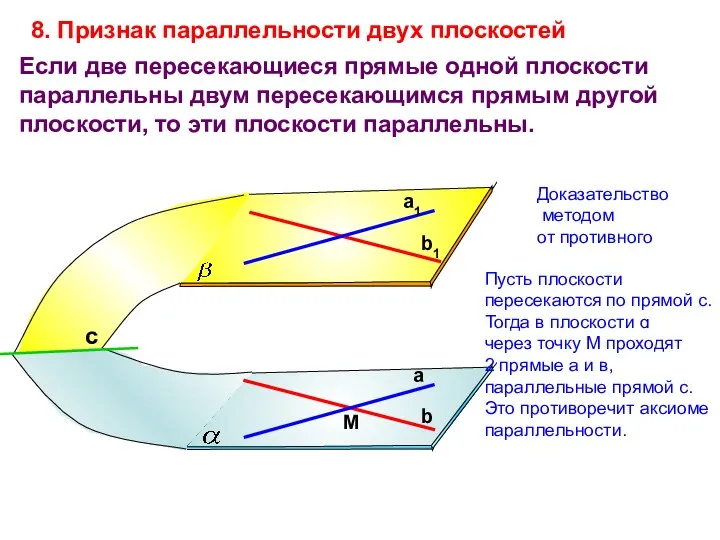
- 5. Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
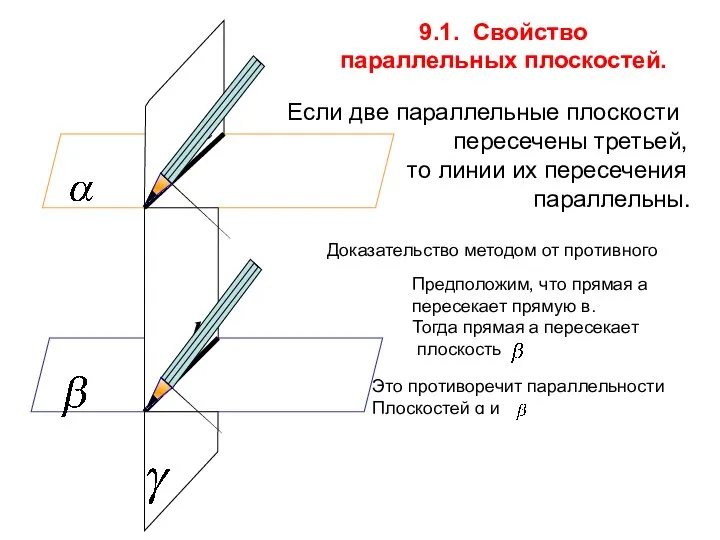
- 6. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. 9.1. Свойство параллельных плоскостей. Доказательство
- 8. Скачать презентацию
 Формальные логические теории
Формальные логические теории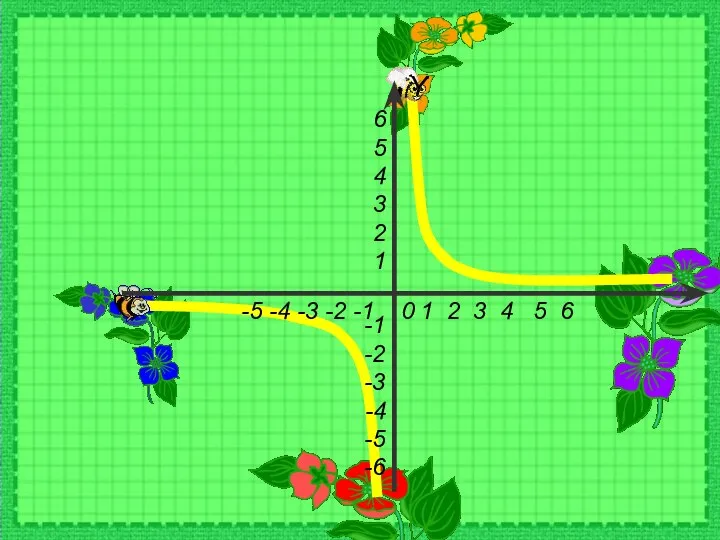 Функция у=1/х и её график
Функция у=1/х и её график Графы. Теория графов
Графы. Теория графов Симметрия в нашей жизни
Симметрия в нашей жизни Помоги ёжику. Интерактивный тренажёр по математике, 1 класс
Помоги ёжику. Интерактивный тренажёр по математике, 1 класс Презентация на тему РЕШЕНИЕ ЗАДАЧ НА НАХОЖДЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ И ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ
Презентация на тему РЕШЕНИЕ ЗАДАЧ НА НАХОЖДЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ И ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ  Единицы измерения объёма
Единицы измерения объёма Prezentatsia_k_uroku_matematiki_v_6_kl
Prezentatsia_k_uroku_matematiki_v_6_kl Действия с десятичными дробями. Математические гонки
Действия с десятичными дробями. Математические гонки Циклический алгоритм
Циклический алгоритм Свойства логарифмов
Свойства логарифмов Квадратные уравнения
Квадратные уравнения Центральные и вписанные углы
Центральные и вписанные углы Число или цифра 5
Число или цифра 5 Длина окружности,
Длина окружности, Презентация на тему Слагаемое сумма
Презентация на тему Слагаемое сумма  Решение задач с помощью дифференциальных уравнений
Решение задач с помощью дифференциальных уравнений Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Признаки параллельности двух прямых
Признаки параллельности двух прямых Линейная алгебра. Метод Гаусса для решения систем линейных алгебраических уравнений
Линейная алгебра. Метод Гаусса для решения систем линейных алгебраических уравнений Изучение таблицы деления
Изучение таблицы деления Усеченый конус
Усеченый конус Логические задачи. Задачи со спичками
Логические задачи. Задачи со спичками Умножение - 3
Умножение - 3 Отображения (функции)
Отображения (функции) Алгебра в жизни человека
Алгебра в жизни человека Задачи на увеличение (уменьшение) числа на несколько единиц
Задачи на увеличение (уменьшение) числа на несколько единиц Сумма углов в треугольнике
Сумма углов в треугольнике