Слайд 2Параметрическая стандартизация
Разработка параметрических стандартов, в которых устанавливаются ряды параметров, характеризующих мощность, производительность,

грузоподъемность и т.д. различных изделий.
Слайд 3Параметрическая стандартизация
Стандартизация, обеспечивающая регламентирование значений параметров, называется параметрической стандартизацией.

Слайд 4Параметрическая стандартизация
При выборе параметров используют параметрические ряды, которые создаются на основе рядов

предпочтительных чисел
Слайд 5Ряды предпочтительных чисел
Должны отвечать требованиям:
Представлять рациональную систему чисел, отвечающую потребностям производства и

эксплуатации;
Быть бесконечным как в сторону малых, так и больших величин;
Включать все десятикратные значения от любого члена ряда;
Быть простыми и легко запоминаемым
Слайд 6Ряды предпочтительных чисел
Ряды предпочтительных чисел бывают двух видов:
ряды ИСО для общепромышленного применения

(приняты в 1953 году Международной организацией по стандартизации);
ряды МЭК для изделий электро- и радиопромышленности.
Слайд 7Ряды предпочтительных чисел
Ряды предпочтительных чисел строятся на основе геометрической
а n= а

1 q n-1
где а n - n-й член ряда
а 1 - первый член ряда
q – знаменатель геометрической прогрессии
Слайд 8Ряды предпочтительных чисел
и арифметической прогрессии:
а n= а 1 + d (n-1),
где а

1 – первый член прогрессии
d – разность прогрессии
n – номер взятого члена
Слайд 9Геометрическая прогрессия
Геометрической прогрессией называется последовательность чисел, в которой величина, равная отношению между

последующим и предыдущим членами остается постоянной.
Она называется знаменателем прогрессии (q)
Слайд 10ГОСТ 8032-84 Предпочтительные числа и ряды предпочтительных чисел
Устанавливает ряды предпочтительных чисел со

знаменателями:
для ряда R5: q = 5√10 ≈1,6;
для ряда R10: q = 10√10 ≈1,25;
для ряда R20: q = 20√10 ≈1,12;
для ряда R40: q = 40√10 ≈1,06, принятых в качестве основных.
Они называются основными рядами.
Слайд 11ГОСТ 8032-84 Предпочтительные числа и ряды предпочтительных чисел
1-й ряд R5 - 1,00;

1,60; 2,50; 4,00; 6,30; 10,00 …имеет знаменатель прогрессии 5√10 ≈1,6;
2-й ряд R10 - 1,00; 1,25;1,60; 2,00; 2,50; … имеет знаменатель прогрессии 10√ 10 ≈1,25;
3-й ряд R20 - 1,00; 1,12; 1.25;1,40; 1,60 … имеет знаменатель прогрессии 20√ 10 ≈1,12;
…………………………………………………………
Количество чисел в интервале 1-10:
для ряда R5 – 5;
для ряда R10 – 10;
для ряда R20 - 20;…………………………
Слайд 12ГОСТ 8032-84 Предпочтительные числа и ряды предпочтительных чисел
В технически обоснованных случаях стандартом

допускается применение дополнительных рядов:
R80 со знаменателем q = 80√ 10 ≈1,0 и
R160 со знаменателем q = 160√ 10 ≈1,015
Слайд 13Ряды предпочтительных чисел
Обозначения рядов, не ограниченных пределами: R5; R10; R20; R40; R80;

R160.
Обозначения рядов, ограниченных пределами и числами:
R5 (…40…) – основной ряд R5, не ограниченный верхним и нижним пределом, но с обязательным включением члена 40;
R10 (1,25…) - основной ряд R10, ограниченный членом 1,25 в качестве нижнего предела;
R40 (75…300) основной ряд R40, ограниченный членом 75 в качестве нижнего предела и членом 300 в качестве верхнего предела.
Слайд 14Выборочные ряды предпочтительных чисел
Образуются на базе основных рядов и обозначаются:
R5/2 (1...1000000) –ряд,

полученный путем отбора каждого второго члена основного ряда R5 и ограниченный членами 1…10000000;
R10/3 (…80…) - ряд, полученный путем отбора каждого третьего члена основного ряда R10, включающий число 80 и неограниченный в обоих направлениях
Например, выборочный ряд R10/3 (1…) будет состоять из членов: 1; 2; 4; 8; 16; 31,5…;
выборочный ряд R20/2 (1,12…) из членов 1,12; 1,4; 1,8; 2,24; 2,80 …
Слайд 15Использование параметрических рядов, основанных на основе геометрической прогрессии
Для создание параметрических стандартов рядов

параметров
изделий, характеризующих мощность, производительность,
грузоподъемность и т.д. с целью согласования параметров
изделий между собой.
Например, объем ковша экскаватора должен быть согласован
с объемом кузова автомобиля, а технологические
характеристики металлургического и прокатного
оборудования д.б.увязаны не только между собой, но и с
характеристиками прессов, металлорежущих станков и
др.технологического оборудования.
Слайд 16Арифметическая прогрессия
Арифметической прогрессией называется последовательность чисел, в которой разность между последующим и

предыдущим членами остается неизменной.
Эта неизменная разность называется разностью прогрессии (d).
Слайд 17Арифметические предпочтительные ряды
В обозначениях указывают их разность и числа, ограничивающие ряд:
А5;
А2

(-10, …,+10) и т.д.,
где А-обозначение арифметического предпочтительного ряда;
2 и 5 – значения разности;
-10 и +10 –числа ограничивающие ряд.
Например, при а1=1 и знаменателе прогрессии d=2, получим ряд: 1; 3; 5; 7; 9; и т.д.
Слайд 18Использование рядов предпочтительных чисел, основанных на арифметической прогрессии
Арифметические предпочтительные ряды применяют при

установлении таких параметров продукции как:
температура окружающего воздуха;
размеры обуви, одежды;
уровень шума и т.д.
Слайд 19Использование рядов предпочтительных чисел, основанных на арифметической прогрессии
Ряды с арифметической прогрессией используются

очень редко, когда диапазон значений параметра невелик.
Например, в диапазоне от 3,15 до 50 мм для ряда диаметров труб, состоящего из 7 диаметров, на основе арифметической прогрессии со знаменателем 7,81 получим диаметры: 3,15; 10,96, 18,77; 26,58 , 34,39; 42,20; 50 мм.
Слайд 20Использование рядов предпочтительных чисел
Ряды предпочтительных чисел на основе геометрической прогрессии являются предпочтительными,

т. к. они наибольшим образом удовлетворяют следующим требованиям:
представляют рациональную систему градаций, отвечающую потребностям производства и эксплуатации;
просты и легко запоминаются;
включают все последовательные десятикратные или дробные значения каждого числа.
Слайд 21Приближенные ряды предпочтительных чисел
В технически обоснованных случаях (например, число зубьев шестерен не

может быть дробным числом 31,5), требуются дополнительные округления стандартизованных предпочтительных чисел основного ряда.
В ГОСТ 8032-84 приближенные ряды обозначаются R’ или R” в зависимости от величины проведенных округлений.
Слайд 22Свойства основных рядов предпочтительных чисел
1) Если величины, входящие в ряды предпочтительных

чисел, связаны степенной зависимостью, то знаменатели рядов, которые они образуют, также связаны такой же степенной зависимостью.
Слайд 23Свойства основных рядов предпочтительных чисел
диаметры днищ (D) резервуаров в метрах: 1,6; 2,5;

4,0 – ряд R5, со знаменателем
qd = 5√10 ≈1,6;
площадь днища (S), м2 : 2,0; 5,0; и 12,5 отражает ряд R10/4 при
qS = 10√10 ≈ 2,5.
Поскольку 2,5 ≈ 1,62 (неточность объясняется округлением), то можно утверждать, что, если S = К•D2 , где К= π/4, следовательно:
qS = qd 2
Слайд 24Свойства основных рядов предпочтительных чисел
2) Ряды предпочтительных чисел безграничны в обоих направлениях.
2.1)

Для перехода от предпочтительных чисел в любой другой десятичный интервал, нужно умножить эти числа на 10 k, где k целое положительное или отрицательное число - номер интервала по отношению к интервалу от 1 до 10, для которого k = 0. Все десятичные интервалы в сторону увеличения значений будут иметь k≥0, а в сторону уменьшения k- отрицательные.
Слайд 25Свойства основных рядов предпочтительных чисел
2.2) Изменение предпочтительных чисел на 10k сводится к

переносу запятой, входящей в каждое число, на k знаков вправо (при +k) или влево (при –k).
Например:
5,00·103 = 5000 - вправо на 3-и знака
1,18 ·10-2 = 0,0118-влево на 2-а знака
Слайд 26Свойства основных рядов предпочтительных чисел
2.3) Порядковый номер предпочтительного числа N, соответствующий любому

интервалу вычисляется: N=NT+ k·40,
где NT – номер числа в сквозном ряду чисел (k=0).
Например, найти номера чисел: 1000 и 0,0955.
Решение: N1000= N1,00 + 3·40 =120, т.к. N1,00 =0, а число 1000 относится к третьему интервалу ( k=3).
N0,095= N9,50 -- 2·40 = - 41, т.к. N9,50 = 39, а число
0,095 относится к интервалу ( k= - 2).
Слайд 27Свойства основных рядов предпочтительных чисел
3) Связь между номерами (N) предпочтительных чисел и

их значениями выражается в виде:
q0 = 1; q1 = 1,06; q2 = 1,12; q3 = 1.18; … ; q40 = 10,
где 0,1,2,3…40 – порядковые номера чисел в таблице;
1; 1,06; 1,12; 1,18; … 10 – значения чисел в ряду
Слайд 28Свойства основных рядов предпочтительных чисел
Для ускорения вычислений при построении параметрических рядов произведение

или частное членов ряда получают, суммируя или вычитая порядковые номера членов:
N 3,15+ N 1,6=20+8=28
N 1- N 0,06=0 - (49)=49
Номеру 28 соответствует число 5,
номеру 49 – число 17
Слайд 29Параметрическая стандартизация
Основными направлениями работ по параметрической стандартизации является:
стандартизация линейных размеров;
стандартизация параметров

электрических резисторов и емкостей;
стандартизация напряжений и силы тока;
стандартизацию частоты.




























 Credit and exam
Credit and exam Создание геометрических тел
Создание геометрических тел Переход от передаточных функций к дифференциальным уравнениям и структурным схемам
Переход от передаточных функций к дифференциальным уравнениям и структурным схемам Поверхности второго порядка
Поверхности второго порядка Решение задач по теории вероятности. Подготовка к ГИА
Решение задач по теории вероятности. Подготовка к ГИА Старинные русские меры длины
Старинные русские меры длины Сочетания. В чем отличие от размещений?
Сочетания. В чем отличие от размещений? Устный счет
Устный счет Основы теории графов
Основы теории графов Урок математики в 1 классе
Урок математики в 1 классе Сравнение десятичных дробей
Сравнение десятичных дробей Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ
Презентация на тему РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ  Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики
Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики Система MatLab/ Методические указания к выполнению лабораторных работ
Система MatLab/ Методические указания к выполнению лабораторных работ Рисование узора из геометрических фигур
Рисование узора из геометрических фигур Треугольники в окружающем мире
Треугольники в окружающем мире Метод группировки
Метод группировки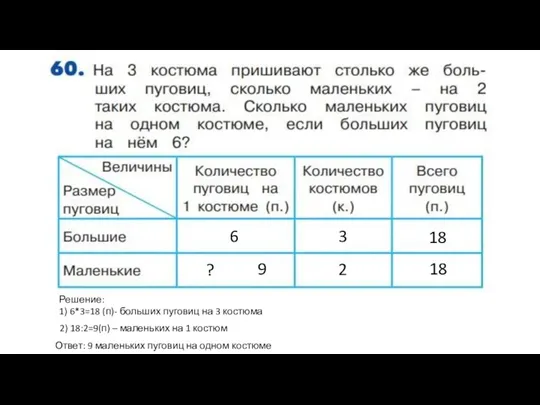 Задача о костюмах
Задача о костюмах Основы теории оболочек вращения
Основы теории оболочек вращения Знакомство с цифрой 5
Знакомство с цифрой 5 Линии и углы в окружности
Линии и углы в окружности Формирование знаковой культуры на уроках
Формирование знаковой культуры на уроках Статистическое наблюдение
Статистическое наблюдение Формула Остроградского - Гаусса
Формула Остроградского - Гаусса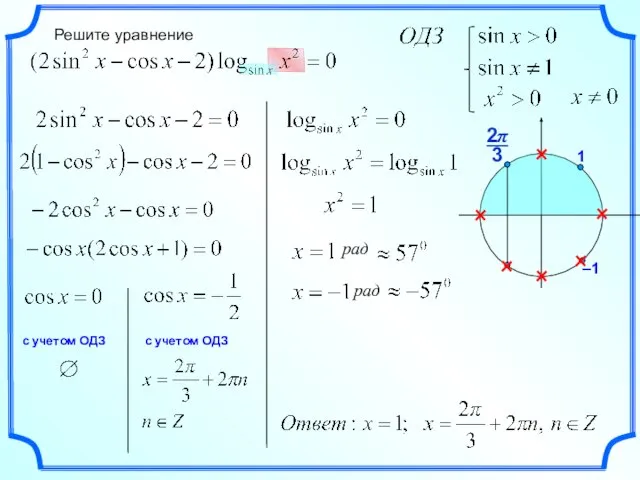 Решение уравнения
Решение уравнения Приемы устного счета
Приемы устного счета Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Состав числа 10
Состав числа 10