Вписанная окружность

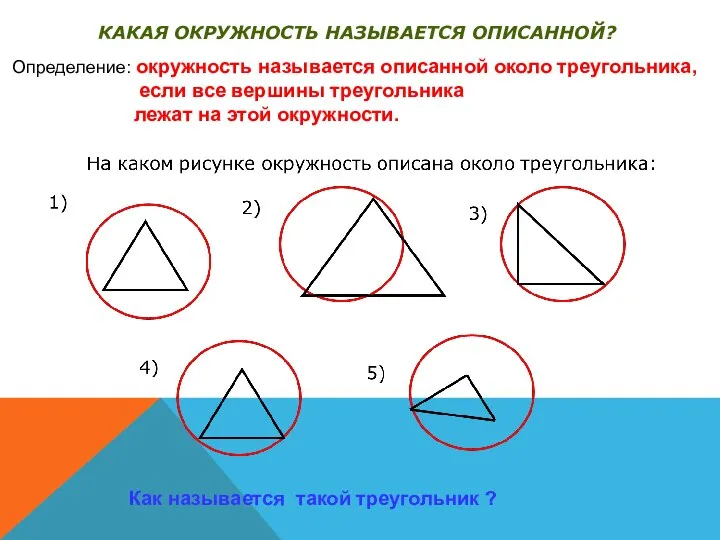
Определение: окружность называется описанной около треугольника,
если все вершины треугольника
лежат на этой окружности.
Как называется такой треугольник ?
КАКАЯ ОКРУЖНОСТЬ НАЗЫВАЕТСЯ ОПИСАННОЙ?

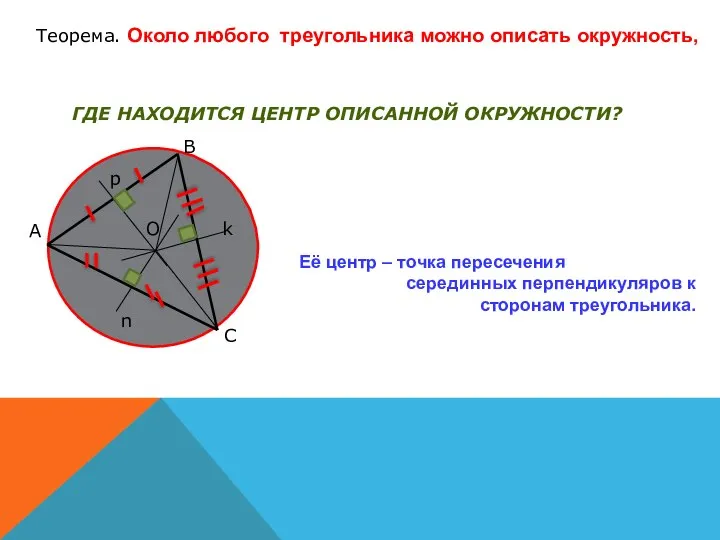
Теорема. Около любого треугольника можно описать окружность,
Её центр – точка пересечения серединных перпендикуляров к сторонам треугольника.
ГДЕ НАХОДИТСЯ ЦЕНТР ОПИСАННОЙ ОКРУЖНОСТИ?

ПРОВЕРИМ ДОМ. РАБОТУ
ВЫПОЛНИМ УСТНО: Р.Т.
№300
№302
№309
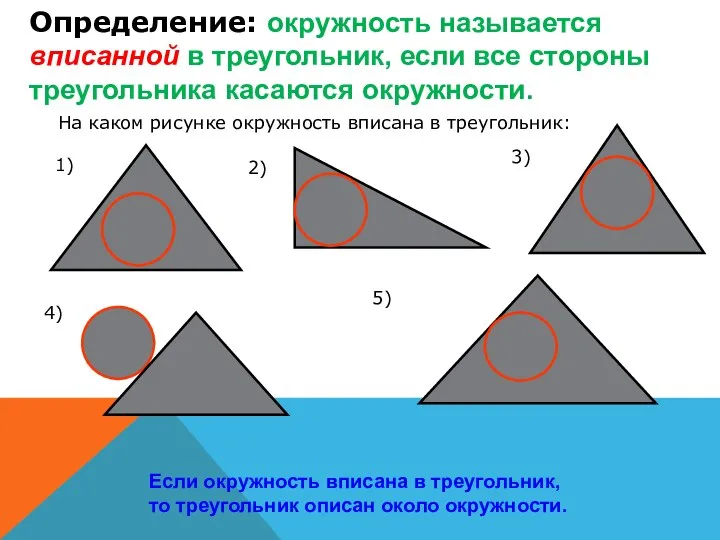
№545

Определение: окружность называется вписанной в треугольник, если все стороны треугольника касаются окружности.
Если окружность вписана в треугольник,
то треугольник описан около окружности.

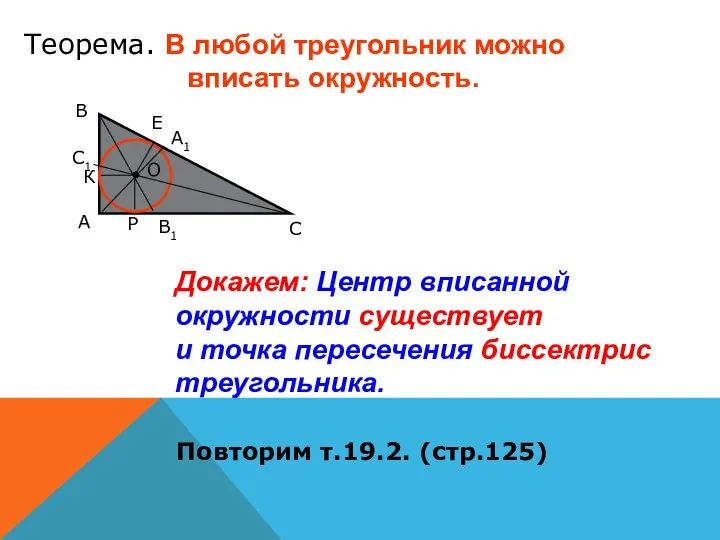
Теорема. В любой треугольник можно
вписать окружность.
Докажем: Центр вписанной окружности существует
и точка пересечения биссектрис треугольника.
Повторим т.19.2. (стр.125)

ВЫПОЛНИМ:
№552