Изоморфные графы

Что такое изоморфизм?
Изоморфизм устанавливает отношение равенства между графами G и Н (G=H – графы изоморфны).
Два графа изоморфны, если между множествами их вершин можно установить взаимно-однозначное соответствие, сохраняющее смежность.
Маленькая проверка: мысленно «деформируйте» один из графов так, чтобы он стал похож на второй. Если получилось, то эти графы изоморфны.
Другими словами, два графа равны, если их соответствующие вершины соединены одинаково.

Например, поиграем в спички: соберём звезду и пятиугольник.
Итак, перед нами две фигуры. Но точно ли они различаются?
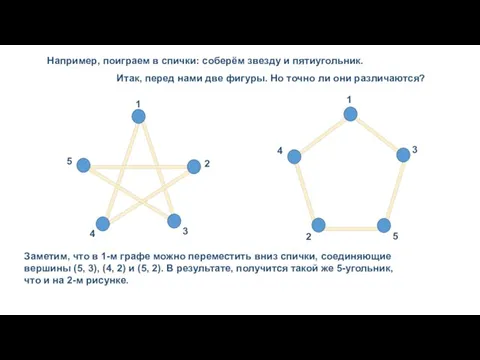
Заметим, что в 1-м графе можно переместить вниз спички, соединяющие вершины (5, 3), (4, 2) и (5, 2). В результате, получится такой же 5-угольник, что и на 2-м рисунке.

СТРОГОЕ ОПРЕДЕЛЕНИЕ
ИЗОМОРФНЫХ ГРАФОВ
Определение
Два графа G=
и H=
(V, W – множества вершин; X, Y – множества ребер) называются изоморфными, если существует биективное отображение ϕ: V→W, сохраняющее смежность, такое, что для вершин u, v∈V (ϕ(u), ϕ(v))∈Y ⇔ (u, v)∈X. В этом случае отображение ϕ называют изоморфизмом.
Пример
Данные графы изоморфны, т.к. между множествами их вершин существует изоморфизм - каждой вершине одного графа соответствует вершина второго графа того же цвета.