Слайд 2Сведения из истории
Современные обозначения arcsin и
arctg появляются в 1772г.в работах
венского

математика Щерфера и
известного французского ученого
Ж.Л. Лагранжа, хотя
несколько ранее уже
рассматривал Д. Бернулли,
который употреблял иную
символику.
Слайд 3Сведения из истории
Общепринятыми эти символы
стали лишь в конце XVIII
столетия. Приставка
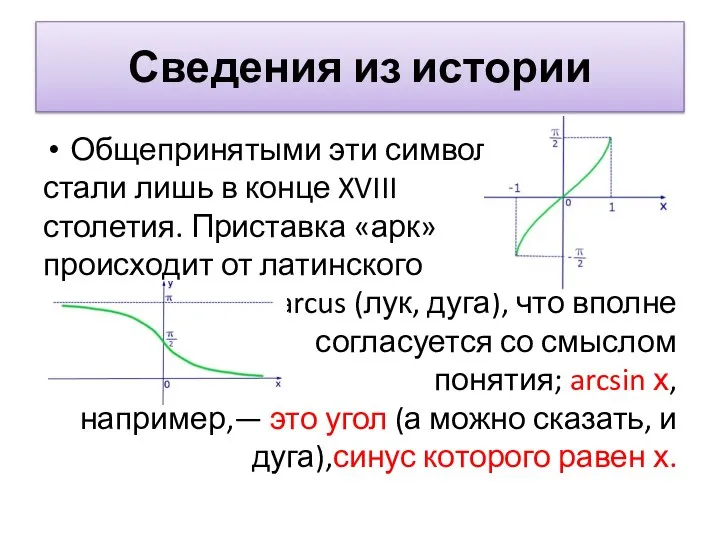
«арк»
происходит от латинского
arcus (лук, дуга), что вполне
согласуется со смыслом
понятия; arcsin х,
например,— это угол (а можно сказать, и дуга),синус которого равен х.
Слайд 4
Арксинус
Обозначение. Арксинус а обозначается arcsina.
Арксинусом числа а называется такое число
из отрезка

, синус которого равен а.
Очевидно, что а є [-1;1].
Т.к
Функция y=arcsin x- нечетная,
поэтому
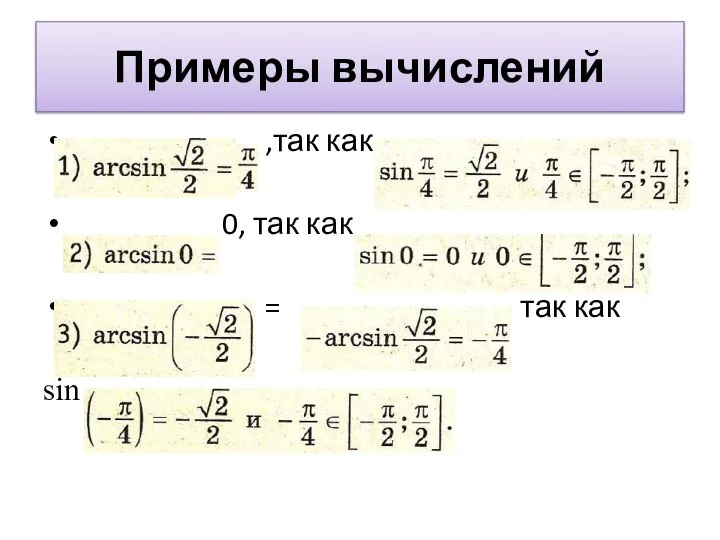
Слайд 5Примеры вычислений
,так как
0, так как
= , так как
sin
Слайд 6Арккосинус
Обозначение: Арккосинус а обозначается arccosa.
Арккосинусом числа а называется такое число из отрезка

, косинус которого равен а.
Очевидно, что а є [-1; 1]
Т.к.
Функция y=arccosx- четная,
поэтому
Слайд 8Арктангенс
Обозначение: Арктангенс а обозначается arctga.
Арктангенсом числа а называется такое число из интервала
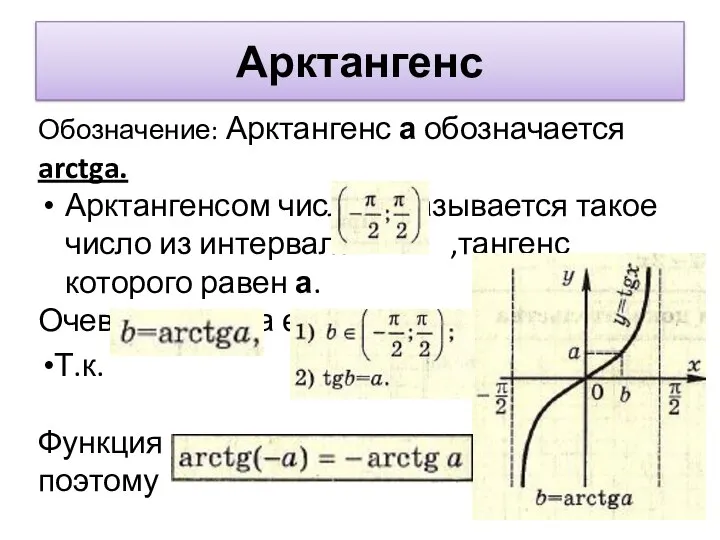
,тангенс которого равен а.
Очевидно, что а є (-∞; ∞)
Т.к.
Функция y=arctgx-нечетная,
поэтому
Слайд 10Арккотангенс
Обозначение: Арккотангенс а обозначается arcсtg a.
Арккотангенсом числа а называется такое число из интервала (0;?),котангенс

которого равен а.
Очевидно, что а є (-∞; ∞)
Т.к.
Функция y=arcctgx-нечетная,
поэтому
Слайд 12arcsin a, arcos a, arctg a, arcctg a-обратные тригонометрические функции
Функция обратная функции
Функция

обратная функции
Функция обратная функции
Функция обратная функции











 Уравнение сферы
Уравнение сферы Сумма углов треугольника
Сумма углов треугольника Решение систем уравнений способом подстановки
Решение систем уравнений способом подстановки Подготовка к ЕГЭ. Базовый и профильный уровни
Подготовка к ЕГЭ. Базовый и профильный уровни Презентация на тему Дифференцирование показательной и логарифмической функций
Презентация на тему Дифференцирование показательной и логарифмической функций  Односторонние пределы
Односторонние пределы Функция y = хх и её график
Функция y = хх и её график Сложение сил. Лабораторная работа №5
Сложение сил. Лабораторная работа №5 Поверхности и тела. Проецирование геометрических фигур
Поверхности и тела. Проецирование геометрических фигур Аксиомы планиметрии (часть 1)
Аксиомы планиметрии (часть 1) Решение задач
Решение задач Теорема, обратная теореме Пифагора
Теорема, обратная теореме Пифагора Задания на повторение курса алгебры (9 класс)
Задания на повторение курса алгебры (9 класс) Презентация на тему Решение логарифмических уравнений
Презентация на тему Решение логарифмических уравнений  аксіоми стереометрії
аксіоми стереометрії Подготовка к диагностической работе. 5 класс
Подготовка к диагностической работе. 5 класс ММК_Io66hWx
ММК_Io66hWx Свойство вертикальных углов
Свойство вертикальных углов Дроби. Математические гонки
Дроби. Математические гонки Логические функции
Логические функции Шкала отношений
Шкала отношений Презентация на тему Действия с многочленами
Презентация на тему Действия с многочленами  Рисуем с помощью координат
Рисуем с помощью координат Функции, их свойства и графики
Функции, их свойства и графики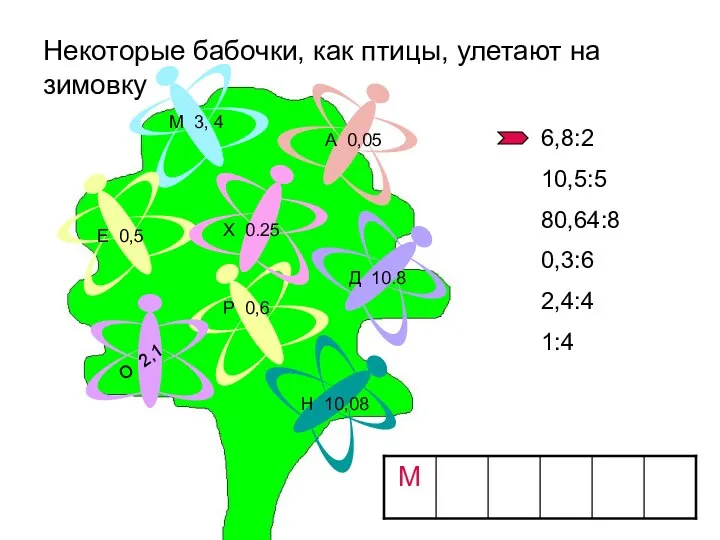 Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку
Устная работа (2). Некоторые бабочки, как птицы, улетают на зимовку Несобственные интегралы
Несобственные интегралы Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений Математический анализ
Математический анализ