Практическое применение теоремы косинусов и синусов. 9 класс

ПОВТОРЕНИЕ

ТЕОРЕМА СИНУСОВ
Стороны треугольника прямо пропорциональны синусам противолежащих углов.
Отношение стороны
треугольника к синусу
противолежащего угла
равно диаметру
описанной
окружности.
?

ПРИМЕР:

ТЕОРЕМА КОСИНУСОВ
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
а2 =b2 +c2 - 2bc cosA
Это частный
случай теоремы
Пифагора.
Почему?
?

ПРИМЕР:
Решение:

Практическое применение
теоремы косинусов и синусов

Решение.
Рассмотрим треугольник АВС, вершинами которого являются точка А расположения мяча и точки В и С в основаниях стоек ворот. По условию задачи с = АВ = 23 м, b = АС = 24 м и а = ВС = 7 м. Эти данные позволяют решить треугольник АВС и найти угол α, равный углу А. С помощью теоремы косинусов определяем cosA:
Угол α находим по таблице: α ≈ 16°57′.
Решение задачи №1
Условие.
Футбольный мяч находится в точке А футбольного поля на расстояниях 23 м и 24 м от оснований В и С стоек ворот (рис.1). Футболист направляет мяч в ворота. Найдите угол α попадания мяча в ворота, если ширина ворот равна 7 м.
1
1.

Предположим, что требуется определить высоту АН какого-либо предмета (рис. 2). Для этого отметим точку В на определенном расстоянии α от основания Н предмета и измерим угол АВН: ∠АВН=α. По этим данным из прямоугольного треугольника АВН находим высоту предмета: АН = а tgα.
Если основание предмета недоступно, то можно поступить так: на прямой, проходящей через основание Н предмета, отметим две точки В и С на определенном расстоянии α друг от друга и измерим углы АВН и АСВ: ∠АВН=α и ∠АСВ=β(рис. 2). Эти данные позволяют определить все элементы треугольника АВС, в частности АВ. В самом деле, ∠АВН- внешний угол треугольника АВС, поэтому ∠А=α-β.
Используя теорему синусов, находим АВ:
Из прямоугольного треугольника АВН находим высоту АН предмета:
АН=АВ⋅sin α. Итак, АН=
Решение задачи №2
Измерение высоты предмета

Предположим, что нам надо найти расстояние d от пункта А до недоступного пункта С (рис. 3). Напомним, что эту задачу мы уже решали в 8 классе с помощью признаков подобия треугольников. Рассмотрим теперь другой способ решения задачи – с использованием формул тригонометрии.
На местности выберем точку В и измерим длину с отрезка АВ. Затем измерим, например с помощью астролябии, углы А и В: ∠А=α и ∠В=β. Эти данные, т. е. с, α и β, позволяют решить треугольник АВС и найти искомое расстояние d=AC.
Сначала находим ∠С=180°-α-β,
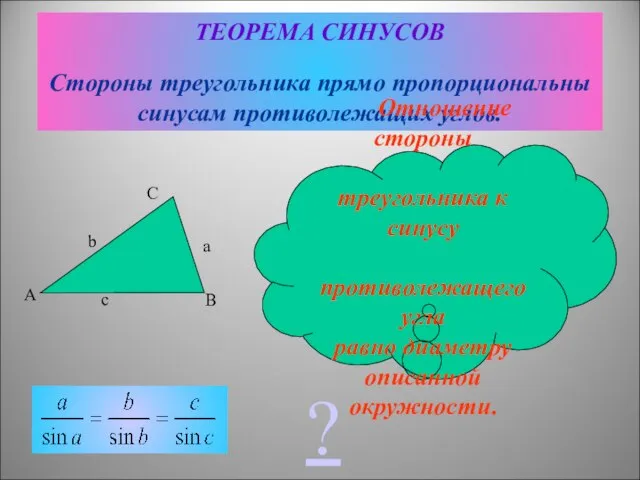
Sin С = sin(180°-α-β)=sin(α+β).
Затем с помощью теоремы синусов находим d. Так как ,
АС=d, AB=c, ∠B=β, то d= .
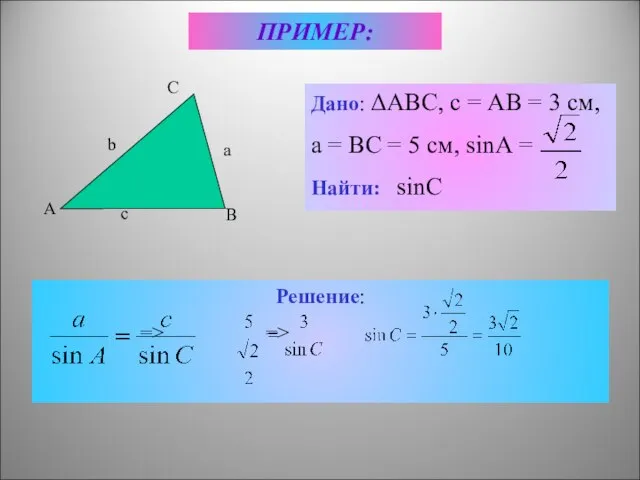
Решение задачи №3
Измерение расстояния до недоступной точки
3

Решите задачу №4
Для определения ширины реки отметили два пункта А и В на берегу реки на расстоянии 70 м друг от друга и измерили углы САВ и АВС, где С – дерево, стоящее на другом берегу у кромки воды. Оказалось, что ∠САВ=12°30′, ∠АВС=72°42′. Найдите ширину реки.
х
?

Решение задачи №4
∠C=180° - (∠A+∠B)
sin∠C = sin(∠A+∠B) = =sin(12°30'+72°42') = sin 85°12'
A
B
C
70 м
х
ОТВЕТ: Ширина реки равна 15,2 м.

Решите задачу №5
Наблюдатель находится на расстоянии 50 м от башни, высоту которой хочет определить. Основание башни он видит под углом 2° к горизонту, а вершину – под углом 45° к горизонту. Какова высота башни?
?

Решение задачи №5
1) АВКС - прямоугольник, ВК = АС = 50 м
2) △ ВDК: ∠В = 45°; ∠К = 90°, ∠D = 45° следовательно △ВDK равнобедренный,
т. е. ВК = DК = 50 м
3) △ВКС; ∠В=2°, ВК=50 м
∠С=180-(2+90)=88°
По теореме синусов
, то ;
м,
DС=50+2=52 м
ОТВЕТ:
Высота башни равна 52 м.