Понятия возрастающей и убывающей функций. Понятие монотонности функции. Возрастание и убывание функции

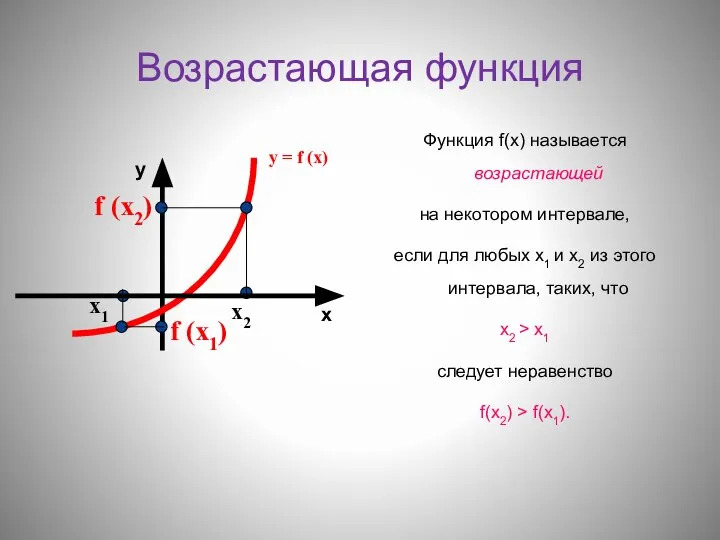
Возрастающая функция
Функция f(х) называется возрастающей
на некотором интервале,
если для любых х1 и х2 из этого интервала, таких, что
х2 > х1
следует неравенство
f(х2) > f(х1).
х
х1
х2
у
f (х1)
f (х2)
у = f (х)

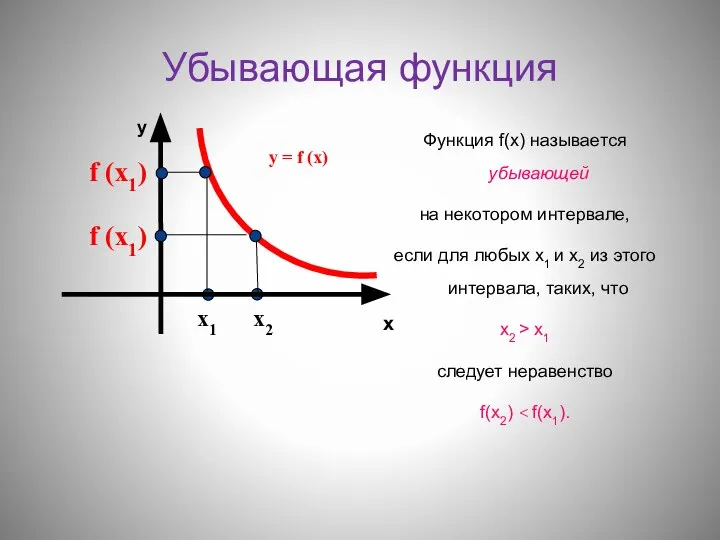
Убывающая функция
Функция f(х) называется убывающей
на некотором интервале,
если для любых х1 и х2 из этого интервала, таких, что
х2 > х1
следует неравенство
f(х2) < f(х1).
х
х1
х2
f (х1)
f (х1)
у = f (х)
у

Возрастающие и убывающие функции называются монотонными функциями.

Способы исследования функций на монотонность
Способ 1. По определению возрастающей (убывающей) функции.
Способ 2. По графику функции.

Пример №1. Исследуйте функцию f(x)= 1/х на
монотонность.
Решение.
D(f) : х ≠ 0
Пусть х2 и x1 - произвольные точки из D(f) такие, что х2 > x1 , тогда f(x2) - f(x1) = 1/x2 – 1/ x1 = (х1 –х2)/ х2 х1 < 0, значит данная функция убывает на каждом из двух промежутков своей области определения.

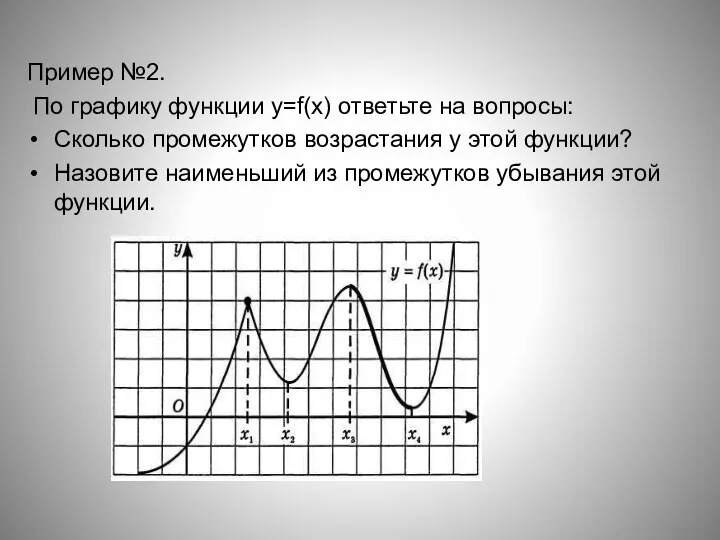
Пример №2.
По графику функции y=f(x) ответьте на вопросы:
Сколько промежутков возрастания у этой функции?
Назовите наименьший из промежутков убывания этой функции.

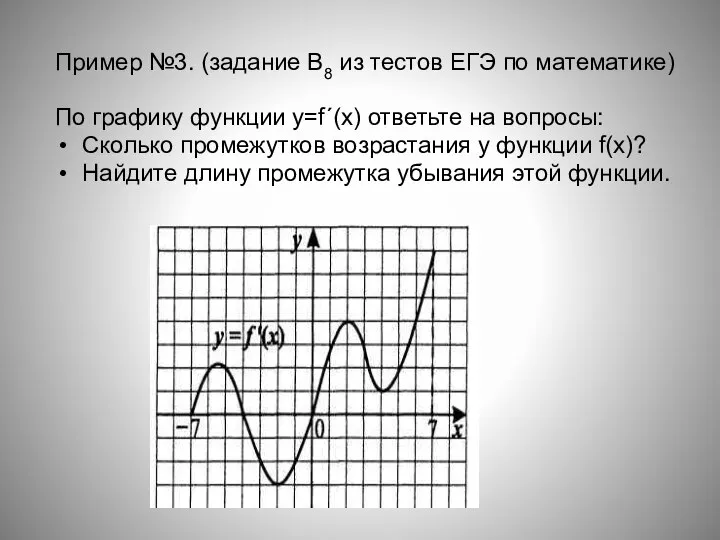
Пример №3. (задание В8 из тестов ЕГЭ по математике)
По графику функции y=f´(x) ответьте на вопросы:
Сколько промежутков возрастания у функции f(x)?
Найдите длину промежутка убывания этой функции.

Наши цели
1. Найти связь между производной и свойством монотонности функции.
2. Создать алгоритм поиска промежутков монотонности функции с помощью производной.

Тема урока:
«Возрастание и убывание функции»

Гипотеза
Если f/(x) > 0 на некотором интервале, то функция возрастает на этом интервале.
Если f/(x) < 0 на некотором интервале, то функция убывает на этом интервале.

Достаточный признак возрастания(убывания) функции

№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания функции.

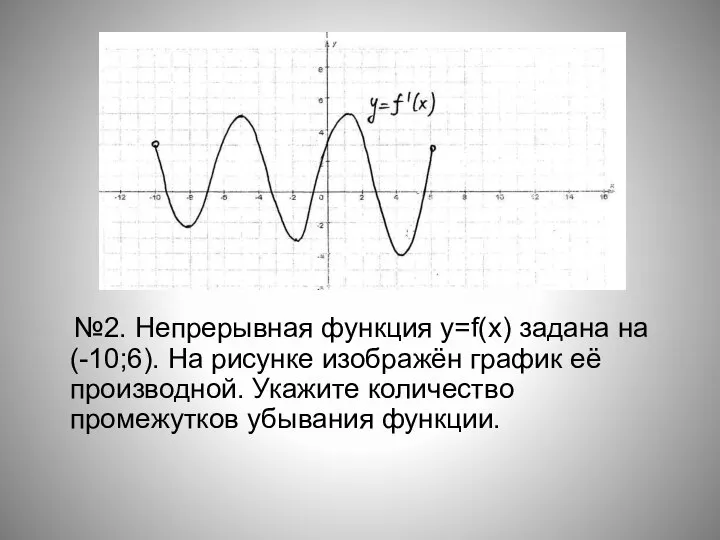
№2. Непрерывная функция y=f(x) задана на (-10;6). На рисунке изображён график её производной. Укажите количество промежутков убывания функции.

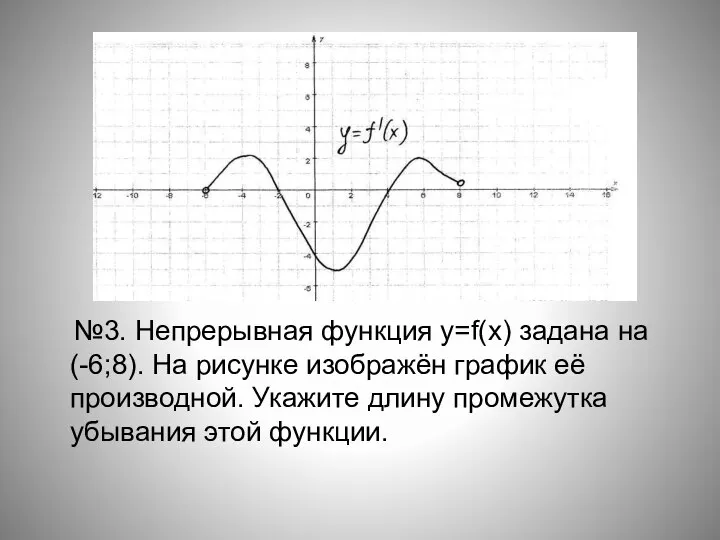
№3. Непрерывная функция y=f(x) задана на (-6;8). На рисунке изображён график её производной. Укажите длину промежутка убывания этой функции.

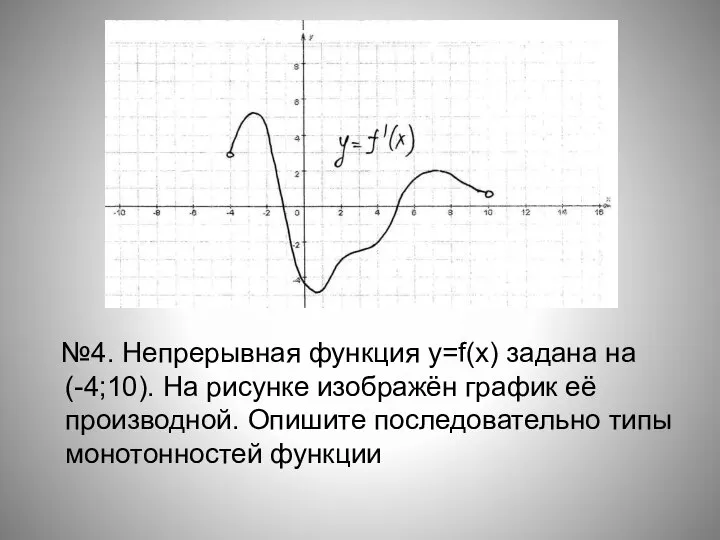
№4. Непрерывная функция y=f(x) задана на (-4;10). На рисунке изображён график её производной. Опишите последовательно типы монотонностей функции

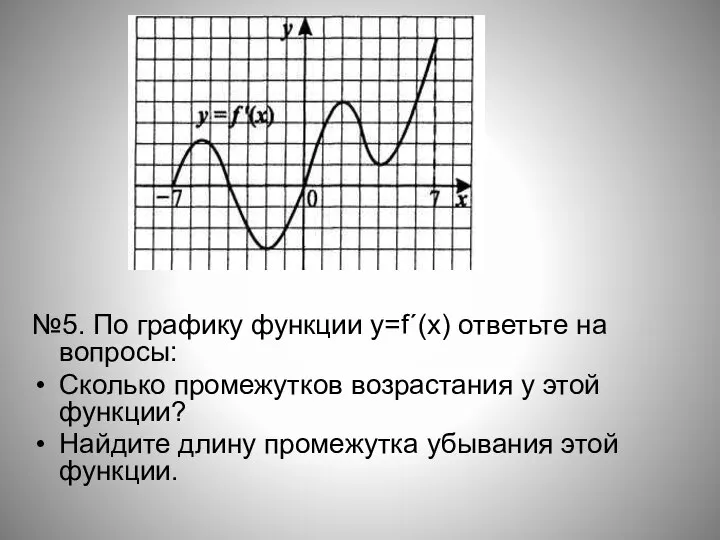
№5. По графику функции y=f´(x) ответьте на вопросы:
Сколько промежутков возрастания у этой функции?
Найдите длину промежутка убывания этой функции.

Алгоритм
1. Указать область определения функции.
2. Найти производную функции.
3. Определить промежутки, в которых
f/(x) > 0 и f/(x) < 0.
4. Сделать выводы о монотонности
функции.

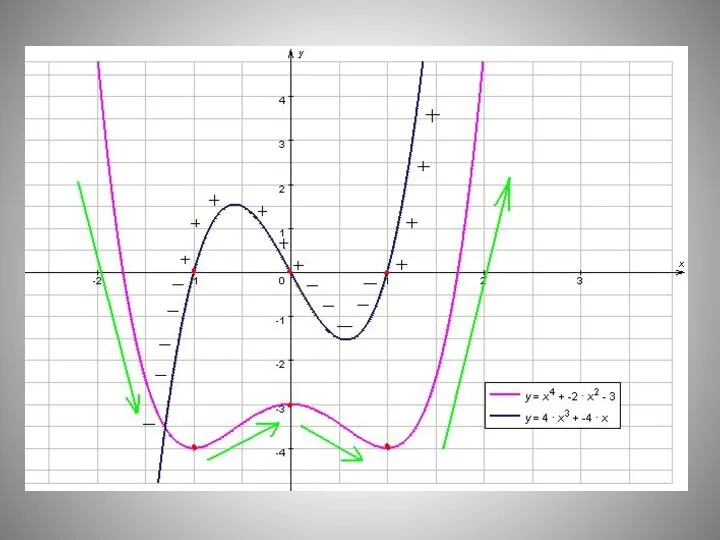
Образец решения по алгоритму
f(х) = х4 - 2х2 ,
1. D(f) = R
2. f/(x) = 4х3 - 4х,
3. f/(x)>0, если 4х3 - 4х >0, х3 - х >0, х(х-1)(х+1)>0
-1 0 1 х
f/(x): - + - +
f(х):
4. Функция убывает на промежутках (-∞;-1)] и [(0; 1)] .
Функция возрастает на промежутках [(-1; 0)] и [(1; + ∞)]