Содержание
- 2. Классическое определение предела функции на языке «Эпсилон-Дельта» Пусть функция y = f(x) определена в некоторой окрестности
- 3. Основные теоремы о пределах Рассмотрим теоремы, которые облегчают нахождение пределов функций. Предел суммы (разности) двух функций
- 4. Основные теоремы о пределах Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя
- 5. Способы вычисления пределов Непосредственной подстановкой. Разложение числителя и знаменателя на множители и сокращение дроби. Умножение на
- 6. Вычисление пределов Вычисление предела: начинают с подстановки предельного значения x0 в функцию f(x). Если при этом
- 10. Вычисление пределов Часто при подстановке получаются выражения следующих видов: Эти выражения называются неопределенности, а вычисление пределов
- 12. Скачать презентацию









 Определители. Свойство определителей
Определители. Свойство определителей Оцінки типу Височанського-Петуніна в класі чистих неперервних типів розподілів
Оцінки типу Височанського-Петуніна в класі чистих неперервних типів розподілів Прямі і площини в просторі
Прямі і площини в просторі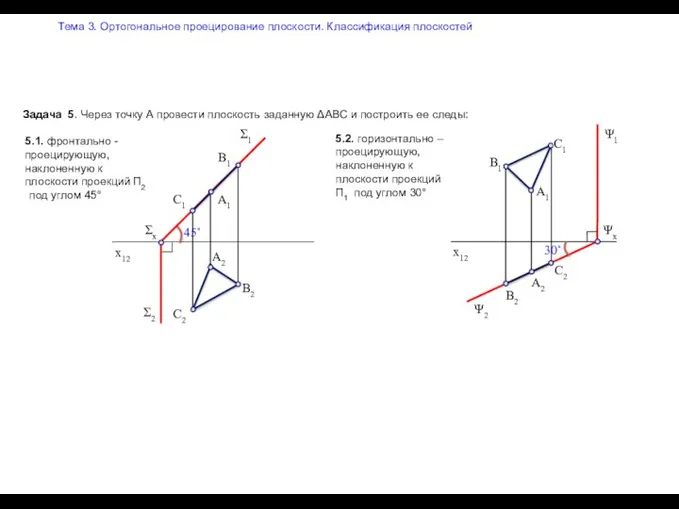 Ортогональное проецирование плоскости. Классификация плоскостей
Ортогональное проецирование плоскости. Классификация плоскостей Логарифмы. Задания В7, В11 на ЕГЭ
Логарифмы. Задания В7, В11 на ЕГЭ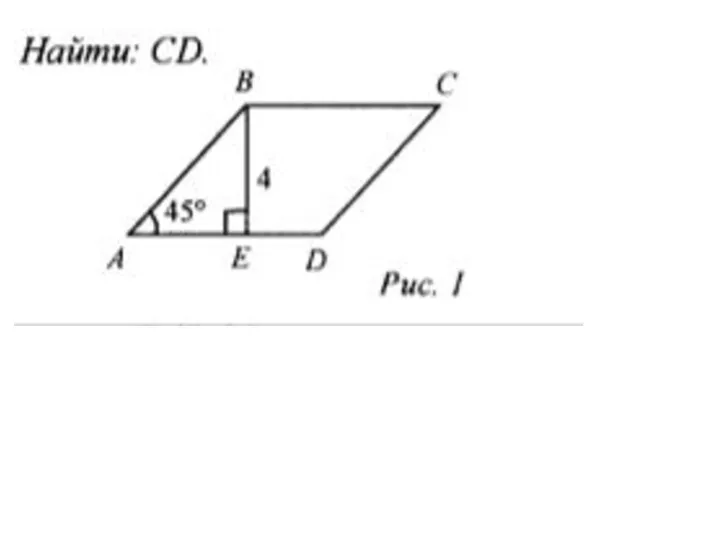 Вычисление площадей
Вычисление площадей Математическое моделирование. Рандомизация
Математическое моделирование. Рандомизация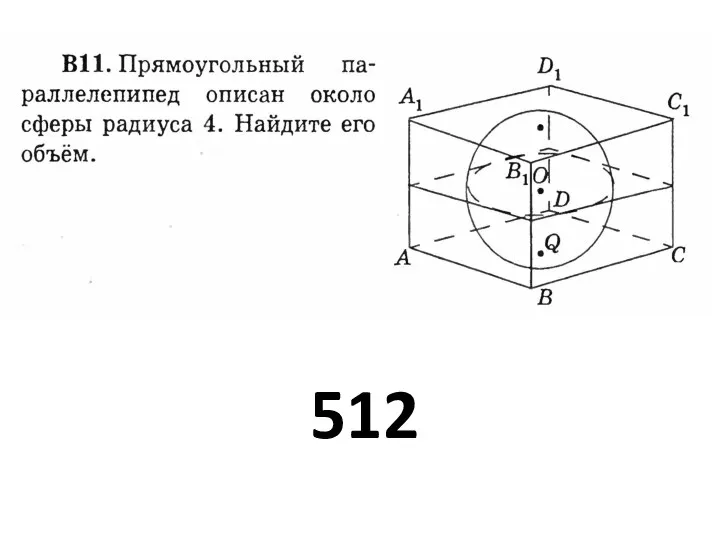 Решение задач по геометрии
Решение задач по геометрии Теорема о свойстве биссектрисы с доказательством
Теорема о свойстве биссектрисы с доказательством Числовые ряды
Числовые ряды Свойство и признак описанного четырёхугольника
Свойство и признак описанного четырёхугольника Тест на основе шаблона Баженова А. А
Тест на основе шаблона Баженова А. А Задания на повторение курса алгебры (9 класс)
Задания на повторение курса алгебры (9 класс) Задания для домашнего обучения
Задания для домашнего обучения Методы и приемы решения дробно-рациональных уравнений, содержащих параметр
Методы и приемы решения дробно-рациональных уравнений, содержащих параметр Расстояние от точки до прямой. Решение задач
Расстояние от точки до прямой. Решение задач Первый признак подобия треугольников. Решение задач
Первый признак подобия треугольников. Решение задач Формулы сокращенного умножения. Разность квадратов
Формулы сокращенного умножения. Разность квадратов Решение задач и неравенств
Решение задач и неравенств комбинаторика 1 лекция-1
комбинаторика 1 лекция-1 Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)
Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)  Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы
Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы Операции с числовыми множествами. Формулы сокращённого умножения
Операции с числовыми множествами. Формулы сокращённого умножения Деление целых чисел
Деление целых чисел Тригонометрические уравнения, сводящиеся к квадратным
Тригонометрические уравнения, сводящиеся к квадратным Прямоугольник. Квадрат. Периметр многоугольника
Прямоугольник. Квадрат. Периметр многоугольника Своя игра (2)
Своя игра (2) Корни n-й степени и их свойства
Корни n-й степени и их свойства