Predel_funktsii_v_tochke

Предел функции
Работайте, работайте, - полное понимание придет потом.
Даламбер

Предел функции в точке
Пусть функция y = f(x) определена в некоторой окрестности точки x0, кроме, быть может самой точки x0.

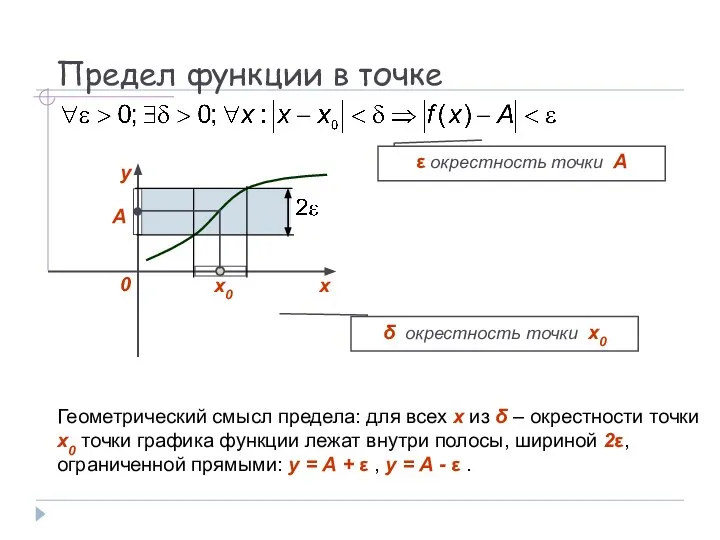
Предел функции в точке
х0
А
δ окрестность точки x0
ε окрестность точки А
Геометрический смысл предела: для всех х из δ – окрестности точки x0 точки графика функции лежат внутри полосы, шириной 2ε, ограниченной прямыми: у = А + ε , у = А - ε .

Коши Огюстен Луи
Коши Огюстен Луи (1789–1857), французский математик. Работал в Шербуре инженером, преподавал в Политехнической школе, Сорбонне и Коллеж де Франс.
Работы Коши посвящены арифметике, теории чисел, алгебре, математическому анализу, дифференциальным уравнениям, механике, математической физике. Коши впервые дал четкое определение пределу, непрерывности функции, сходимости ряда и т.д

Односторонние пределы
В определении предела функции
Бывают случаи, когда способ приближения аргумента x к x0 существенно влияет на значение предела, поэтому вводят понятия односторонних пределов.
предполагается, что x стремится к x0 любым способом: оставаясь меньше, чем x0 (слева от x0), большим, чем x0 (справа от x0), или колеблясь около точки x0.
Число А1 называют пределом функции слева в точке x0, если для любого ε > 0 найдется такое δ >0, что для всех справедливо неравенство:
Предел слева записывают так:

Односторонние пределы
Число А2 называют пределом функции справа в точке x0, если
Предел справа записывают так:
А1
х0
А2
Пределы функции слева и справа называют односторонними пределами.
Очевидно, если существует
то существуют и оба односторонних предела, причем А = А1 = А2

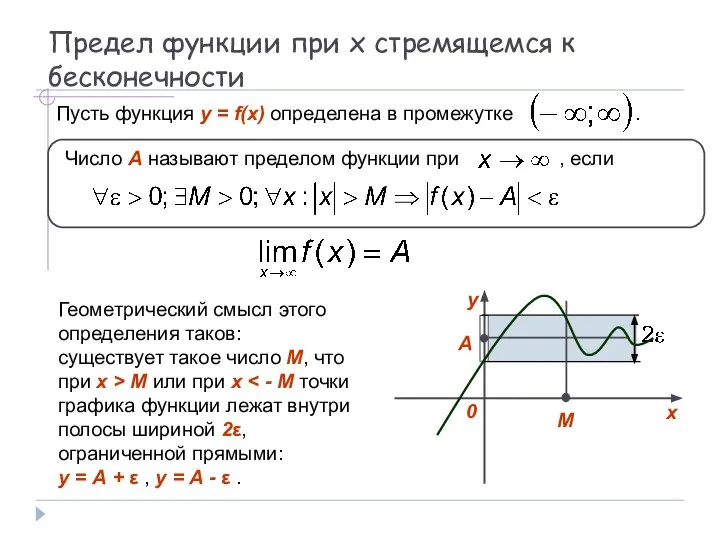
Предел функции при x стремящемся к бесконечности
Пусть функция y = f(x) определена в промежутке .
Число А называют пределом функции при , если
Геометрический смысл этого определения таков:
существует такое число М, что при х > M или при x < - M точки графика функции лежат внутри полосы шириной 2ε, ограниченной прямыми:
у = А + ε , у = А - ε .
М
А

Основные теоремы о пределах
Рассмотрим теоремы, которые облегчают нахождение пределов функций.
Предел суммы (разности) двух функций равен сумме (разности) пределов:
Предел произведения двух функций равен произведению пределов:
Постоянный множитель можно выносить за знак предела:

Основные теоремы о пределах
Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:
Предел степени с натуральным показателем равен той же степени предела:
Предел показательно – степенной функции:

Основные теоремы о пределах
Если между соответствующими значениями трех функций
при этом:
тогда:
выполняются неравенства:
Если функция f(x) монотонна и ограничена при x < x0 или при
x > x0, то существует соответственно ее левый предел:
или ее правый предел:

Бесконечно малые функции
Функция f(x) называется бесконечно малой при х->x0, если
.
Обозначение: α, β, γ и т.д.
Функция f(x) называется бесконечно большой при х->x0, если
Связь между б.м. и б.б.
Если есть б.м. , то б.б.
Если есть б.б., то б.м.

Свойства бесконечно малых.
Теорема 1. Если функция f(x) имеет предел при х->x0, равный А, то она представима в виде
f(x) = А + α(х) , где α(х) – б.м.ф.
Справедливо и обратное: если функция f(x) представима равенством f(x) = А + α(х) при х->x0, то её предел равен А.
Теорема 2. Алгебраическая сумма конечного числа бесконечно малых в точке функций есть бесконечно малая функция

Теорема 3. Произведение ограниченной при функции на бесконечно малую есть бесконечно малая функция.
Следствие 1. Произведение постоянной величины на бесконечно малую есть функция бесконечно малая.
Следствие 2. Произведение конечного числа бесконечно малых функций есть функция бесконечно малая

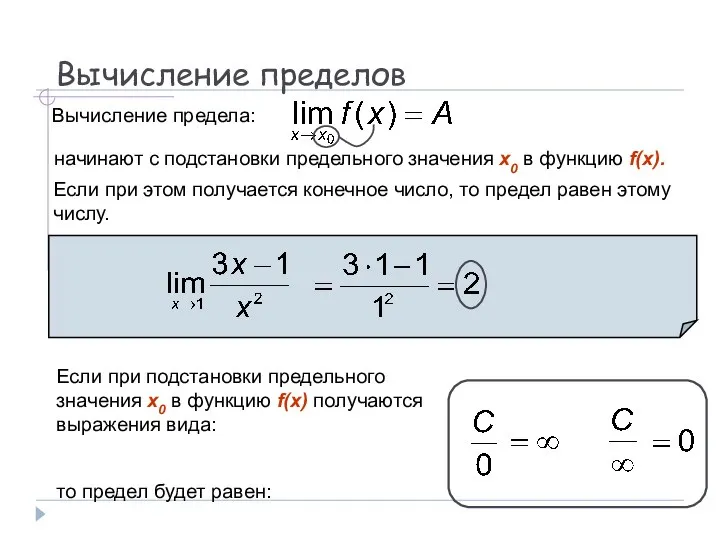
Вычисление пределов
Вычисление предела:
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому числу.
Если при подстановки предельного значения x0 в функцию f(x) получаются выражения вида:
то предел будет равен:

Вычисление пределов
Часто при подстановке предельного значения x0 в функцию f(x) получаются выражения следующих видов:
Эти выражения называются неопределенности, а вычисление пределов в этом случае называется раскрытие неопределенности.

Раскрытие неопределенностей
Раскрытие неопределенности
Если f(x) – дробно – рациональная функция, необходимо разложить на множители числитель и знаменатель дроби
Если f(x) – иррациональная дробь, необходимо умножить числитель и знаменатель дроби на выражение, сопряженное числителю.

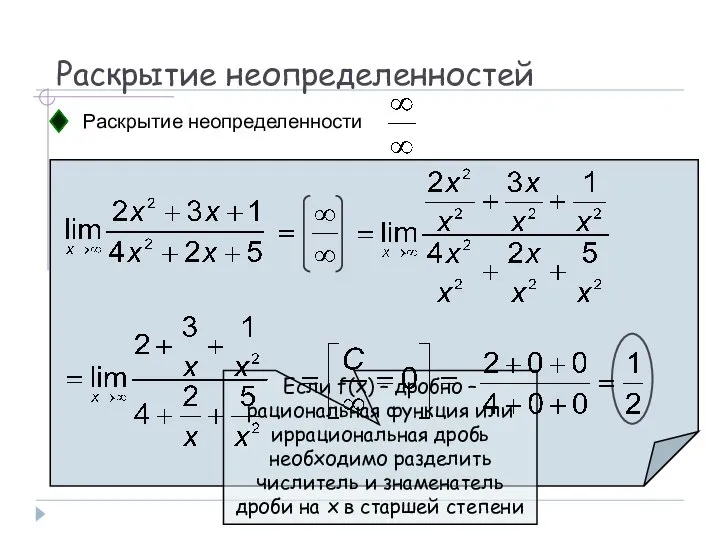
Раскрытие неопределенностей
Раскрытие неопределенности
Если f(x) – дробно – рациональная функция или иррациональная дробь необходимо разделить числитель и знаменатель дроби на x в старшей степени

Раскрытие неопределенностей
Раскрытие неопределенности
Умножим и разделим функцию на сопряженное выражение.

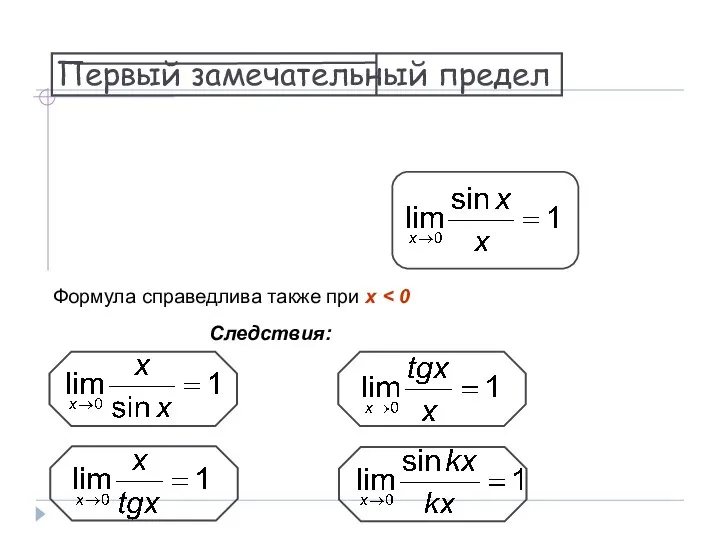
Первый замечательный предел
Следствия:
Формула справедлива также при x < 0

Первый замечательный предел

Второй замечательный предел
Вторым замечательным пределом называется равенство:
Следствия:
Другие полезные формулы: