Организация поисковой и рефлексивной деятельности учащихся при решении планиметрических задач. ГИА 2013. Задачи №23
Содержание
- 2. Цели занятия: Показать различные приемы решения планиметрических задач. 2. Показать, как организовать поисковую и рефлексивную деятельность
- 3. Этапы работы над планиметрической задачей: 1. Построение чертежа и нанесение всех данных задачи. 2. Поиск способа
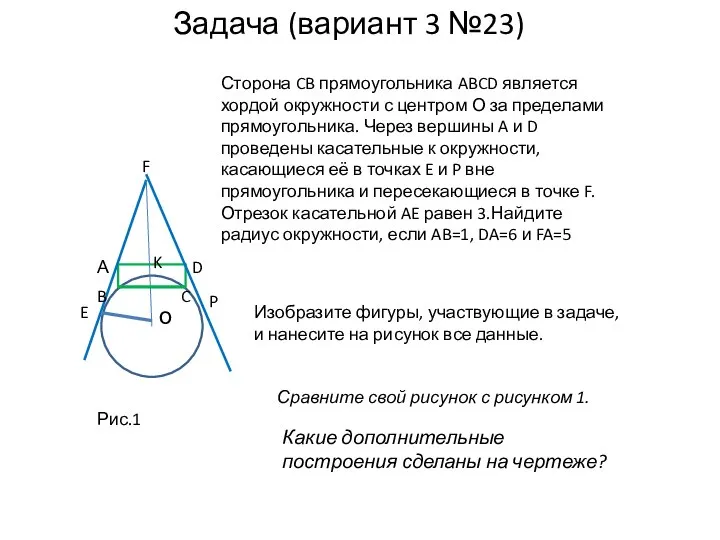
- 4. Задача (вариант 3 №23) Сторона CB прямоугольника ABCD является хордой окружности с центром О за пределами
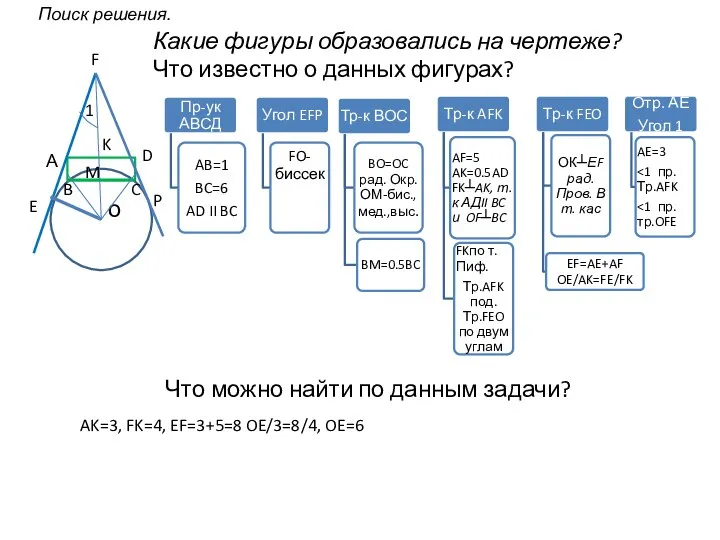
- 5. о C B А F E K D P M Поиск решения. Какие фигуры образовались на
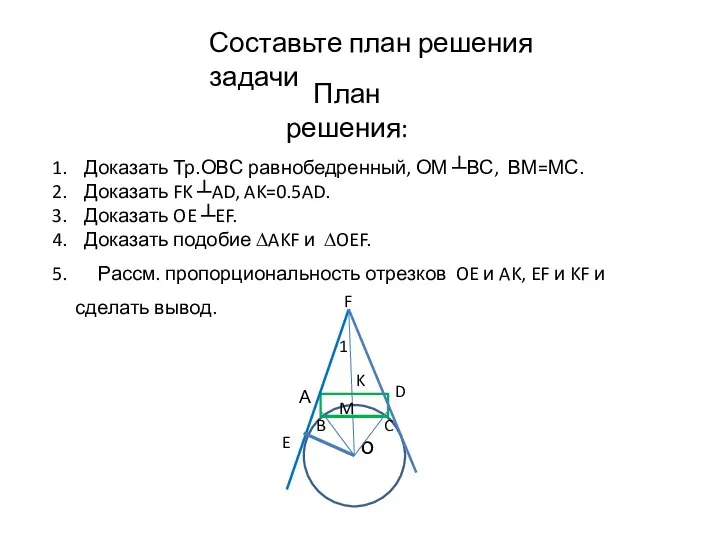
- 6. Составьте план решения задачи План решения: Доказать Тр.ОВС равнобедренный, ОМ ┴ВС, ВМ=МС. Доказать FK ┴AD, AK=0.5AD.
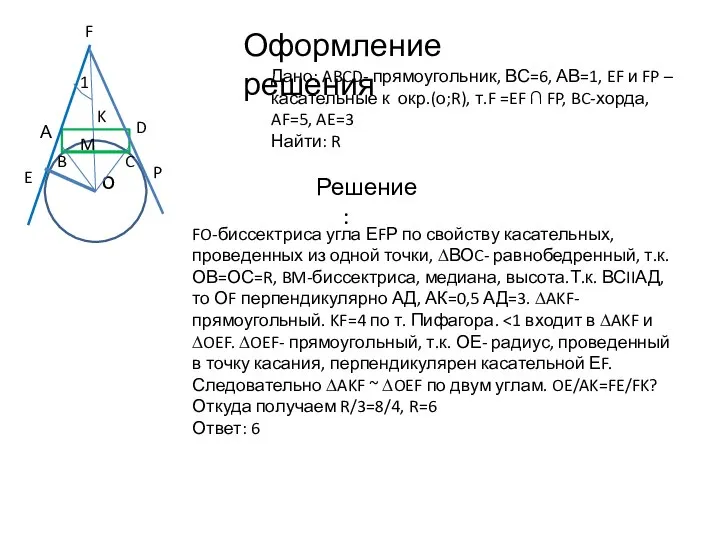
- 7. Оформление решения Дано: ABCD- прямоугольник, ВС=6, АВ=1, EF и FP – касательные к окр.(о;R), т.F =EF
- 8. Подведение итогов. Какие сведения из курса планиметрии потребовались для решения задачи? 2. Сгруппируйте теоретические сведения по
- 9. «Треугольник»: Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой треугольника. Если два угла одного
- 11. Скачать презентацию




 Проценты
Проценты Тест по теме функция
Тест по теме функция Презентация на тему Четырехугольники вокруг нас
Презентация на тему Четырехугольники вокруг нас  Задачи о наполнении сосуда
Задачи о наполнении сосуда Тригонометрические неравенства Слайды для урока по теме:
Тригонометрические неравенства Слайды для урока по теме: Приемы решения целых уравнений
Приемы решения целых уравнений Алгоритм вычисления площади с помощью палетки
Алгоритм вычисления площади с помощью палетки Виды движения в работах Эшера
Виды движения в работах Эшера Геометрическая прогрессия. Урок 3
Геометрическая прогрессия. Урок 3 Геометрический материал
Геометрический материал Усечённая пирамида
Усечённая пирамида Ответы к тестам для подготовки к ЕГЭ по математике
Ответы к тестам для подготовки к ЕГЭ по математике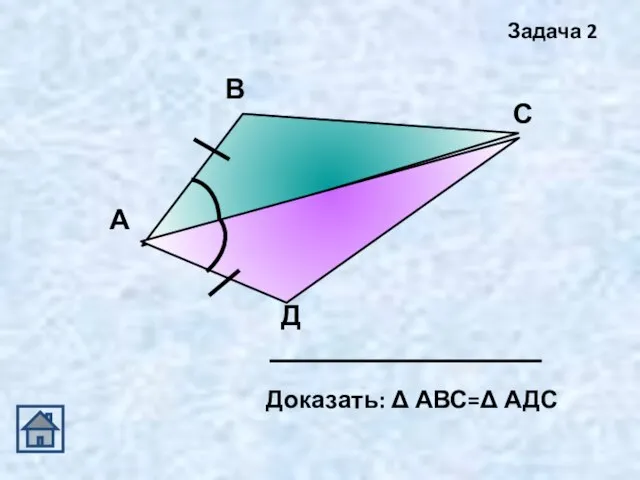 Первый признак равенства треугольника
Первый признак равенства треугольника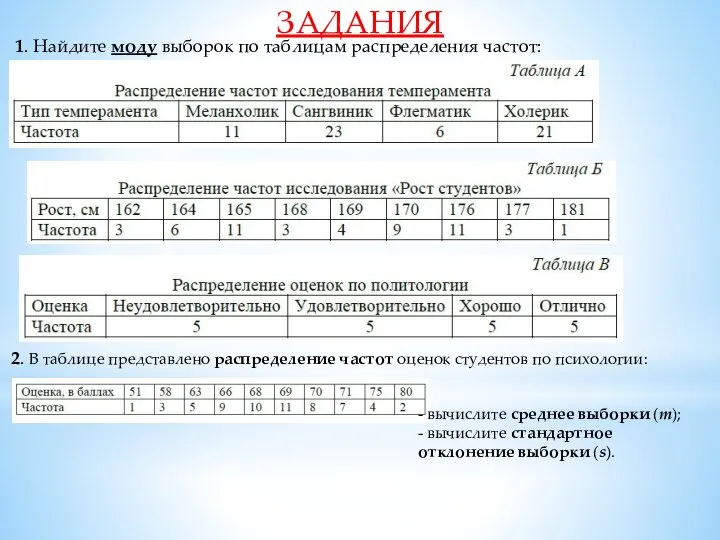 Математические методы
Математические методы Тема 1
Тема 1 Построение сечений многогранников
Построение сечений многогранников Статические таблицы
Статические таблицы Числа Фибоначчи
Числа Фибоначчи Твёрдые и мягкие согласные звуки. Сложение и вычитание без перехода через десяток
Твёрдые и мягкие согласные звуки. Сложение и вычитание без перехода через десяток Вариационные ряды
Вариационные ряды Счастливый случай. Урок- зачет по подготовке к ГИА
Счастливый случай. Урок- зачет по подготовке к ГИА Эмпирико-статистические модели климатических изменений. Земля как климатическая система
Эмпирико-статистические модели климатических изменений. Земля как климатическая система Уравнения, приводимые к квадратным
Уравнения, приводимые к квадратным Буквенные выражения. Подготовка к контрольной работе
Буквенные выражения. Подготовка к контрольной работе Равносильность формул
Равносильность формул Треугольники (элементы, площади)
Треугольники (элементы, площади) Признаки подобия треугольника
Признаки подобия треугольника Решение задания 12 ЕГЭ (профиль)
Решение задания 12 ЕГЭ (профиль)