Содержание
- 2. ГРАФЫ Графами называются геометрические фигуры, состоящие из точек (вершин графа) и линий (ребер графа), соединяющих эти
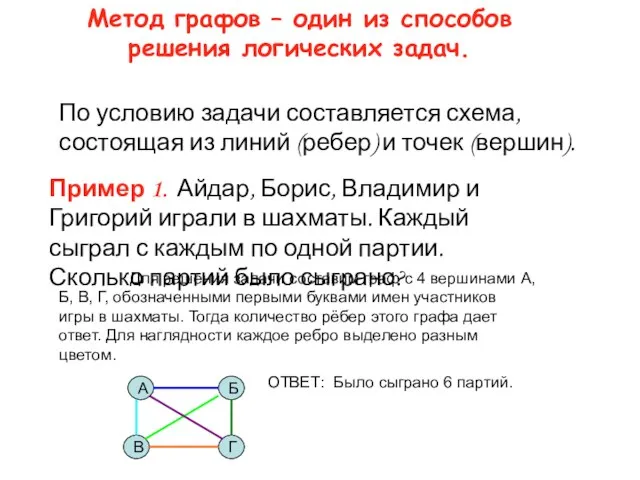
- 3. Метод графов – один из способов решения логических задач. По условию задачи составляется схема, состоящая из
- 4. Используя метод графов, решите задачу самостоятельно. Пять приятелей при встрече пожали друг другу руки. Сколько всего
- 5. Прием моделирования с помощью графов. Ситуации, в которых требуется найти соответствие между элементами различных множеств, можно
- 6. Три товарища –Иван, Дмитрий и Степан преподают различные предметы (химию, биологию и физику) в школах Москвы
- 7. В задаче можно выделить три множества: учебных предметов, городов, учителей. Каждое множество содержит по три элемента.
- 8. По условию задачи будем соединять точки отрезками (сплошными линиями), если имеет место соответствие между данными элементами,
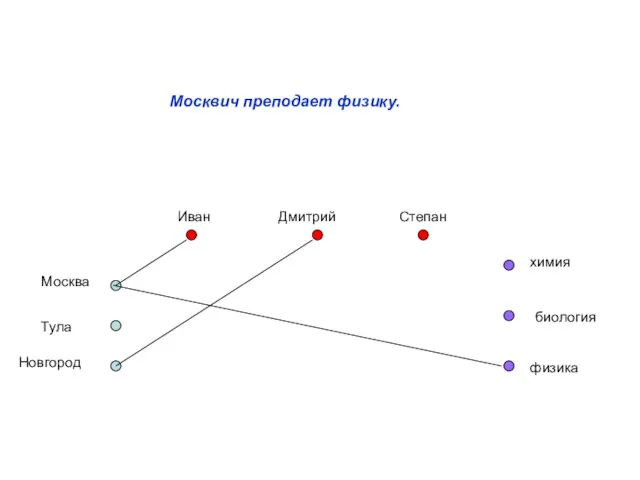
- 9. Москвич преподает физику.
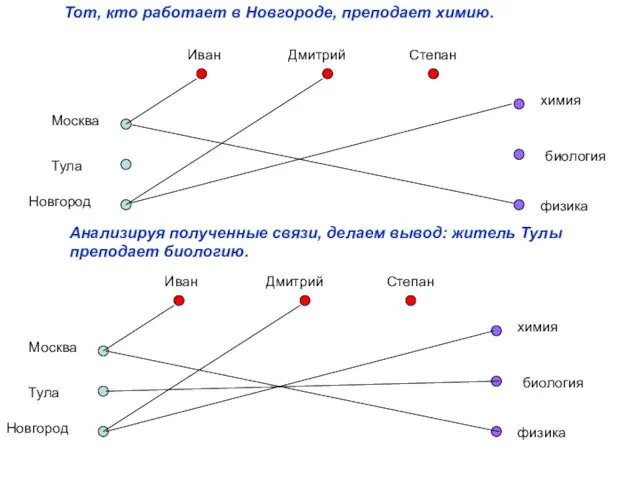
- 10. Анализируя полученные связи, делаем вывод: житель Тулы преподает биологию. Тот, кто работает в Новгороде, преподает химию.
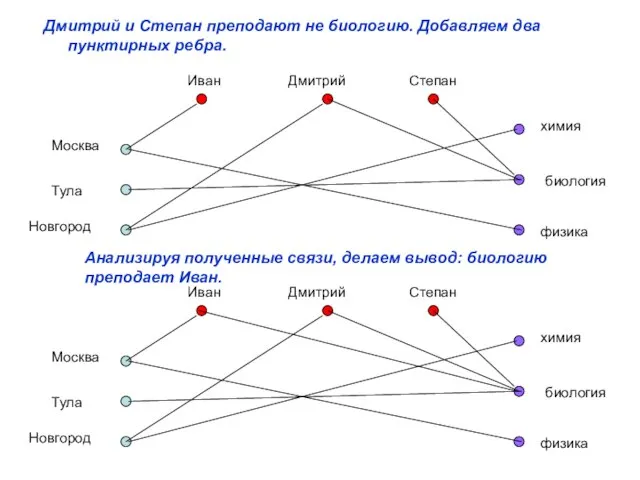
- 11. Дмитрий и Степан преподают не биологию. Добавляем два пунктирных ребра. Анализируя полученные связи, делаем вывод: биологию
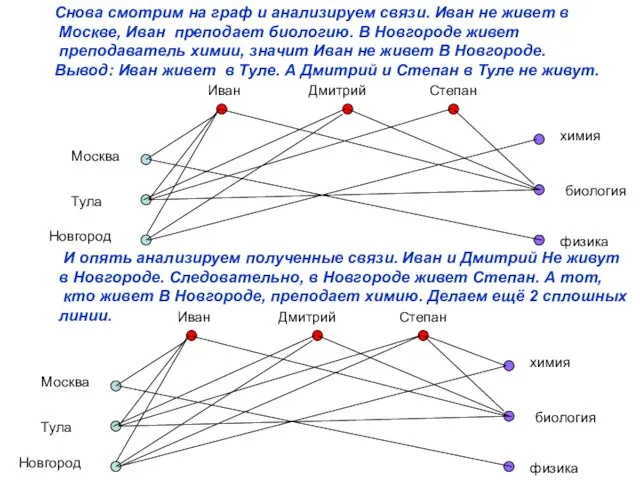
- 12. Снова смотрим на граф и анализируем связи. Иван не живет в Москве, Иван преподает биологию. В
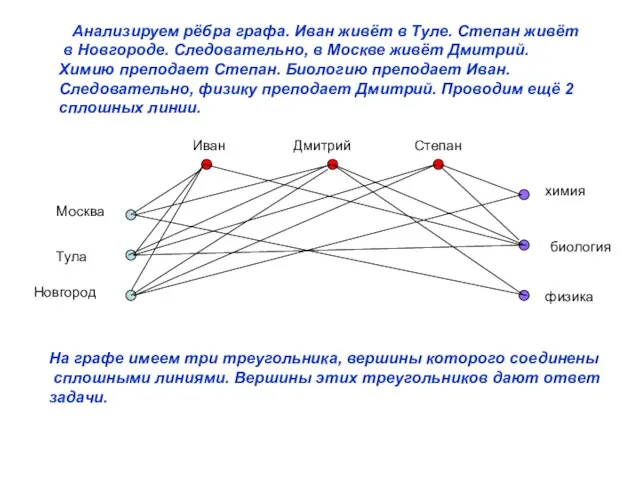
- 13. Анализируем рёбра графа. Иван живёт в Туле. Степан живёт в Новгороде. Следовательно, в Москве живёт Дмитрий.
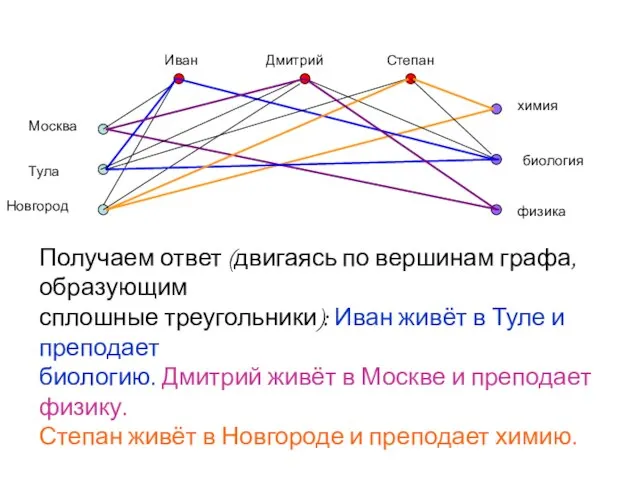
- 14. Получаем ответ (двигаясь по вершинам графа, образующим сплошные треугольники): Иван живёт в Туле и преподает биологию.
- 16. Скачать презентацию






 Площадь боковой поверхности тела вращения. Лекция №11
Площадь боковой поверхности тела вращения. Лекция №11 Цепочки. Сравните выражения
Цепочки. Сравните выражения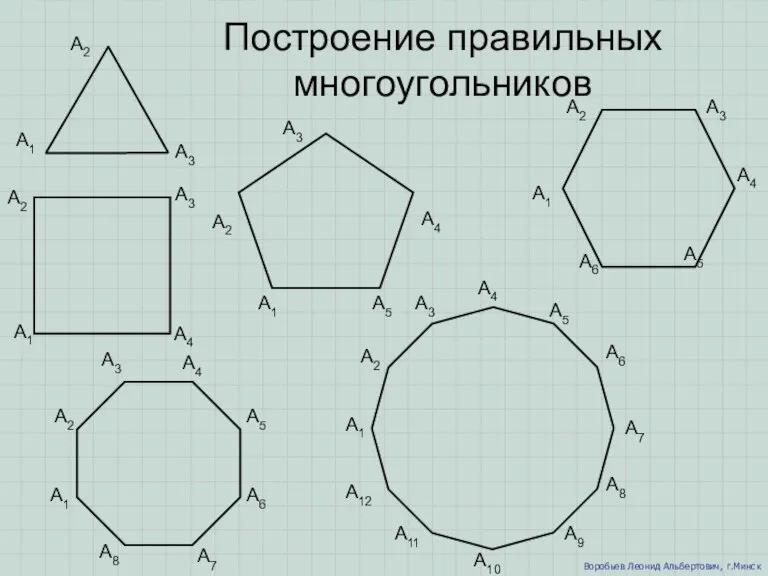 Построение правильных многоугольников
Построение правильных многоугольников Комплексные числа и квадратные уравнения
Комплексные числа и квадратные уравнения Найди фигуру (развиваем логику)
Найди фигуру (развиваем логику) Закрепление знаний. Страничка для любознательных
Закрепление знаний. Страничка для любознательных Эквивалентные бесконечно малые функции
Эквивалентные бесконечно малые функции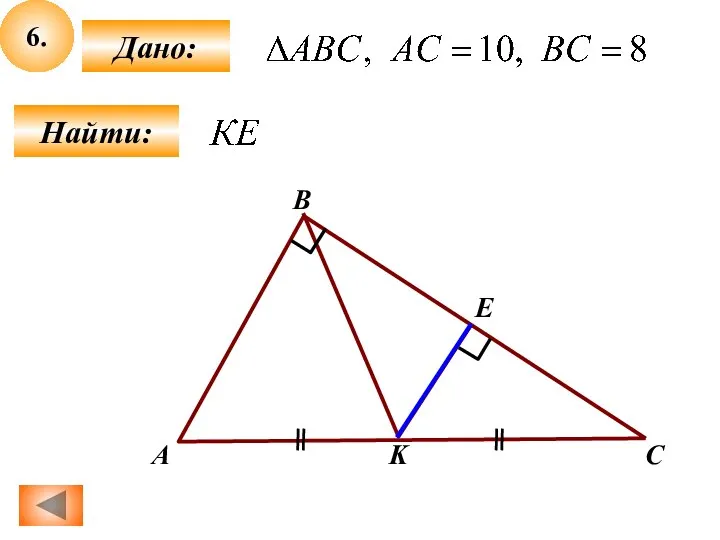 Задачи по геометрии (6-7)
Задачи по геометрии (6-7) Презентация на тему Деление десятичных дробей
Презентация на тему Деление десятичных дробей  Проценты
Проценты Экстремумы функции
Экстремумы функции История зарождения и развития геометрии
История зарождения и развития геометрии Число 8
Число 8 Чтение графика функции
Чтение графика функции Степень с рациональным показателем. Множество рациональных чисел
Степень с рациональным показателем. Множество рациональных чисел Функция у=1/х и её график
Функция у=1/х и её график Математические основы криптографии
Математические основы криптографии 6a04a5dd-75c3-461b-a240-737df2a5d137
6a04a5dd-75c3-461b-a240-737df2a5d137 Алгебра логики
Алгебра логики Математическое моделирование. Основные положения
Математическое моделирование. Основные положения Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого Комбинаторные задачи. 9 класс
Комбинаторные задачи. 9 класс Решение задач на оптимизацию методами математического анализа
Решение задач на оптимизацию методами математического анализа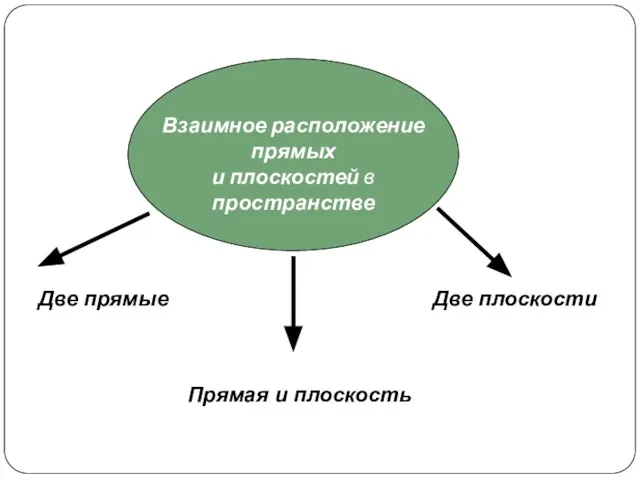 Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве Графическое и табличное представление информации
Графическое и табличное представление информации Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ
Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ  Сложение чисел. Тренажер, 1 класс
Сложение чисел. Тренажер, 1 класс