+ 3у = 0.
Графиком является прямая, проходящая через точки (0; 0) и (-6; 4).
х
у
1
-6
4
Так как неравенство строгое, координаты точек графика не являются его решением, поэтому прямую строим пунктирной линией.
Прямая разбила плоскость на две полуплоскости.
Все решения неравенства геометрически изображены точками одной из полуплоскостей.
Чтобы выбрать нужную полуплоскость, подставим координаты произвольной точки в исходное неравенство.
1
3
Возмем точку (3; 1).
Получаем: 2·3 + 3·1 > 0 – верно, значит все решения исходного неравенства геометрически изображены точками, расположенными в верхней полуплоскости.
.










 Случайные события
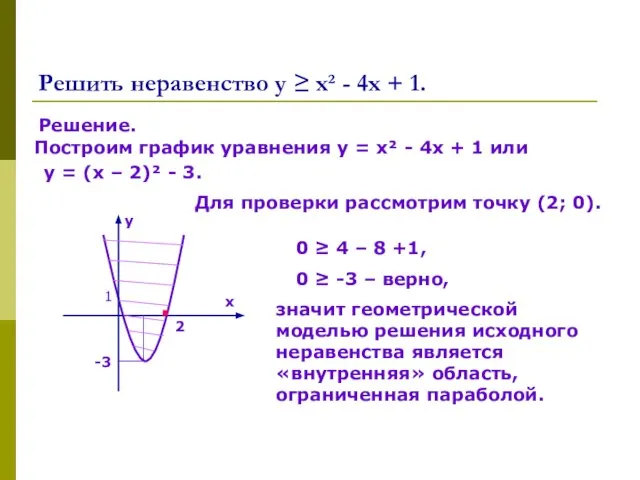
Случайные события Решите неравенства
Решите неравенства Параллельность прямых и плоскостей в пространстве с решением
Параллельность прямых и плоскостей в пространстве с решением Свойства функций. 9 класс
Свойства функций. 9 класс Интересные факты про математику
Интересные факты про математику Скалярное произведение векторов. тест
Скалярное произведение векторов. тест Подготовка к контрольной работе. Изображение промежутков и запись их в виде неравенств
Подготовка к контрольной работе. Изображение промежутков и запись их в виде неравенств Математические головоломки. Математика вокруг нас
Математические головоломки. Математика вокруг нас Признаки параллелограмма
Признаки параллелограмма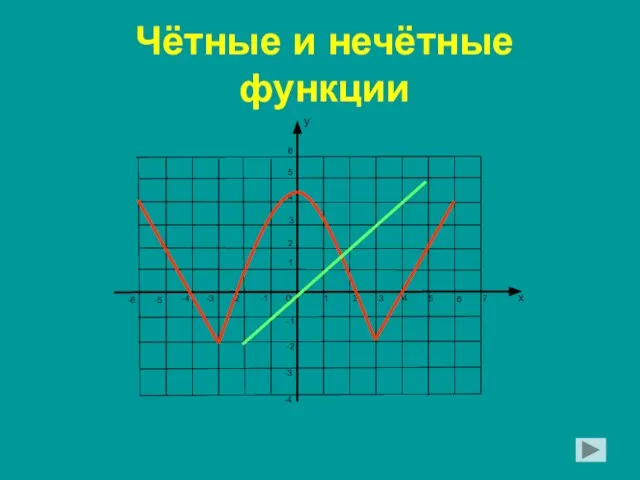 Презентация на тему Чётные и нечётные функции
Презентация на тему Чётные и нечётные функции  Решение треугольников. 9 класс
Решение треугольников. 9 класс Правильные многогранники. Моделирование многогранников
Правильные многогранники. Моделирование многогранников Угол между прямой и плоскостью
Угол между прямой и плоскостью Подобие треугольников. Второй признак
Подобие треугольников. Второй признак Дробь. Подготовка к олимпиадам
Дробь. Подготовка к олимпиадам Равносильные преобразования
Равносильные преобразования Задача по математике (4 класс, задание 85.1)
Задача по математике (4 класс, задание 85.1) Музыкалық аспаптарға
Музыкалық аспаптарға Пределы
Пределы Выражение в инфиксной форме. Выражение в постфиксной форме
Выражение в инфиксной форме. Выражение в постфиксной форме Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Математическое и сенсорное развитие детей раннего возраста
Математическое и сенсорное развитие детей раннего возраста Применение функциональных зависимостей в реальных процессах и явлениях
Применение функциональных зависимостей в реальных процессах и явлениях Решение однородных тригонометрических уравнений
Решение однородных тригонометрических уравнений Презентация на тему ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
Презентация на тему ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ  Определение длины остряков и тяговых усилий для их перевода
Определение длины остряков и тяговых усилий для их перевода Презентация на тему ГИА 2013 Модуль «Геометрия» № 9
Презентация на тему ГИА 2013 Модуль «Геометрия» № 9