Содержание
- 2. Круговым конусом называется тело ограниченное кругом – основанием конуса, и конической поверхностью, образованной отрезками, соединяющими точку,
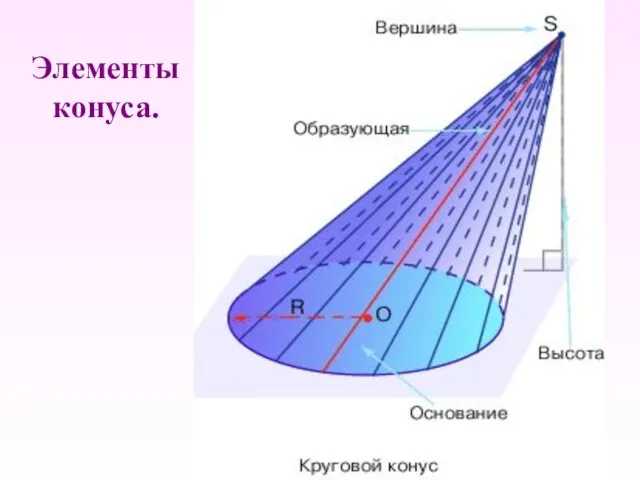
- 3. Элементы конуса.
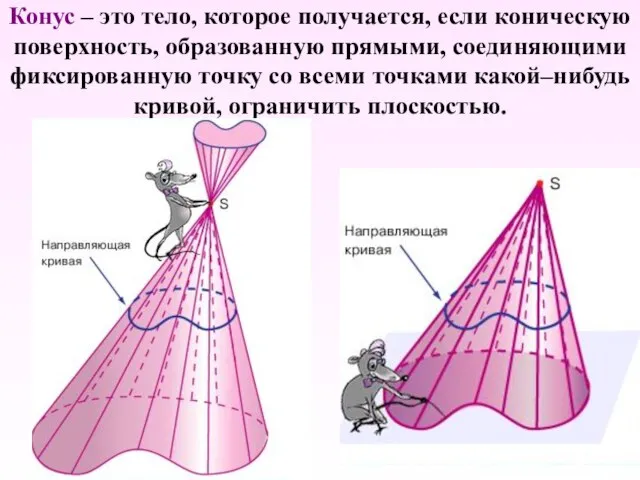
- 4. Конус – это тело, которое получается, если коническую поверхность, образованную прямыми, соединяющими фиксированную точку со всеми
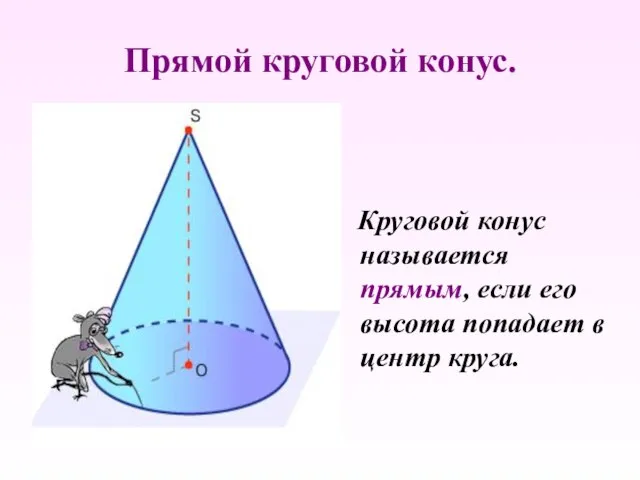
- 5. Прямой круговой конус. Круговой конус называется прямым, если его высота попадает в центр круга.
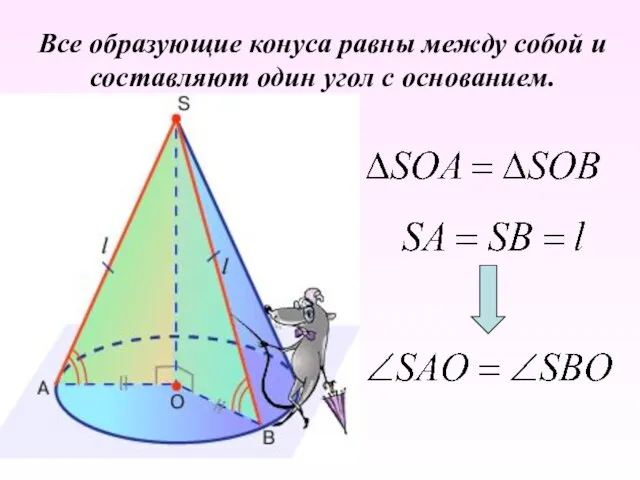
- 6. Все образующие конуса равны между собой и составляют один угол с основанием.
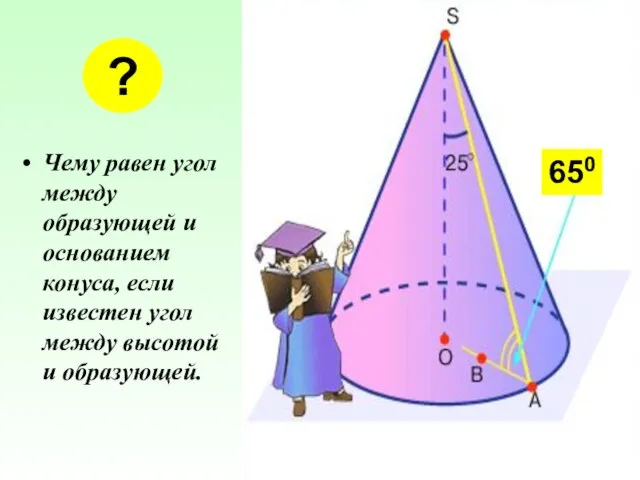
- 7. Чему равен угол между образующей и основанием конуса, если известен угол между высотой и образующей. ?
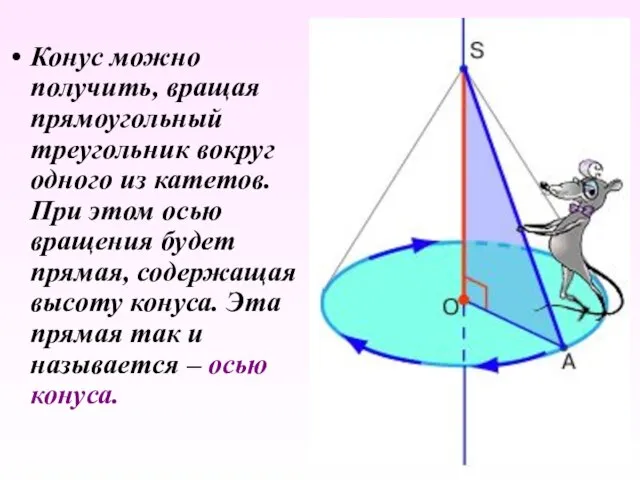
- 8. Конус можно получить, вращая прямоугольный треугольник вокруг одного из катетов. При этом осью вращения будет прямая,
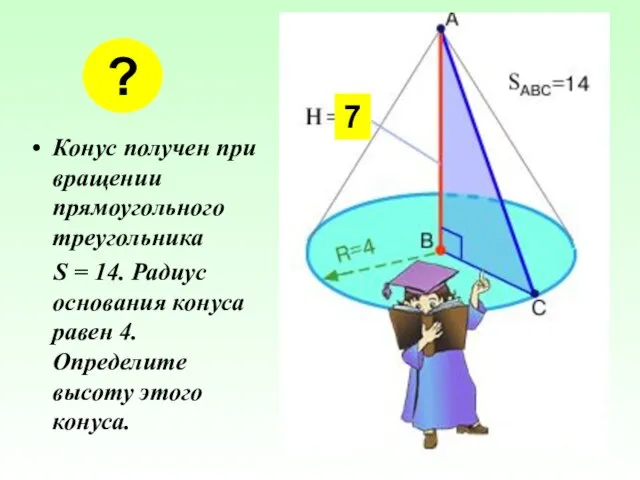
- 9. Конус получен при вращении прямоугольного треугольника S = 14. Радиус основания конуса равен 4. Определите высоту
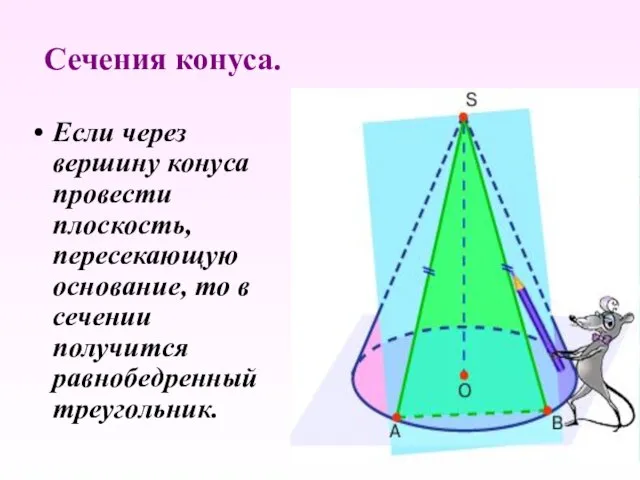
- 10. Сечения конуса. Если через вершину конуса провести плоскость, пересекающую основание, то в сечении получится равнобедренный треугольник.
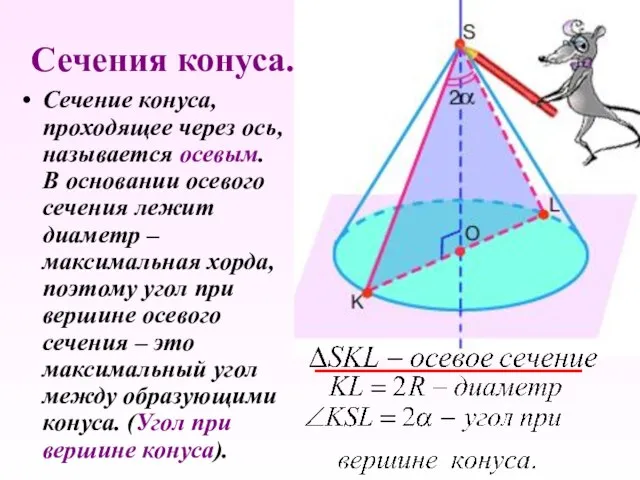
- 11. Сечение конуса, проходящее через ось, называется осевым. В основании осевого сечения лежит диаметр – максимальная хорда,
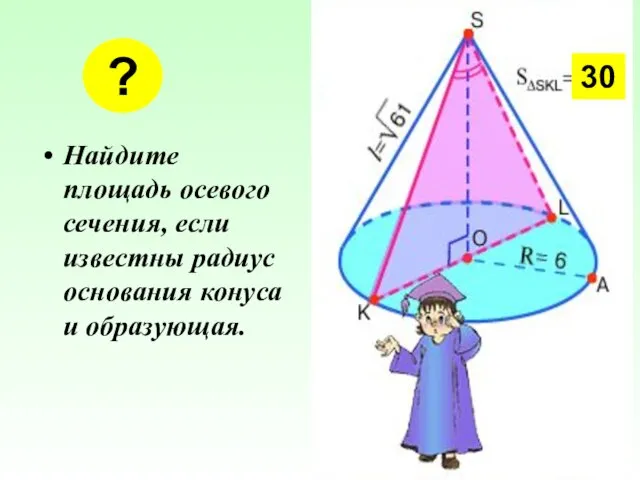
- 12. Найдите площадь осевого сечения, если известны радиус основания конуса и образующая. ? 30
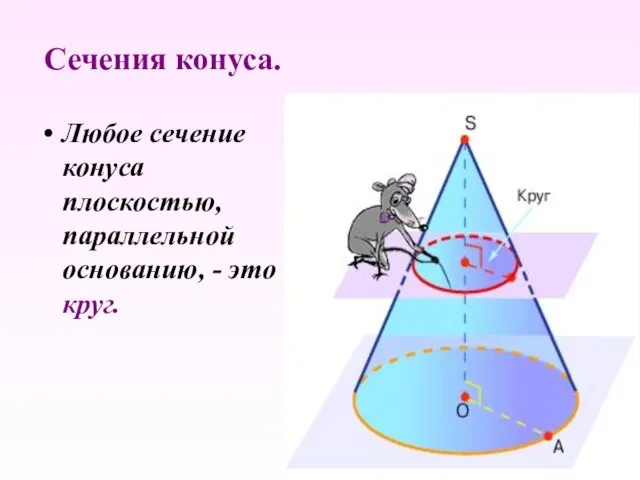
- 13. Любое сечение конуса плоскостью, параллельной основанию, - это круг. Сечения конуса.
- 14. Через середину высоты конуса провели плоскость, перпендикулярную оси, и получили круг R = 5. Чему равна
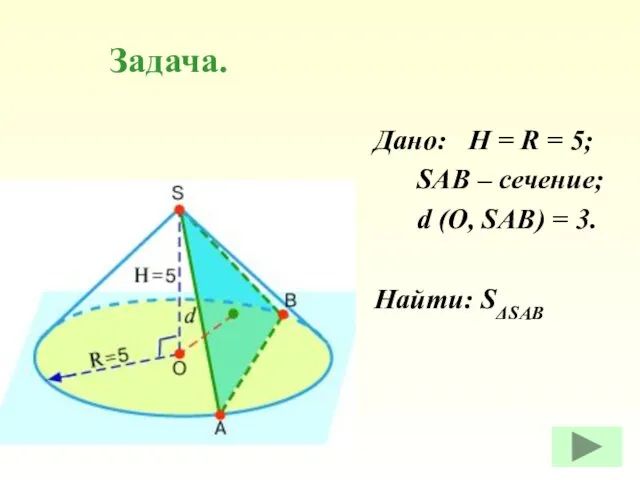
- 15. Задача. Дано: H = R = 5; SAB – сечение; d (O, SAB) = 3. Найти:
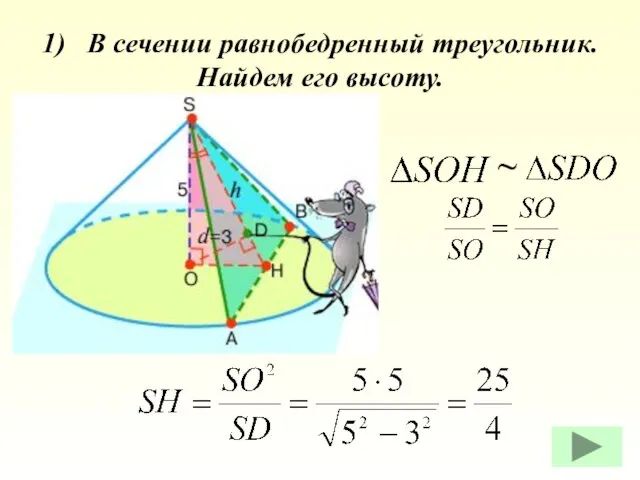
- 16. 1) В сечении равнобедренный треугольник. Найдем его высоту. ~
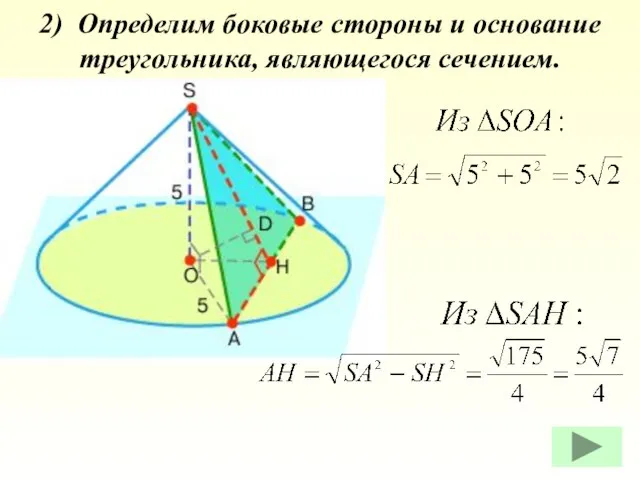
- 17. 2) Определим боковые стороны и основание треугольника, являющегося сечением.
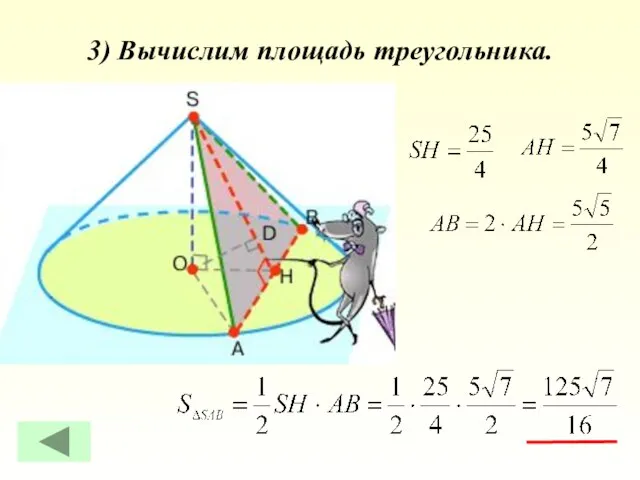
- 18. 3) Вычислим площадь треугольника.
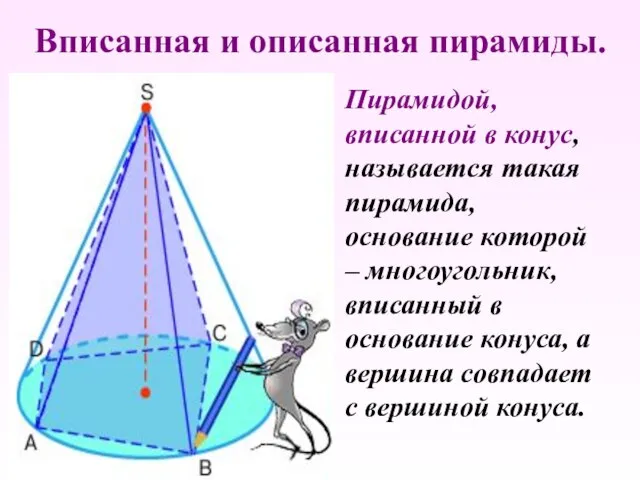
- 19. Вписанная и описанная пирамиды. Пирамидой, вписанной в конус, называется такая пирамида, основание которой – многоугольник, вписанный
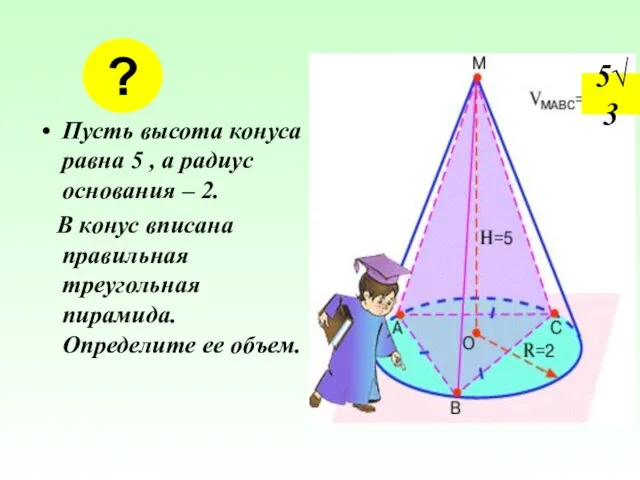
- 20. Пусть высота конуса равна 5 , а радиус основания – 2. В конус вписана правильная треугольная
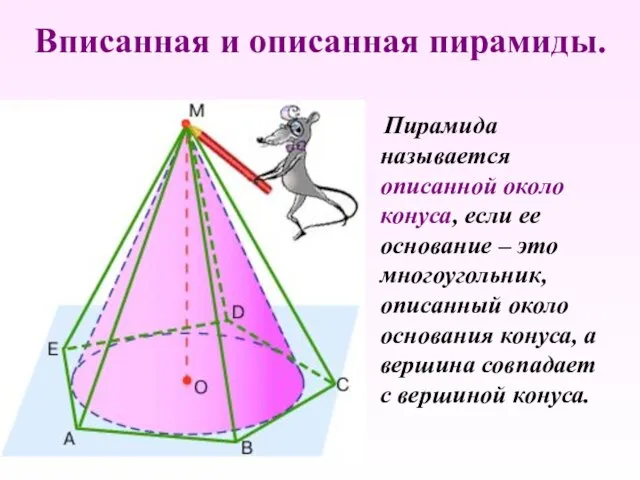
- 21. Пирамида называется описанной около конуса, если ее основание – это многоугольник, описанный около основания конуса, а
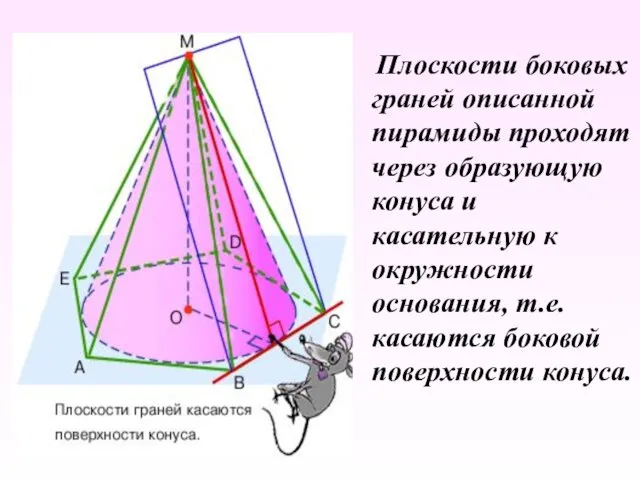
- 22. Плоскости боковых граней описанной пирамиды проходят через образующую конуса и касательную к окружности основания, т.е. касаются
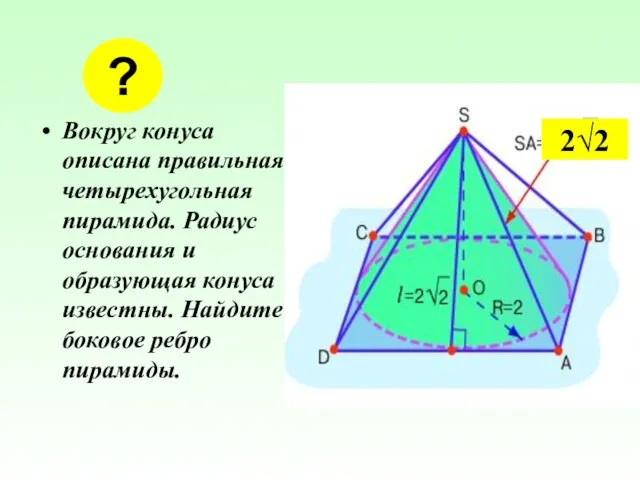
- 23. Вокруг конуса описана правильная четырехугольная пирамида. Радиус основания и образующая конуса известны. Найдите боковое ребро пирамиды.
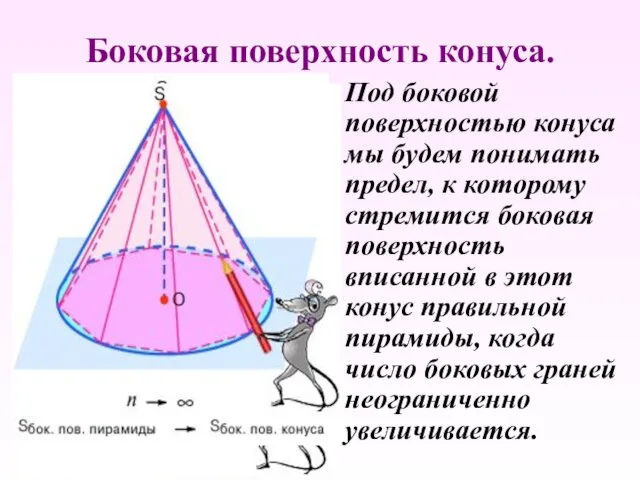
- 24. Боковая поверхность конуса. Под боковой поверхностью конуса мы будем понимать предел, к которому стремится боковая поверхность
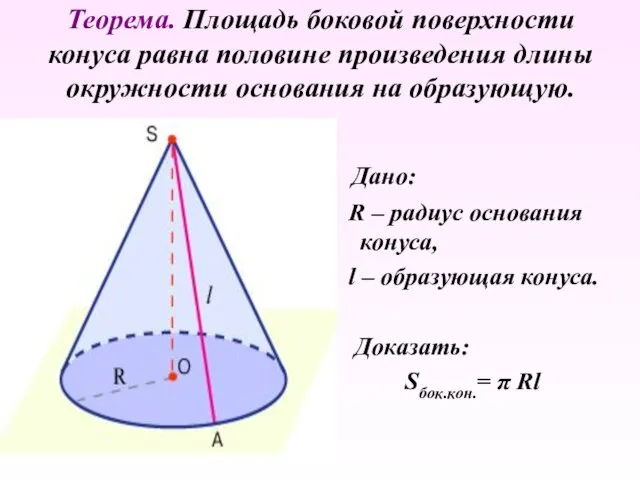
- 25. Теорема. Площадь боковой поверхности конуса равна половине произведения длины окружности основания на образующую. Дано: R –
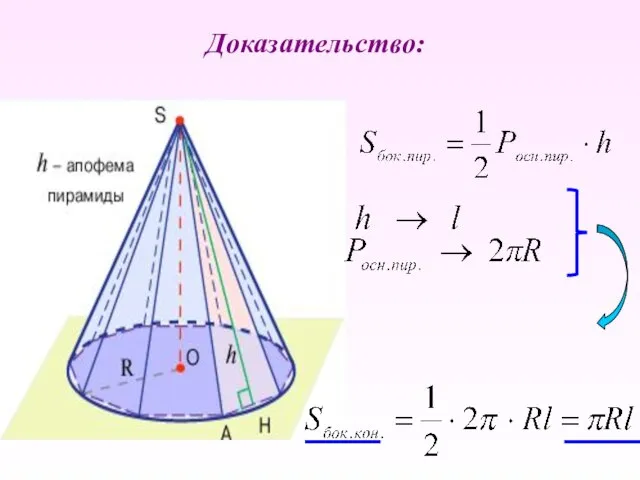
- 26. Доказательство:
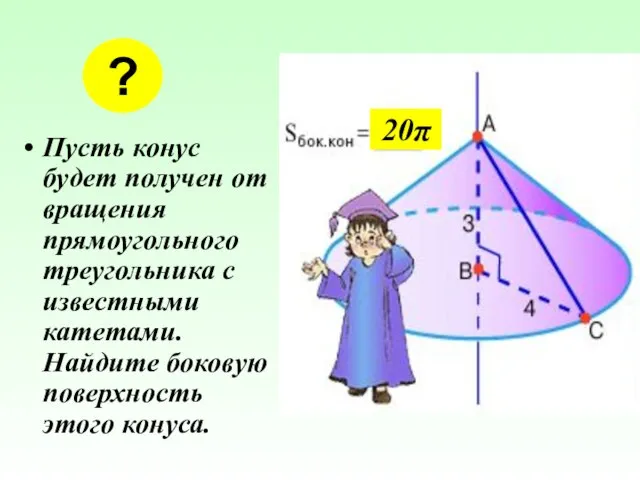
- 27. Пусть конус будет получен от вращения прямоугольного треугольника с известными катетами. Найдите боковую поверхность этого конуса.
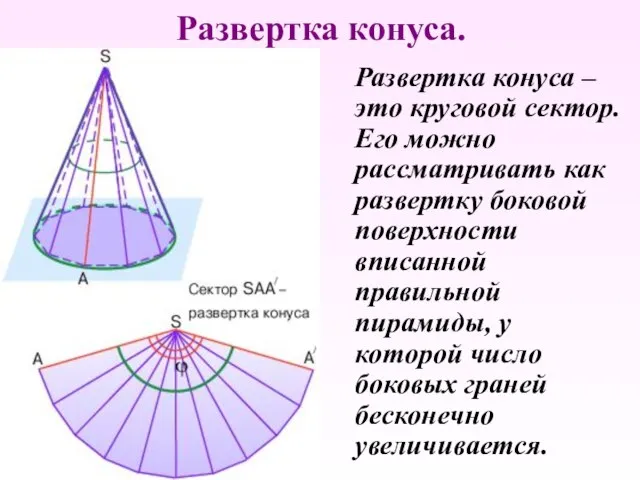
- 28. Развертка конуса. Развертка конуса – это круговой сектор. Его можно рассматривать как развертку боковой поверхности вписанной
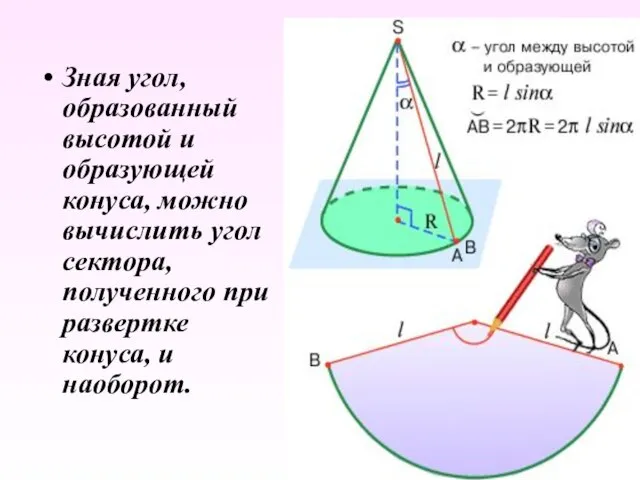
- 29. Зная угол, образованный высотой и образующей конуса, можно вычислить угол сектора, полученного при развертке конуса, и
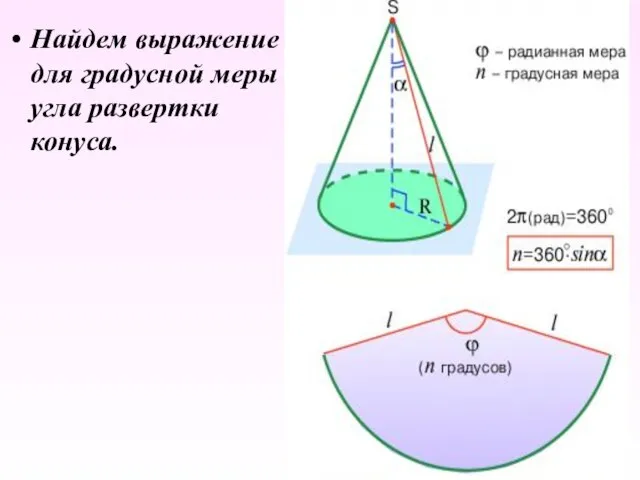
- 30. Найдем выражение для градусной меры угла развертки конуса.
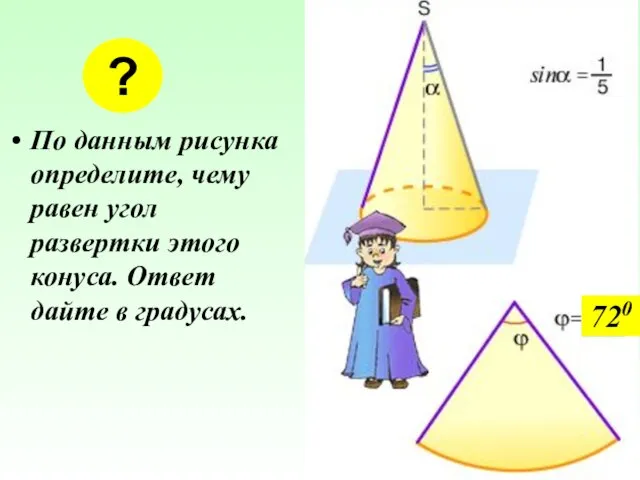
- 31. По данным рисунка определите, чему равен угол развертки этого конуса. Ответ дайте в градусах. ? 720
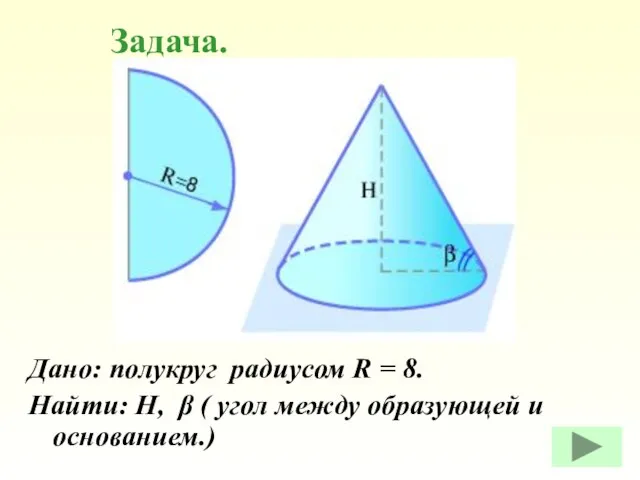
- 32. Дано: полукруг радиусом R = 8. Найти: Н, β ( угол между образующей и основанием.) Задача.
- 33. 1) Используем формулу, связывающую угол кругового сектора развертки с углом между высотой и образующей конуса. Получим
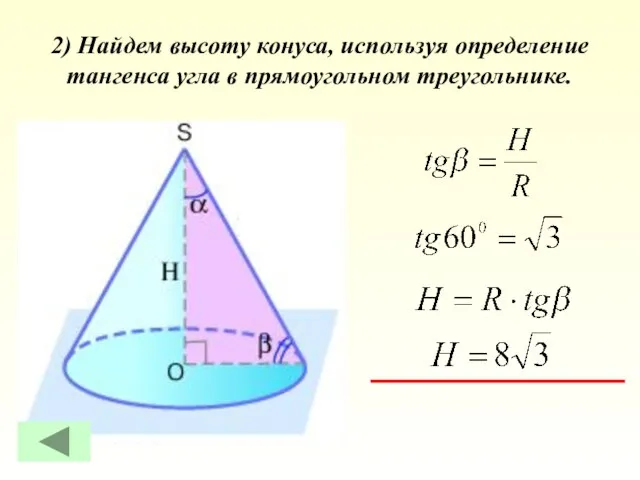
- 34. 2) Найдем высоту конуса, используя определение тангенса угла в прямоугольном треугольнике.
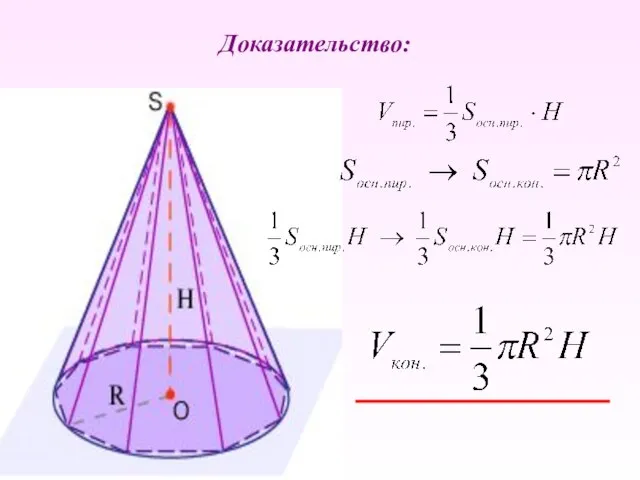
- 35. Объем конуса. Дано: R – радиус основания Н – высота конуса Доказать: Vкон.= 1/3 Sосн.H Теорема.
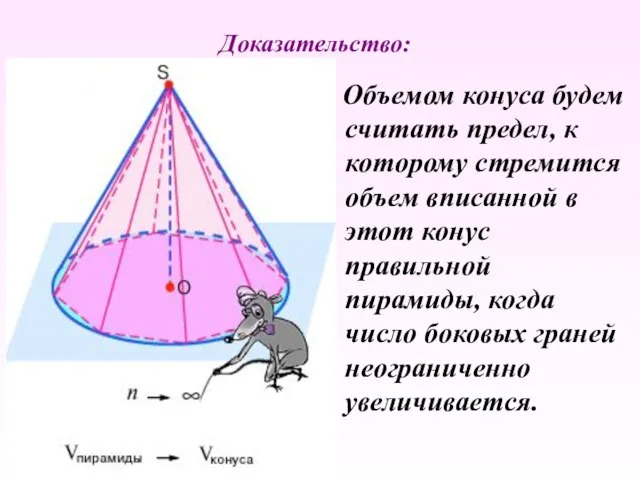
- 36. Объемом конуса будем считать предел, к которому стремится объем вписанной в этот конус правильной пирамиды, когда
- 37. Доказательство:
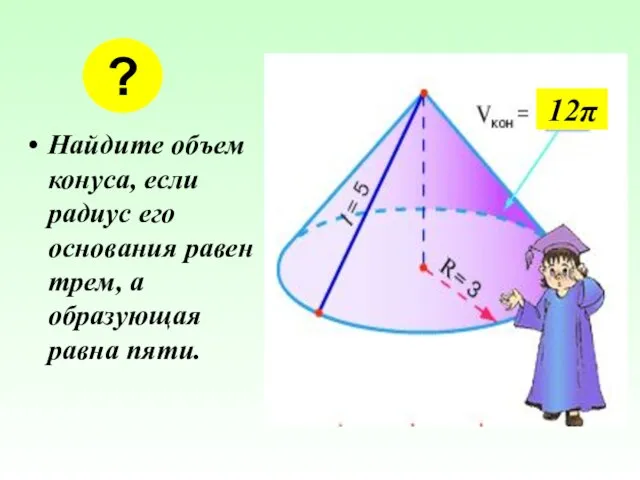
- 38. Найдите объем конуса, если радиус его основания равен трем, а образующая равна пяти. ? 12π
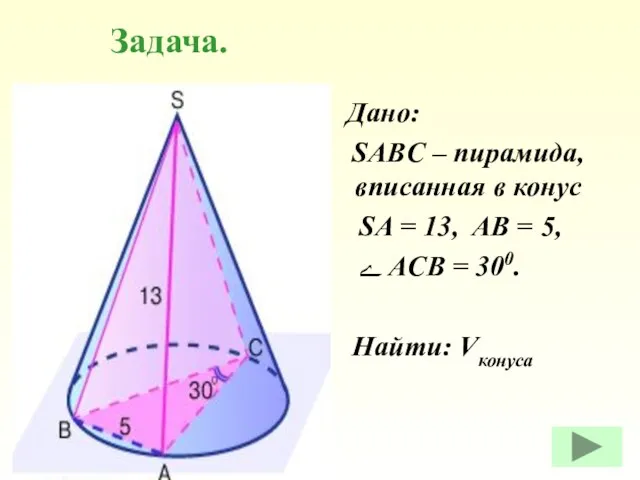
- 39. Дано: SABC – пирамида, вписанная в конус SA = 13, AB = 5, ے ACB =
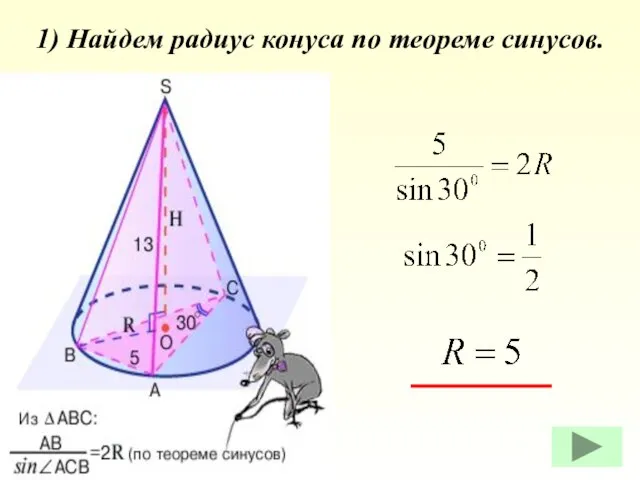
- 40. 1) Найдем радиус конуса по теореме синусов.
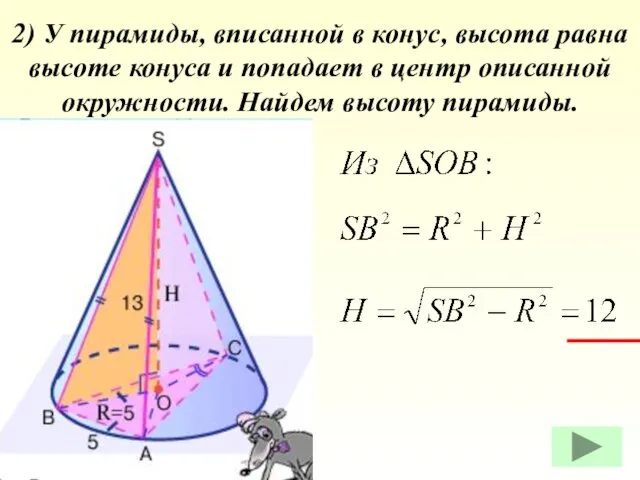
- 41. 2) У пирамиды, вписанной в конус, высота равна высоте конуса и попадает в центр описанной окружности.
- 43. Скачать презентацию




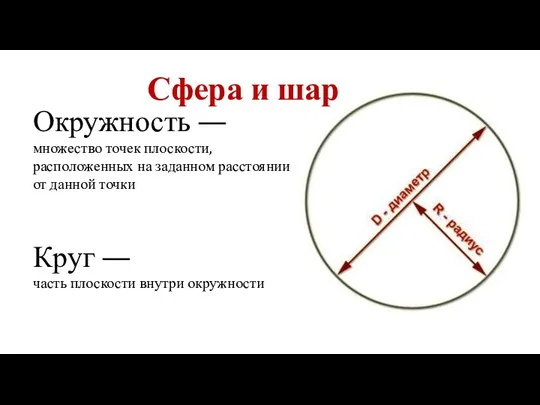 Сфера и шар
Сфера и шар Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ
Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ  Деление. Неправильные дроби
Деление. Неправильные дроби Геометрия в живописи
Геометрия в живописи Угол между прямой и плоскостью
Угол между прямой и плоскостью Задачи на прогрессию
Задачи на прогрессию Поверхностные интегралы первого рода
Поверхностные интегралы первого рода Степенная функция
Степенная функция Уравнение Бернулли
Уравнение Бернулли Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Площадь поверхности цилиндра
Площадь поверхности цилиндра Параллельные прямые
Параллельные прямые Ромб. Решение 6 задачи
Ромб. Решение 6 задачи Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики B7
B7 Презентация на тему Принцип Дирихле
Презентация на тему Принцип Дирихле  Основы теории вероятностей или случайные события ( лекция 2)
Основы теории вероятностей или случайные события ( лекция 2)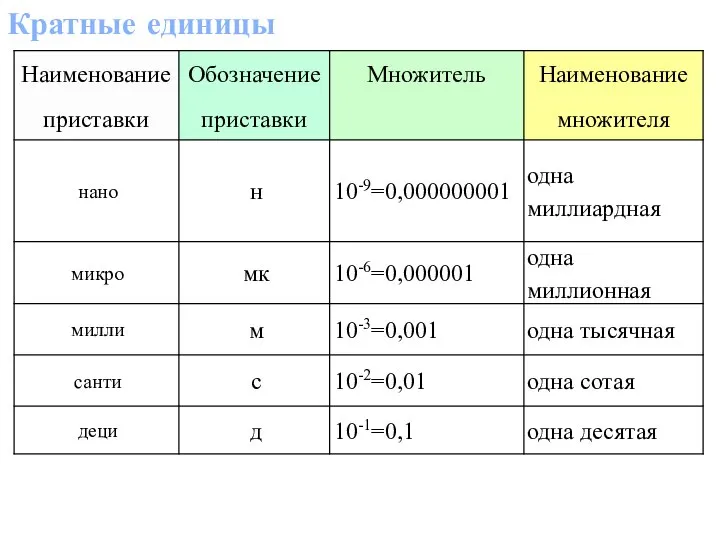 Кратные единицы
Кратные единицы Алгебра. Задачник, часть 2
Алгебра. Задачник, часть 2 Треугольники, задача
Треугольники, задача Прямоугольник
Прямоугольник Устный счёт. Для 5 коррекционного класса VIII вида
Устный счёт. Для 5 коррекционного класса VIII вида Олимпиадная математика. Доказательство от противного
Олимпиадная математика. Доказательство от противного Естественно балансирующееся общество
Естественно балансирующееся общество ریاضی جزوه کامل
ریاضی جزوه کامل Таблица Шульте
Таблица Шульте Понятие производной
Понятие производной Почти все об углах
Почти все об углах