Содержание
- 2. Параллельный перенос и Поворот.
- 3. Содержание. Основные виды движений. Определения: Движение. Поворот. Параллельный перенос.
- 4. Осевая и центральная симметрии Поворот Параллельный перенос Основные виды движений:
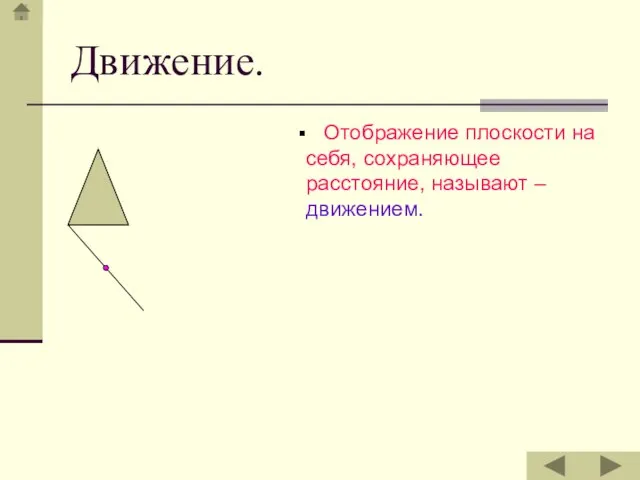
- 5. Отображение плоскости на себя, сохраняющее расстояние, называют – движением. Движение.
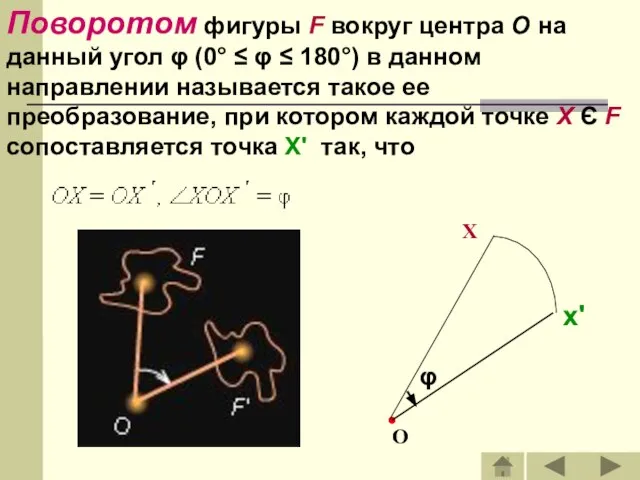
- 6. Поворотом фигуры F вокруг центра O на данный угол φ (0° ≤ φ ≤ 180°) в
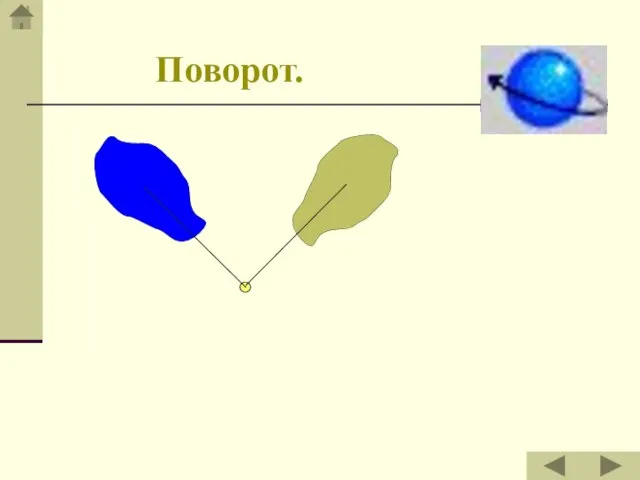
- 7. Поворот.
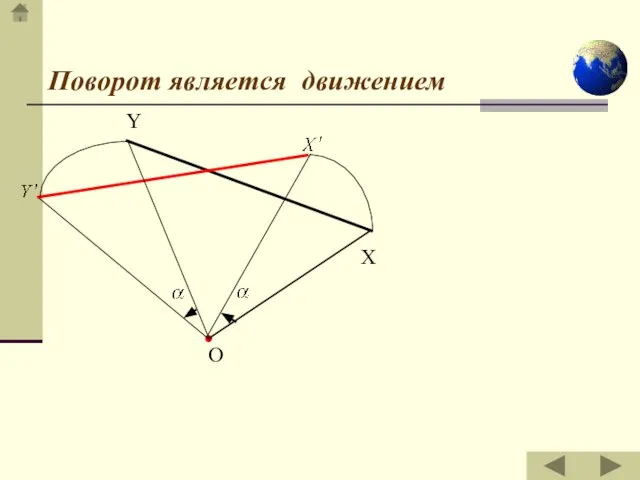
- 8. Поворот является движением О Y X
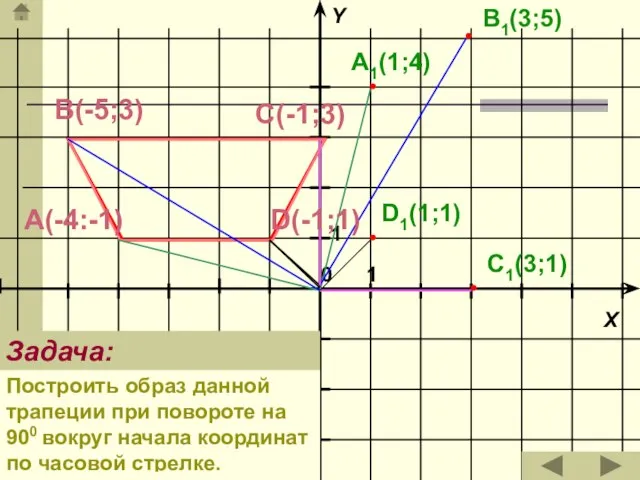
- 9. А(-4:-1) В(-5;3) D(-1;1) С(-1;3) A1(1;4) B1(3;5) C1(3;1) D1(1;1) Задача: Построить образ данной трапеции при повороте на
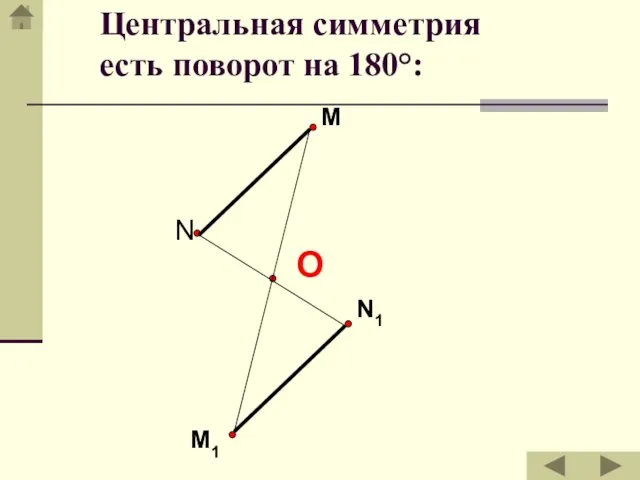
- 10. M N N1 M1 Центральная симметрия есть поворот на 180°: О
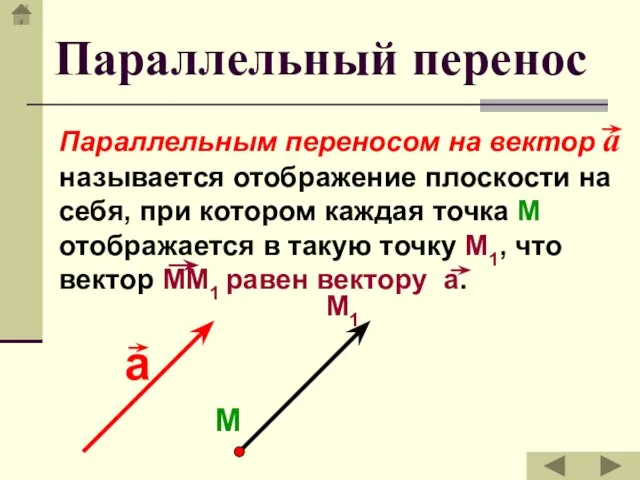
- 11. Параллельный перенос Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка
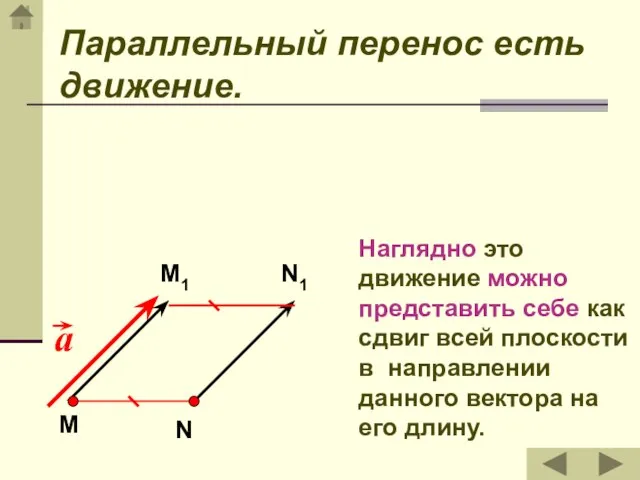
- 12. Параллельный перенос есть движение. Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении
- 13. Параллельный перенос на плоскости в системе координат. Введем на плоскости систему координат O, X, Y. Преобразование
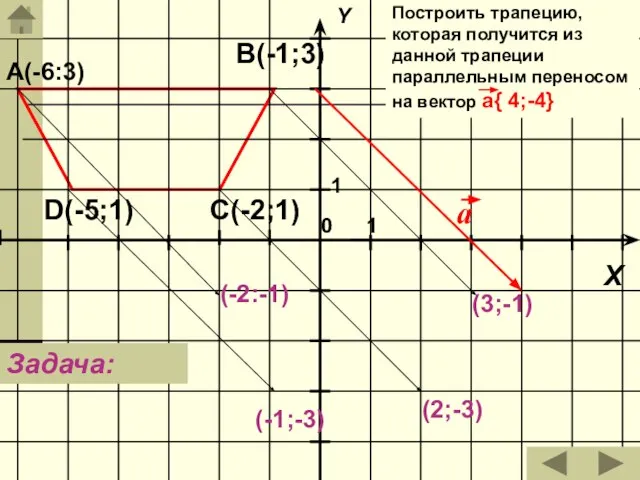
- 14. А(-6:3) В(-1;3) С(-2;1) D(-5;1) Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор a{
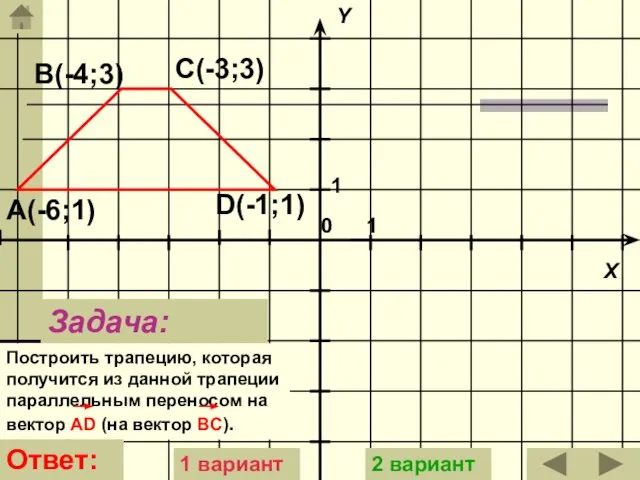
- 15. Задача: Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор АD (на вектор BC).
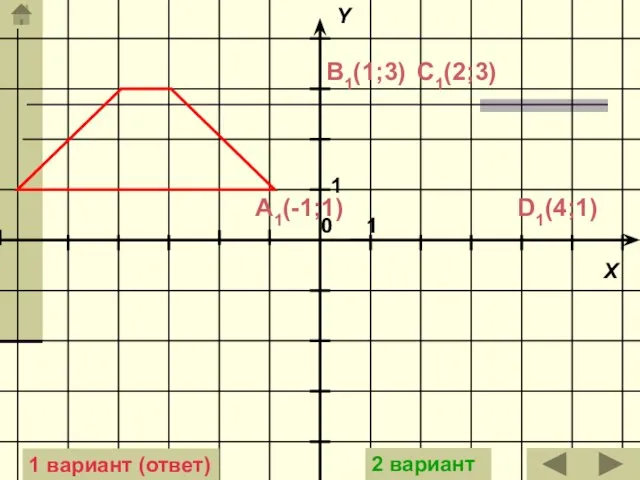
- 16. C1(2;3) D1(4;1) B1(1;3) A1(-1;1) 1 вариант (ответ) 2 вариант
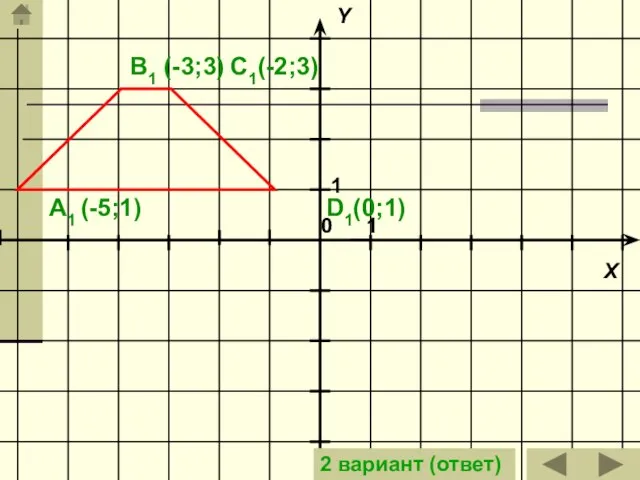
- 17. A1 (-5;1) B1 (-3;3) C1(-2;3) D1(0;1) 2 вариант (ответ)
- 19. Скачать презентацию




 Деление на 3
Деление на 3 Дифференциальные уравнения 1-го порядка
Дифференциальные уравнения 1-го порядка Факторный анализ торговых алгоритмов
Факторный анализ торговых алгоритмов Математическое моделирование. Лекция 1
Математическое моделирование. Лекция 1 Төзек күпкырлыклар
Төзек күпкырлыклар Признаки параллельности прямых
Признаки параллельности прямых Тригонометрические уравнения. Устный счет
Тригонометрические уравнения. Устный счет Повторение и расширение сведений о функции
Повторение и расширение сведений о функции Отношение площадей подобных треугольников
Отношение площадей подобных треугольников Хитрые задачи. 4 класс
Хитрые задачи. 4 класс Состав числа 10
Состав числа 10 Метод параллельного переноса решения геометрических задач
Метод параллельного переноса решения геометрических задач Уравнения и неравенства в целых числах
Уравнения и неравенства в целых числах Задачи. Урок 20
Задачи. Урок 20 Квадратные уравнения и неравенства
Квадратные уравнения и неравенства Показательные уравнения
Показательные уравнения Решение иррациональных уравнений
Решение иррациональных уравнений Співвідношення між тригонометричними функціями
Співвідношення між тригонометричними функціями Презентация по математике "Решение задач с помощью систем уравнений второй степени" -
Презентация по математике "Решение задач с помощью систем уравнений второй степени" -  Преобразование иррациональных выражений
Преобразование иррациональных выражений КВН Знакомьтесь: геометрия
КВН Знакомьтесь: геометрия Формулы дифференцирования
Формулы дифференцирования Математика. 2 класс
Математика. 2 класс Задача о смесях
Задача о смесях Признаки и свойства параллельных прямых
Признаки и свойства параллельных прямых Цилиндр. Ось симметрии цилиндра
Цилиндр. Ось симметрии цилиндра Построение треугольника
Построение треугольника Руководитель кружка по математике для 7 класса
Руководитель кружка по математике для 7 класса