Содержание
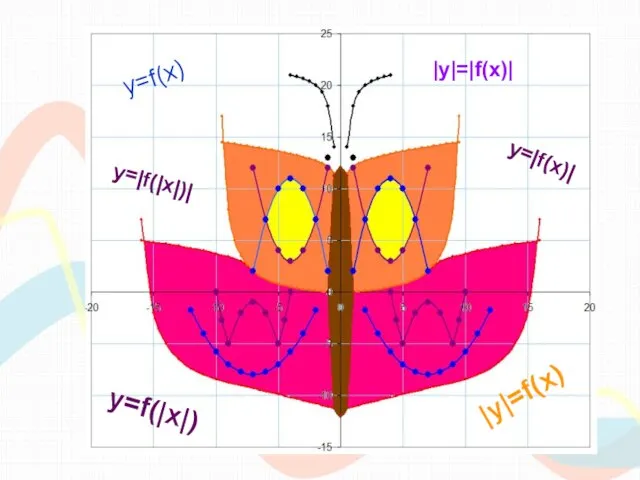
- 2. y=f(x) y=|f(x)| y=f(|x|) |y|=f(x) |y|=|f(x)| y=|f(|x|)|
- 3. Актуальность: Эта тема актуальна, т.к. в конце 11 класса необходимо сдавать единый государственный экзамен по математике,
- 4. Цель: Изучение способов построения графиков функций с помощью различных преобразований. Задачи: Исследовать взаимосвязь графика функции y=f(x)
- 5. Рабочая гипотеза: графики сложных функций, можно построить с помощью преобразований графика исходной функции. Объект – графики
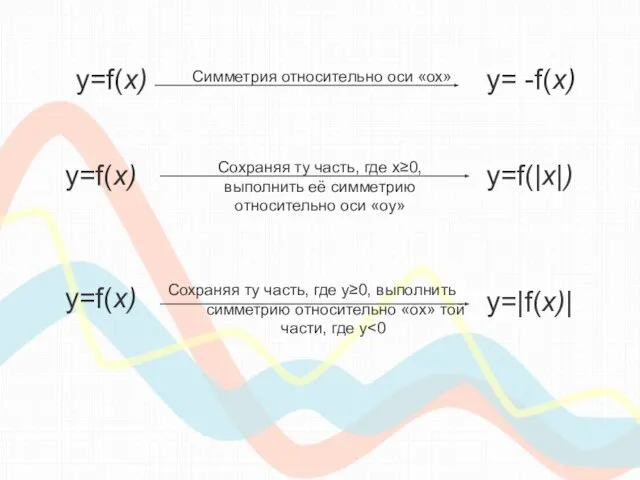
- 6. y=f(х) y= -f(х) Симметрия относительно оси «ох» y=f(х) y=f(|х|) Сохраняя ту часть, где х≥0, выполнить её
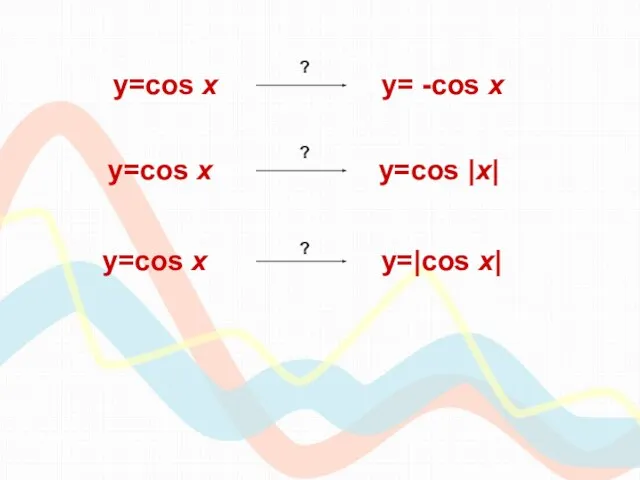
- 7. y=cos х y=cos |x| y=cos х y= -cos x y=cos х y=|cos x| ? ? ?
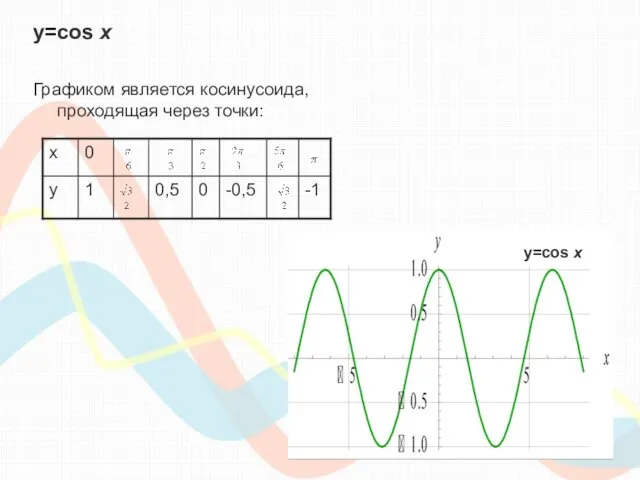
- 8. y=cos х Графиком является косинусоида, проходящая через точки: y=cos х
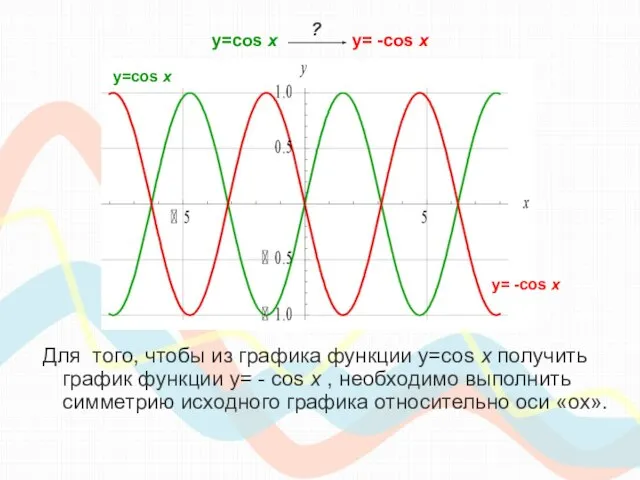
- 9. y=cos х y= -cos x Для того, чтобы из графика функции y=cos x получить график функции
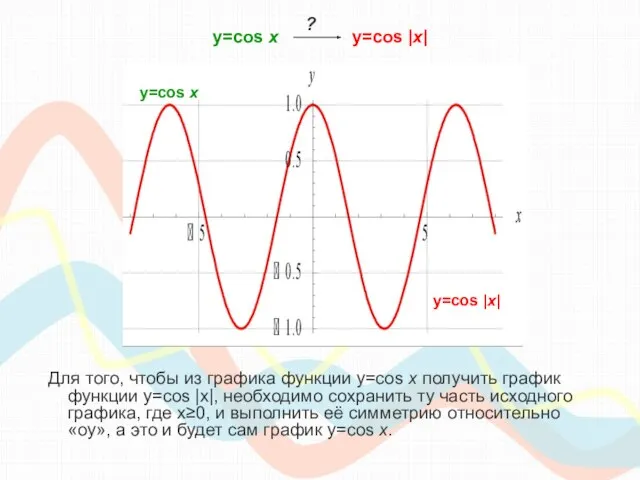
- 10. y=cos х y=cos |x| Для того, чтобы из графика функции y=cos x получить график функции y=cos
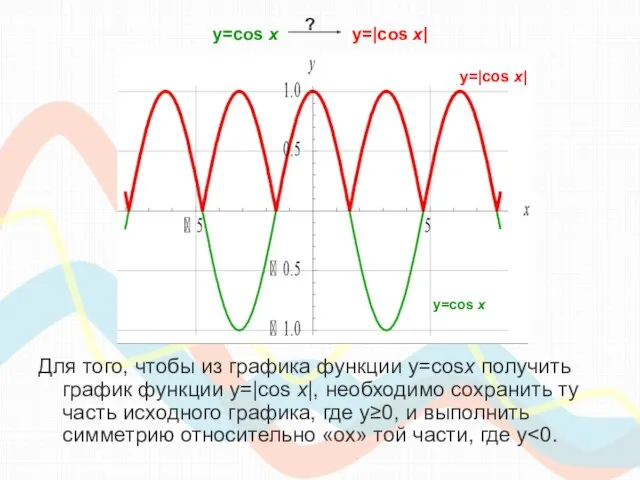
- 11. y=cos х y=|cos x| Для того, чтобы из графика функции y=cosx получить график функции y=|cos x|,
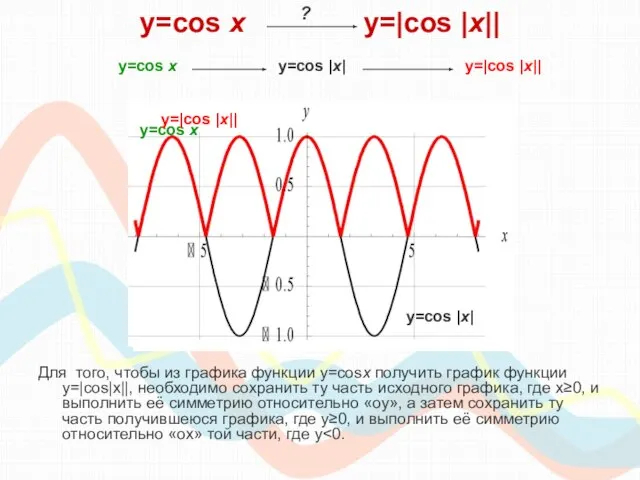
- 12. y=cos х y=|cos |x|| Для того, чтобы из графика функции y=cosx получить график функции y=|cos|x||, необходимо
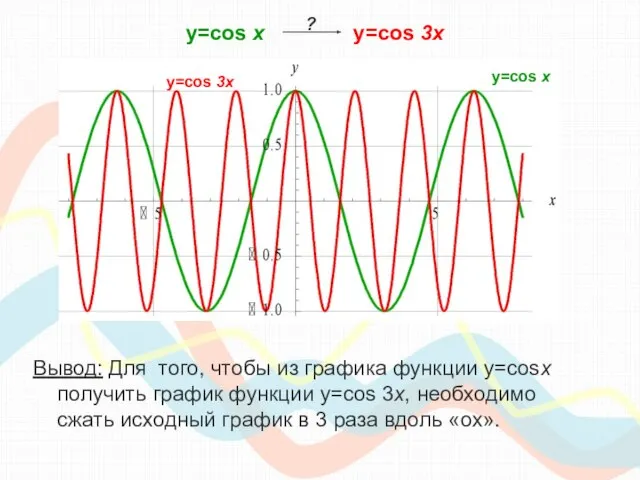
- 13. y=cos х y=cos 3x y=cos 3x График этой функции проходит через точки: ?
- 14. y=cos х y=cos 3x Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos
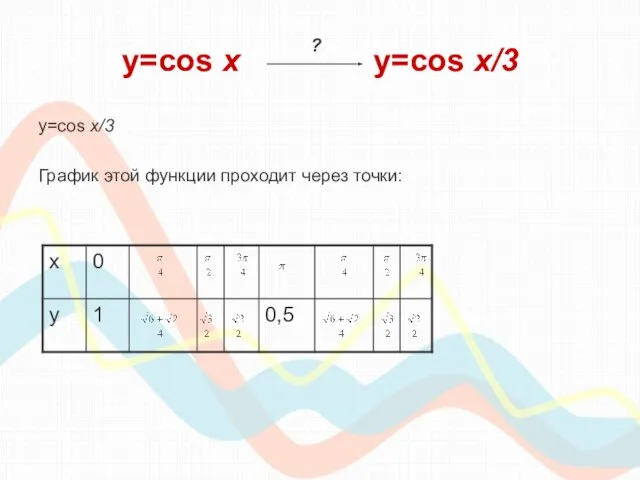
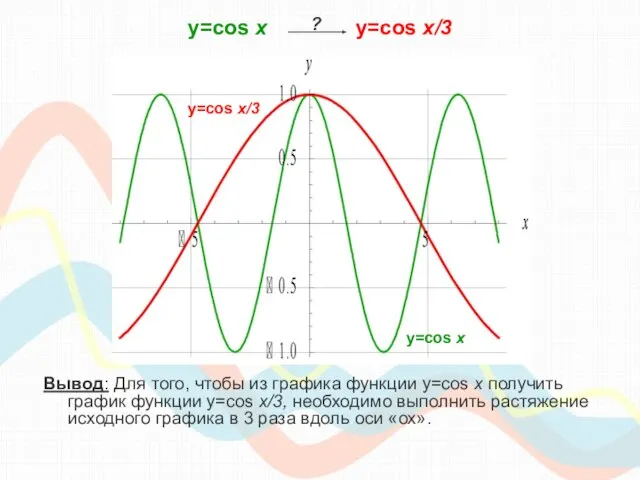
- 15. y=cos х y=cos x/3 y=cos x/3 График этой функции проходит через точки: ?
- 16. y=cos х y=cos x/3 Вывод: Для того, чтобы из графика функции y=cos x получить график функции
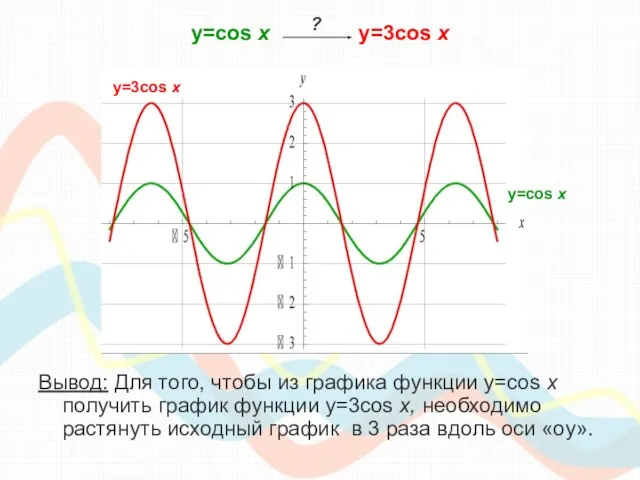
- 17. y=cos х y=3cos x y=3cos x График проходит через точки: ?
- 18. y=cos х y=3cos x Вывод: Для того, чтобы из графика функции y=cos x получить график функции
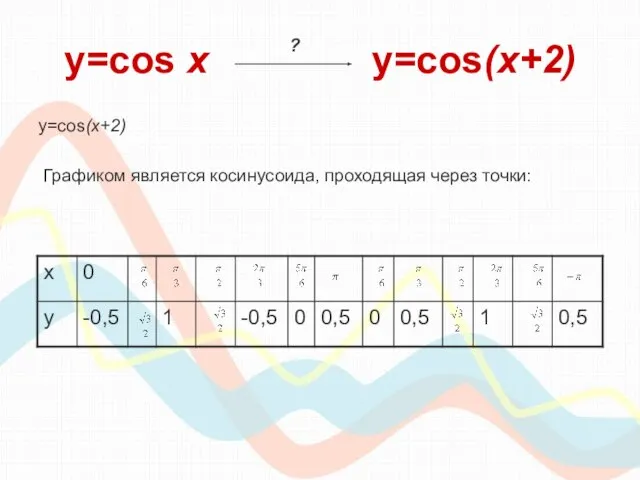
- 19. y=cos х y=cos(x+2) y=cos(x+2) Графиком является косинусоида, проходящая через точки: ?
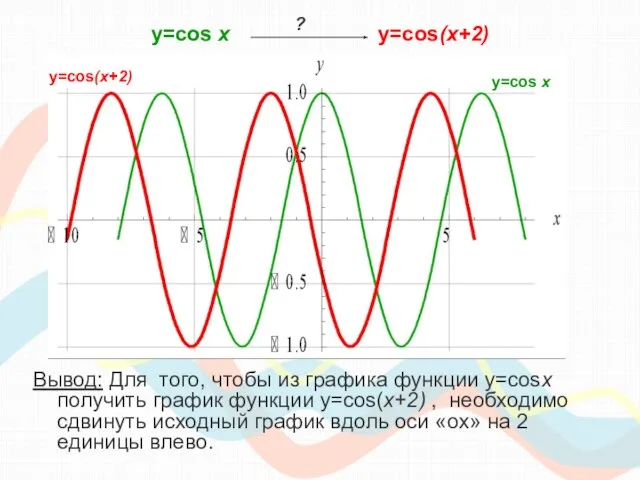
- 20. y=cos х y=cos(x+2) Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos(x+2) ,
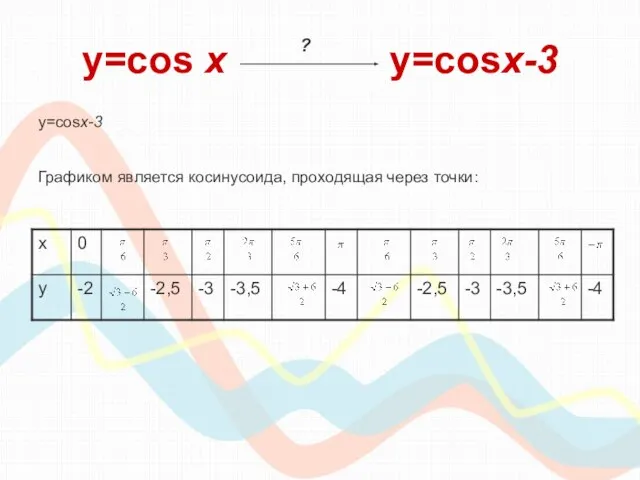
- 21. y=cos х y=cosx-3 y=cosx-3 Графиком является косинусоида, проходящая через точки: ?
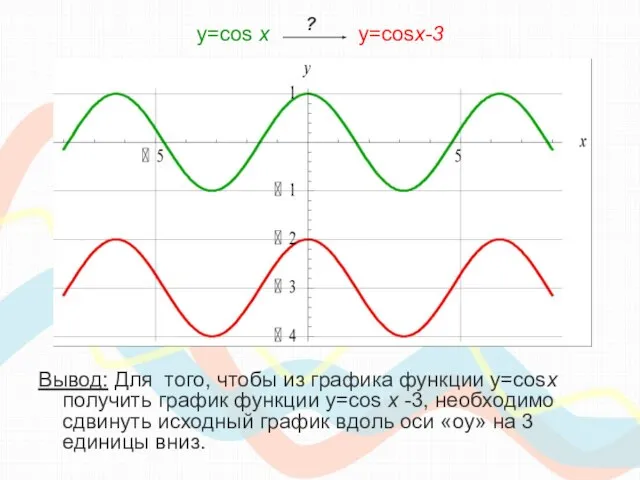
- 22. y=cos х y=cosx-3 Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos x
- 23. Итог: y=f(x) y=f(|x|) Сохраняя ту часть исходного графика, где х≥0, выполнить её симметрию относительно оси «оу»
- 24. Мы знаем, что для того, чтобы из графика функции получить график функции необходимо растянуть исходный график
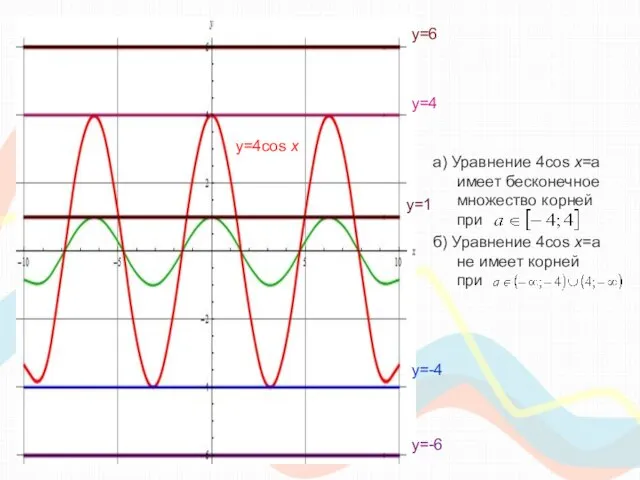
- 25. а) Уравнение 4cos x=a имеет бесконечное множество корней при б) Уравнение 4cos x=a не имеет корней
- 26. Исследование количества корней уравнения: |cos 2x|=x² y=|cos 2x| y=cos x y=cos 2x y=|cos 2x| Мы знаем,
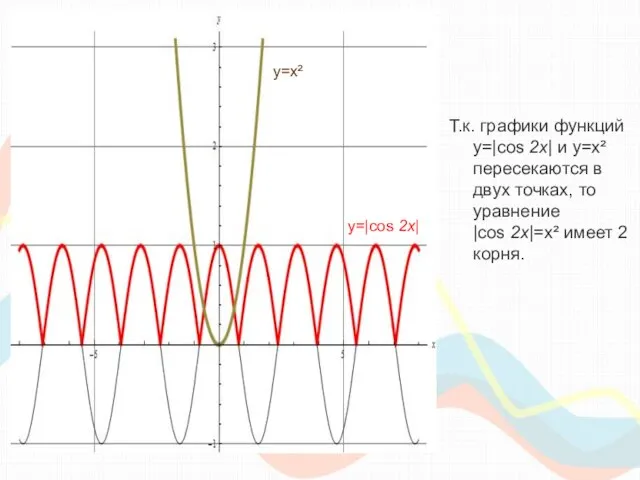
- 27. Т.к. графики функций y=|cos 2x| и y=x² пересекаются в двух точках, то уравнение |cos 2x|=x² имеет
- 28. Функции, использованные для построения рисунка
- 33. Заключение Цель достигнута, мы изучили способы построения графиков функций с помощью различных преобразований. Задачи выполнены, мы
- 34. Значимость полученных результатов: сейчас нам стало известно, как строить графики сложных функций с помощью преобразований графика
- 36. Скачать презентацию












 Собирательные числительные
Собирательные числительные Нахождение дроби от числа
Нахождение дроби от числа Логические и традиционные головоломки
Логические и традиционные головоломки Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля
Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля ОГЭ. Приемы решения практикоориентированных задач
ОГЭ. Приемы решения практикоориентированных задач Деление трехзначного числа на двухзначное число
Деление трехзначного числа на двухзначное число Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Математика в профессии сварщика
Математика в профессии сварщика Презентация на тему СВОЙСТВА ДВИЖЕНИЯ
Презентация на тему СВОЙСТВА ДВИЖЕНИЯ  Векторы. Действия с векторами
Векторы. Действия с векторами Презентация на тему Обыкновенные дроби
Презентация на тему Обыкновенные дроби  Комбинаторика
Комбинаторика Статистика, часть 6. Условные обозначения
Статистика, часть 6. Условные обозначения математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Найпростіші тригонометричні рівняння
Найпростіші тригонометричні рівняння Числовые последовательности. Арифметическая прогрессия
Числовые последовательности. Арифметическая прогрессия Задача о нахождении стороны квадрата
Задача о нахождении стороны квадрата Урок математики во 2 классе. Повторение
Урок математики во 2 классе. Повторение Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)
Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)  Функция. Область определения и область значений функции
Функция. Область определения и область значений функции Построение композиции из геометрических тел
Построение композиции из геометрических тел Множество. Элемент множества
Множество. Элемент множества Интерактивные тренинги по геометрии для подготовки к ОГЭ
Интерактивные тренинги по геометрии для подготовки к ОГЭ Разложение многочлена на множители
Разложение многочлена на множители Трапеция. Площадь криволинейной трапеции
Трапеция. Площадь криволинейной трапеции Провешивание прямой на местности
Провешивание прямой на местности Презентация на тему Решение неравенств методом интервалов (9 класс)
Презентация на тему Решение неравенств методом интервалов (9 класс)  Взаимное расположение прямой и окружности. 8 класс
Взаимное расположение прямой и окружности. 8 класс