Содержание
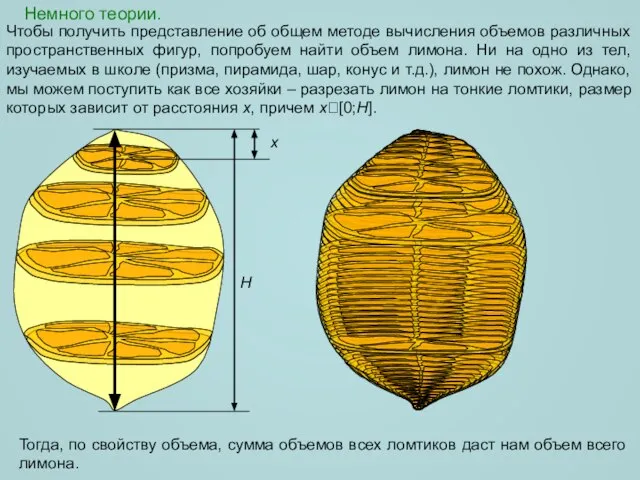
- 2. Немного теории. Чтобы получить представление об общем методе вычисления объемов различных пространственных фигур, попробуем найти объем
- 3. Немного теории. H x x С точки зрения геометрии мы построили сечения пространственной фигуры плоскостями, перпендикулярными
- 4. Немного теории (базовые классы могут пропустить). H x x Если принять число разбиений бесконечно большим числом
- 5. I. Объем прямоугольного параллелепипеда с высотой H и площадью основания S. x H x[0;H] 0 Площадь
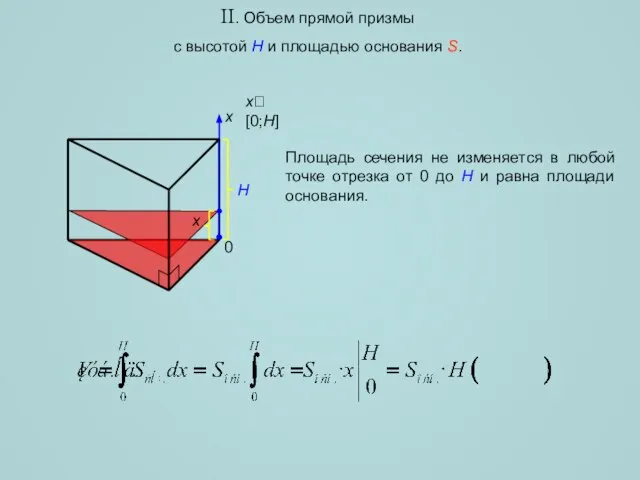
- 6. II. Объем прямой призмы с высотой H и площадью основания S. x x[0;H] H 0 Площадь
- 7. III. Объем n-угольной прямой призмы с высотой H и площадью основания S. x x[0;H] H 0
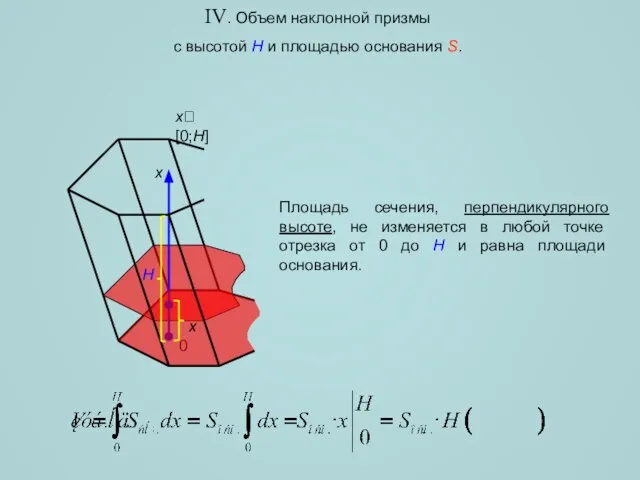
- 8. IV. Объем наклонной призмы с высотой H и площадью основания S. Площадь сечения, перпендикулярного высоте, не
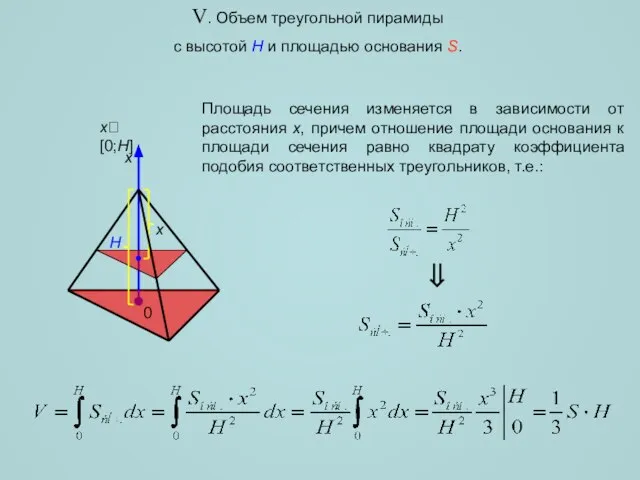
- 9. V. Объем треугольной пирамиды с высотой H и площадью основания S. H x x[0;H] ⇒ x
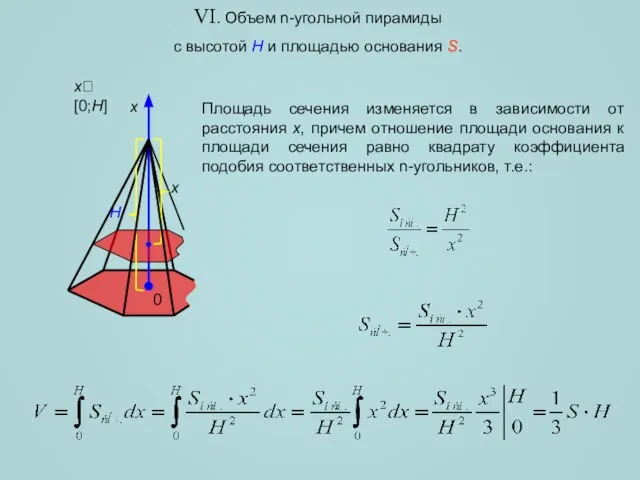
- 10. VI. Объем n-угольной пирамиды с высотой H и площадью основания S. H x Площадь сечения изменяется
- 11. VII. Объем усеченной пирамиды. текст
- 12. VIII. Объем цилиндра с высотой H и площадью основания S. x x[0;H] H 0 x Площадь
- 13. IX. Объем конуса с высотой H и площадью основания S. x x[0;H] H x Площадь сечения
- 14. X. Объем усеченного конуса. текст
- 15. XI. Объем шара с радиусом R. Найдем объем полушария, как бесконечную интегральную сумму площадей сечения с
- 16. XII. Объем шарового сегмента. Вывод объема шарового сегмента с высотой h и радиусом основания r отличается
- 17. XIII. Объем шарового слоя. текст
- 19. Скачать презентацию





![VIII. Объем цилиндра с высотой H и площадью основания S. x x[0;H]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/285360/slide-11.jpg)
![IX. Объем конуса с высотой H и площадью основания S. x x[0;H]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/285360/slide-12.jpg)


 Решение задач с использованием теоремы о накрест лежащих углах
Решение задач с использованием теоремы о накрест лежащих углах Понятие квадратного уравнения
Понятие квадратного уравнения Предел функции в точке и на бесконечности
Предел функции в точке и на бесконечности Множення і ділення звичайних дробів
Множення і ділення звичайних дробів Десятичные дроби. Колесо истории
Десятичные дроби. Колесо истории Основные понятия теории вероятностей
Основные понятия теории вероятностей Геометрические фигуры
Геометрические фигуры Обобщение по 3-м формулам сокращенного умножения
Обобщение по 3-м формулам сокращенного умножения Основные операции с логическими элементами
Основные операции с логическими элементами Габриэль Крамер
Габриэль Крамер Презентация на тему Сложение чисел с разными знаками
Презентация на тему Сложение чисел с разными знаками  Показательные неравенства
Показательные неравенства Треугольники, четырехугольники, многоугольники и их элементы. Тест
Треугольники, четырехугольники, многоугольники и их элементы. Тест Параллельность в пространстве
Параллельность в пространстве Сложение и вычитание десятичных дробей. Урок – смотр знаний. 5 класс
Сложение и вычитание десятичных дробей. Урок – смотр знаний. 5 класс Презентация на тему Свойства числовых неравенств
Презентация на тему Свойства числовых неравенств  Разложение многочленов на множители. Тест
Разложение многочленов на множители. Тест Линейная алгебра. (Матрицы, определители)
Линейная алгебра. (Матрицы, определители) Перпендикулярные прямые. Смежные и вертикальные углы
Перпендикулярные прямые. Смежные и вертикальные углы Математика. Исправляем ошибки
Математика. Исправляем ошибки Статистика
Статистика Riešenie rovníc, ak je neznáma na oboch stranách rovnice
Riešenie rovníc, ak je neznáma na oboch stranách rovnice Треугольники. Практика. Первый уровень
Треугольники. Практика. Первый уровень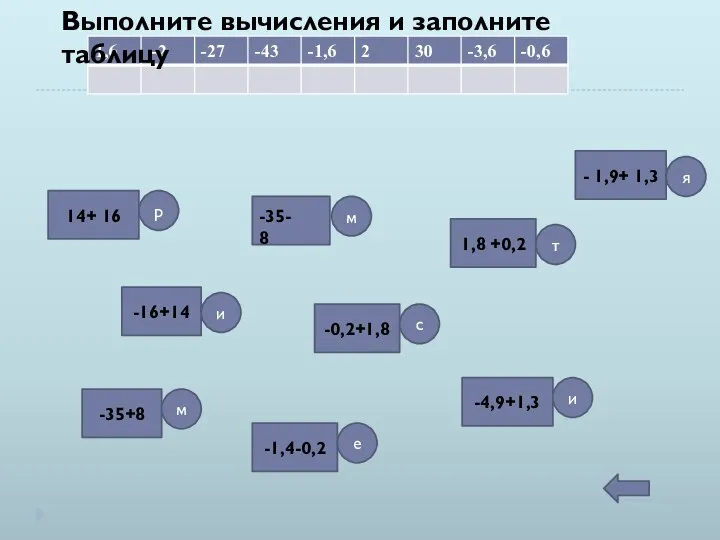 Выполните вычисления и заполните таблицу. 6 класс
Выполните вычисления и заполните таблицу. 6 класс Разнообразный мир линий
Разнообразный мир линий Математика для анализа больших данных
Математика для анализа больших данных Графики элементарных функций
Графики элементарных функций Площадь треугольника
Площадь треугольника