Задачи укладки графов. Тема 6

Планарность графов
Один и тот же граф возможно изобразить различными способами (с точностью до изоморфизма). При этом большое значение уделяется вопросам планарности.
Примеры: 1) при изготовлении электронных микросхем необходимо выяснить, можно ли схему устройства изобразить на плоскости без пересечений проводников; 2) при проектировании транспортных путей возможно избежать нежелательных перекрестков и т.д.

G1 – планарный граф,
G2 – его плоская укладка
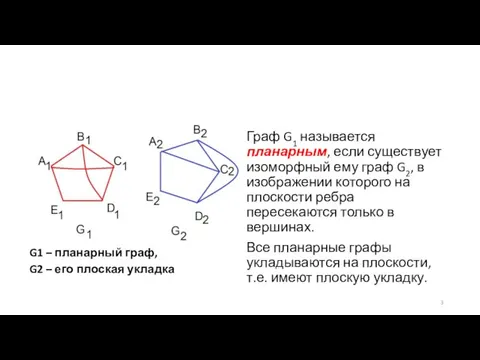
Граф G1 называется планарным, если существует изоморфный ему граф G2, в изображении которого на плоскости ребра пересекаются только в вершинах.
Все планарные графы укладываются на плоскости, т.е. имеют плоскую укладку.

Теорема 1. Любая часть (подграф) планарного графа есть планарный граф.
Теорема 2. Граф планарен тогда и только тогда, когда каждая связная компонента этого графа – планарный граф

Гранью планарного графа называется множество точек плоскости, каждая пара которых может быть соединена плоской кривой, не пересекающей ребер этого графа.
Границей грани называется множество вершин и ребер, принадлежащих этой грани

Граф G имеет три грани: Г1, Г2, Г3
Неограниченная грань Г1 – внешняя
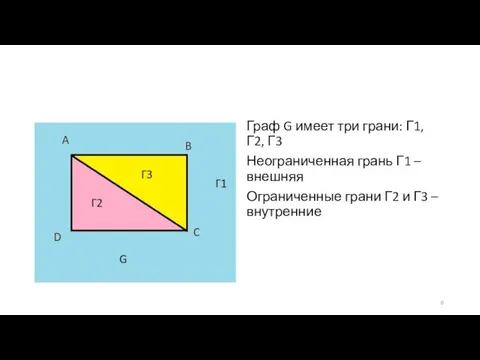
Ограниченные грани Г2 и Г3 – внутренние

Пусть n, m, f - число вершин, ребер и граней планарного графа соответственно
Теорема Эйлера
Для всякого связного планарного графа верно равенство:
n – m + f =2

Рассмотрим операцию подразбиения ребра в графе.
Операция подразбиения ребра , образованного парой вершин A и B, состоит в удалении ребра e и добавлении двух новых ребер e1 и e2, отвечающих парам вершин A, D и B, D соответственно.
Здесь D - новая (дополнительная) вершина графа.
G1 - граф до операции подразбиения ребра e, G2 – граф, получившийся в результате этой операции.
Два графа называются гомеоморфными, если они могут быть получены из одного и того же графа подразбиением его ребер.

G1 – исходный граф
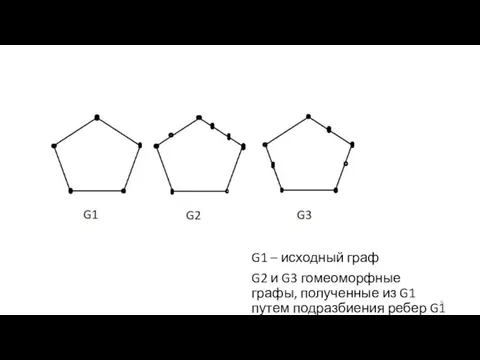
G2 и G3 гомеоморфные графы, полученные из G1 путем подразбиения ребер G1

Граф К5 – полный граф с 5 вершинами
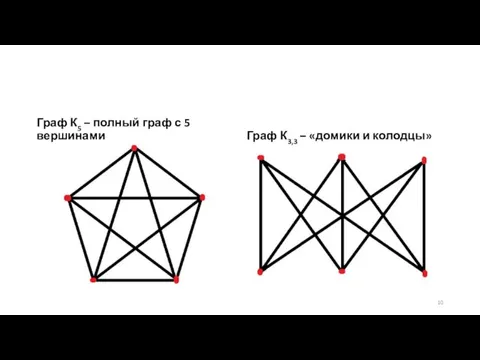
Граф К3,3 – «домики и колодцы»

Примеры гомеоморфных графов

Вопрос о распознавании планарности графа являлся в свое время серьезной математической проблемой, которую на сегодняшний день удалось решить.

Некоторые критерии планарности графов
Теорема Понтрягина-Куратовского. Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K5 или K3,3.
Теорема
Граф планарен тогда и только тогда, когда в нем нет подграфов, стягиваемых (т.е. получаемых последовательностью отождествлений вершин, связанных ребрами) к графам K5 или K3,3.

Для непланарных графов вводятся характеристики, представляющие ту или иную меру непланарности.
Если граф непланарен, то для его геометрической реализации удаляют отдельные ребра – переносят их на другую плоскость.
Наименьшее число ребер, удаление которых приводит к планарному графу, называется числом планарности или искаженностью графа G и обозначается sk(G)

Для числа планарности полного графа справедлива следующая формула:
n≥3

n=4
G – полный граф, является планарным

N=5
G – полный граф, не является планарным

Примеры из практики. В электротехнике части цепей наносятся на одну сторону непроводящей пластины (печатная плата). Поскольку проводники не изолированы, они не могут пересекаться, и соответствующие графы должны быть планарными.
Требуется знать, сколько печатных плат понадобится для формирования всей сети.
С этой целью вводится понятие толщины графа.
Толщина графа t(G) – наименьшее число планарных графов, наложение которых дает G.

Толщина графа является мерой его «непланарности».
Например, толщина планарного графа равна единице, поскольку его можно разместить на одной плоскости.
t(K5)=2 и t(K3,3)=2

Оценку снизу для толщины графа можно получить по теореме Эйлера.
Это довольно грубая оценка.
Однако часто оказывается истинным значением толщины графа.
Обозначения:
[x] – наибольшее целое число, не превосходящее x,
{x} – наименьшее целое число, не превосходящее x

Теорема о нижней границе толщины графа
Толщина t(G) графа G удовлетворяет следующим неравенствам:
n – количество вершин, m – количество ребер графа G

2. Укладка графа на плоскости
Критерии планарности не всегда просты в практическом применении. Также они не дают информации о том, как выполнить укладку планарного графа на плоскости.
Рассмотрим некоторые алгоритмы проверки планарности графа и построения его плоской укладки.

Алгоритм представляет собой процесс последовательного присоединения к некоторому уложенному подграфу G’ графа G новой цепи L, оба конца которой принадлежат G.
Затем в качестве подграфа G’ выбирается любой простой цикл графа G, и процесс присоединения новых цепей продолжается до тех пор, пока не будет построен плоский граф, изоморфный G.
Либо присоединение новой простой цепи на некотором этапе окажется невозможным. Что будет свидетельствовать о непланарности исходного графа G.

Пусть имеется некоторая плоская укладка подграфа G’ = (V’, E’) графа G = (V, E).
Сегментом Gi относительно G’ называется подграф графа G следующих двух видов:
ребро e = (u, v) такое, что e ∉E’ , u, v ∈ V’;
Связная компонента графа G \ G’ , дополненная всеми ребрами графа G, соединяющими эту компоненту с подграфом G’, и концами этих ребер.

Вершина u сегмента Gi называется контактной, если u ∈ V’
Граф G’ – плоский, значит, он разбивает плоскость на грани. Допустимой гранью для сегмента Gi относительно G’ называется грань Г графа G’, содержащая все контактные вершины сегмента Gi

Обозначим через Γ(Gi) множество допустимых граней для Gi .
Для непланарных графов может быть Γ(Gi) = ∅.
Рассмотрим простую цепь L сегмента Gi, соединяющую две контактные вершины этого сегменты и не содержащую других контактных вершин.
Такие цепи называются α-цепями.
Всякая α-цепь может быть уложена в любую грань, допустимую для данного сегмента.

Два сегмента Gi и Gj называются конфликтующими, если:
θ = Γ(Gi) ∩ Γ(Gj) ≠ ∅;
существуют две α-цепи Li ∈ Gi и Lj ∈ Gj, которые нельзя уложить без пересечений одновременно ни в какую грань Г ∈ θ.

Пусть G’ – плоская укладка некоторого подграфа графа G.
Для каждого сегмента Gi относительно G’ находим множество допустимых граней.
Тогда возможны следующие случаи:
А) существует сегмент Gi, для которого Γ(Gi) = ∅, тогда исходный граф G непланарен;
Б) для некоторого сегмента Gi существует единственная допустимая грань Γ, тогда располагаем любую α-цепь сегмента Gi в грани Γ, при этом грань Γ разобьется на две грани;
В) Γ(Gi) ≥ 2 для всех Gi, тогда располагаем любую α-цепь сегмента Gi в любой допустимой грани.
Если на очередном шаге множество сегментов пусто, то построена укладка графа на плоскости.

Алгоритм укладки планарного графа на плоскости
Шаг 1. Выбираем любой простой цикл С графа G. Укладываем этот цикл на плоскости и полагаем G’ = C.
Шаг 2. Находим все грани графа G’ и все сегменты Gi относительно G’. Если множество сегментов пусто, то укладка графа G на плоскости построена, конец алгоритма.
Шаг 3. Для каждого сегмента Gi определяем множество допустимых граней Γ(Gi). Если найдется сегмент Gi, для которого Γ(Gi) = ∅, то исходный граф непланарен, конец алгоритма. Иначе переход на шаг 4.

Шаг 4. Если существует сегмент Gi, для которого имеется единственная допустимая грань С, то переход на шаг 6. Иначе на шаг 5.
Шаг 5. Для некоторого сегмента Gi , для которого Г(Gi)>1, выбираем произвольную допустимую грань Г.
Шаг 6. Произвольная α-цепь L сегмента Gi помещаем в грань Г. Полагаем G’ = G’ ∪ L и переход на шаг 1.
Шаг 7. Построена укладка G’ графа G. Конец алгоритма.

Замечание
Любой планарный граф можно уложить на сфере, и обратно.
⇒ планарный граф можно уложить на плоскости несколькими способами.

Пример. Выполнить укладку графа на плоскости
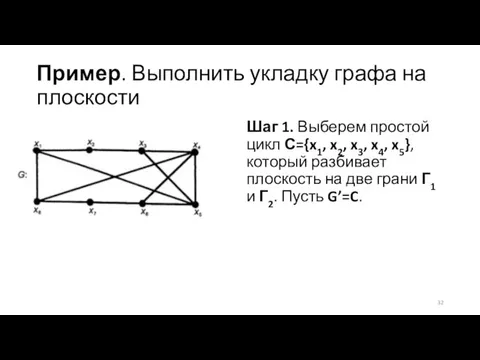
Шаг 1. Выберем простой цикл С={x1, x2, x3, x4, x5}, который разбивает плоскость на две грани Г1 и Г2. Пусть G’=C.

Шаг 2. На рисунке показан граф G’=C и сегменты G1 и G2 исходного графа G относительно G’. Контактные вершины обведены кружками.
Г(Gi)={Г1, Г2}, i=1, 2.
Шаг 3. Г(Gi)≠∅, i=1, 2.
Шаг 4. Нет сегмента, для которого бы существовала единственная допустимая грань.
Шаг 5. Любую α-цепь можно уложить в Г1 или Г2. Выберем для укладки грань Г1.

Шаг 6. Пусть L={x1, x8, x7, x6, x5}.
Поместим эту α-цепь в Г1. Возникает новый граф G’ и его сегменты G1, G2, G3. появляется новая грань Г3.
Переходим к шагу 1

Шаг 1. Имеем новые сегменты G1, G2, G3.
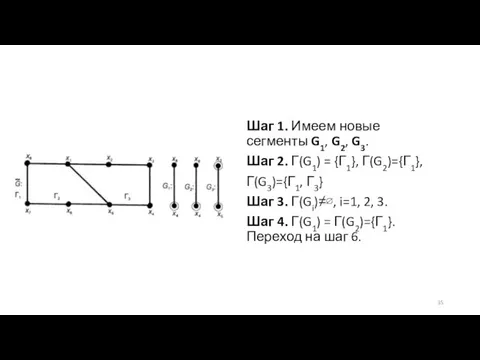
Шаг 2. Г(G1) = {Г1}, Г(G2)={Г1},
Г(G3)={Г1, Г3}
Шаг 3. Г(Gi)≠∅, i=1, 2, 3.
Шаг 4. Г(G1) = Г(G2)={Г1}. Переход на шаг 6.

Шаг 6. α-цепь L1={x4, x8} поместим в грань Г1, α-цепь L2={x4, x6} также поместим в эту грань.
В результате возникает новый граф G’. Он имеет пять граней и один сегмент.

Шаг 1. G1 – ребро (x3, x5).
Шаг 2. Г(G1)={Г3}
Шаг 3. Г(G1)≠∅
Шаг 4. Г(G1)={Г3}, переход на шаг 6
Шаг 6. α-цепь L1={x3, x5} поместим в грань Г3. Новый граф G’ является плоской укладкой исходного планарного графа.