такой цикл (замкнутый путь), который проходит через каждую вершину данного графа ровно по одному разу[2]; то есть простой цикл, в который входят все вершины графа.
Также с гамильтоновым графом тесно связано понятие гамильтонова пути, который является простым путём (путём без петель), проходящим через каждую вершину графа ровно один раз[1]. Гамильтонов путь отличается от цикла тем, что у пути начальные и конечные точки могут не совпадать, в отличие от цикла. Гамильтонов цикл является гамильтоновым путём.
Гамильтоновы путь, цикл и граф названы в честь ирландского математика У. Гамильтона, который впервые определил эти классы, исследовав задачу «кругосветного путешествия» по додекаэдру. В этой задаче вершины додекаэдра символизировали известные города, такие как Брюссель, Амстердам, Эдинбург, Пекин, Прага, Дели, Франкфурт и др., а рёбра — соединяющие их дороги. Путешествующий должен пройти «вокруг света», найдя путь, который проходит через все вершины ровно один раз[3]. Чтобы сделать задачу более интересной, порядок прохождения городов устанавливался заранее. А чтобы было легче запомнить, какие города уже соединены, в каждую вершину додекаэдра был вбит гвоздь, и проложенный путь отмечался небольшой верёвкой, которая могла обматываться вокруг гвоздя. Однако такая конструкция оказалась слишком громоздкой, и Гамильтон предложил новый вариант игры, заменив додекаэдр плоским графом, изоморфным графу, построенному на рёбрах додекаэдра[4].
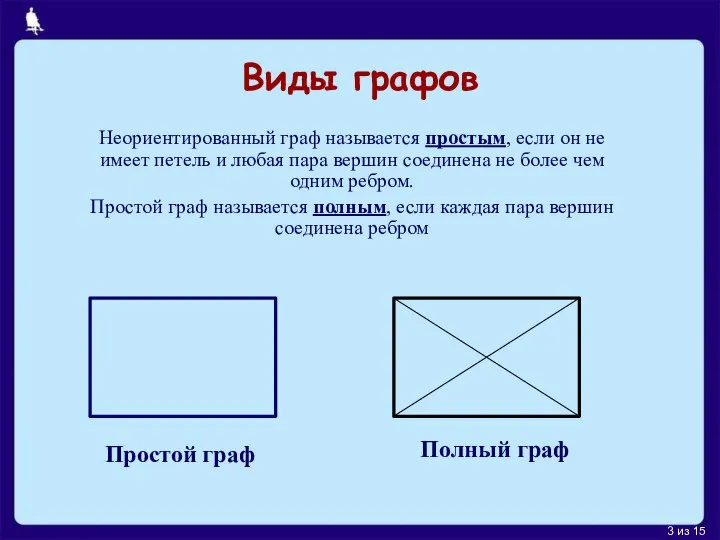
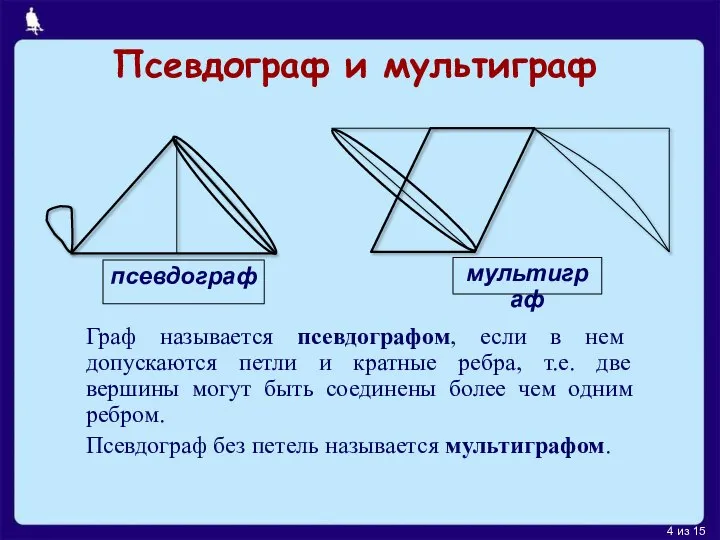
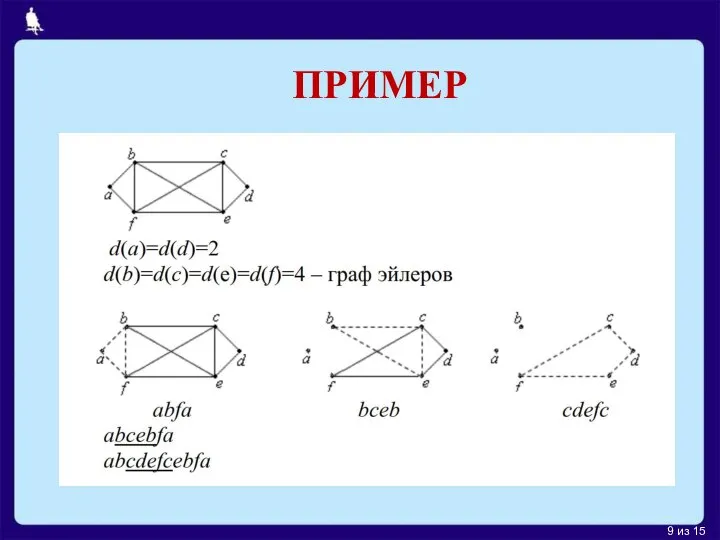
Гамильто́нов граф — граф, содержащий гамильтонов цикл.
При этом гамильтоновым циклом является такой цикл (замкнутый путь), который проходит через каждую вершину данного графа ровно по одному разу; то есть простой цикл, в который входят все вершины графа.
Также с гамильтоновым графом тесно связано понятие гамильтонова пути, который является простым путём (путём без петель), проходящим через каждую вершину графа ровно один раз. Гамильтонов путь отличается от цикла тем, что у пути начальные и конечные точки могут не совпадать, в отличие от цикла. Гамильтонов цикл является гамильтоновым путём.



![Гамильтоновы графы амильто́нов граф — граф, содержащий гамильтонов цикл[1]. При этом гамильтоновым](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/989689/slide-9.jpg)
![Гамильтоновы графы амильто́нов граф — граф, содержащий гамильтонов цикл[1]. При этом гамильтоновым](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/989689/slide-10.jpg)






 Статистика. Введение в теорию вероятности. Основные понятия
Статистика. Введение в теорию вероятности. Основные понятия Доказательство тождеств
Доказательство тождеств Построение сечений многогранников
Построение сечений многогранников Задачи на призму
Задачи на призму Сложение и вычитание чисел в пределах 20
Сложение и вычитание чисел в пределах 20 Тетраэдр
Тетраэдр Декартова система координат
Декартова система координат Презентация на тему Простейшие задачи в координатах (9 класс)
Презентация на тему Простейшие задачи в координатах (9 класс)  Уравнения математической физики
Уравнения математической физики Сложение и вычитание трехзначных чисел
Сложение и вычитание трехзначных чисел Готовимся к ОГЭ. Математика
Готовимся к ОГЭ. Математика Тренажёр Единицы измерени времени
Тренажёр Единицы измерени времени Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Математика. Решение задач
Математика. Решение задач Переместительное свойство умножения
Переместительное свойство умножения Степень с натуральным показателем
Степень с натуральным показателем Деление числа на десятичную дробь
Деление числа на десятичную дробь Презентация на тему Математический КВН
Презентация на тему Математический КВН  Деление десятичных дробей
Деление десятичных дробей Линейные модели в задачах регрессии
Линейные модели в задачах регрессии Пересечение поверхностей
Пересечение поверхностей Презентация по математике "Перестановка слагаемых" -
Презентация по математике "Перестановка слагаемых" -  Теория погрешностей
Теория погрешностей Проектирование разноритмичных и неритмичных потоков
Проектирование разноритмичных и неритмичных потоков Непрерывные случайные величины
Непрерывные случайные величины Открытый урок по алгебре в 8 классе
Открытый урок по алгебре в 8 классе Экономический факторный анализ. Теорема о среднем
Экономический факторный анализ. Теорема о среднем Элементы теории вероятностей
Элементы теории вероятностей