Содержание
- 2. LECTURE 6 Probability Temur Makhkamov Indira Khadjieva QM Module Leaders [email protected] [email protected] Office hours: by appointment
- 3. Lecture outline The meaning of probability and relevant concepts The basic operations of probability Sets, combination,
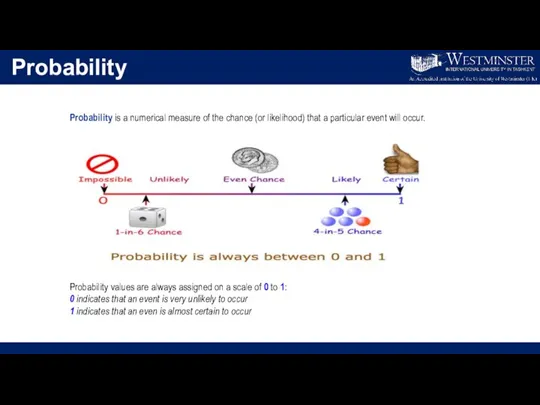
- 4. Probability Probability is a numerical measure of the chance (or likelihood) that a particular event will
- 5. Experiment vs Sample Space The probability is a chance or likelihood of an event to happen
- 6. Experiment vs Sample Space
- 7. Experiment vs Sample Space
- 8. Calculation of probability There are 6 blue, 3 red, 2 yellow, and 1 green marbles in
- 9. Calculation of probability There are 6 blue, 3 red, 2 yellow, and 1 green marbles in
- 10. Calculation of probability If there are n experimental outcomes, the sum of the probabilities for all
- 12. Types of counting rules Multiple step Combination Permutation
- 13. Multiple step experiment Experiment of a sequence of k steps Total number of experimental outcomes is
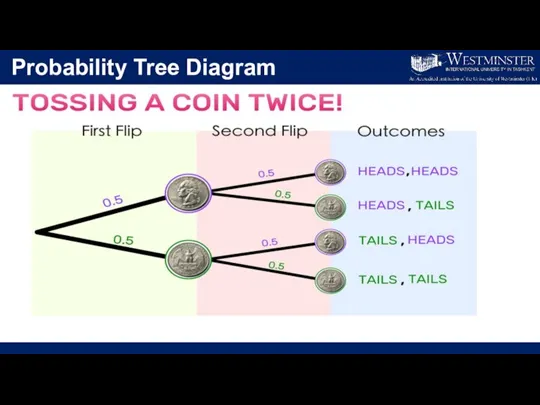
- 14. Probability Tree Diagram
- 15. Probability Tree Diagram
- 16. Probability calculation
- 17. Self exam-training task: Find the number of all possible outcomes for rolling a die three times
- 18. Combination Example: In this classroom, a lecturer randomly picks two of five students (let’s say Shakhzoda,
- 19. Combination Combination formula: n objects are to be selected from a set of N objects, where
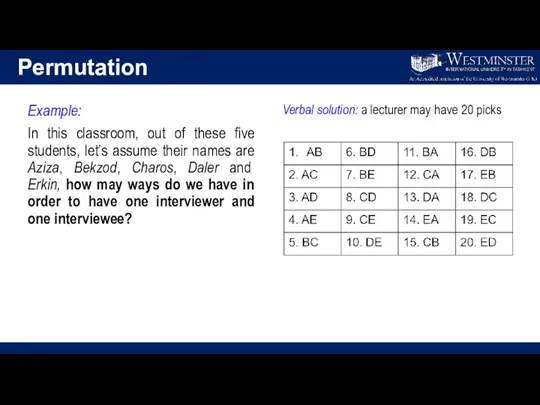
- 20. Permutation Example: In this classroom, out of these five students, let’s assume their names are Aziza,
- 21. Permutation Permutation formula: n objects are to be selected from a set of N objects, where
- 22. What Permutation can tell us ?
- 23. Operations with events The union of events A and B is the event containing all experimental
- 24. Operations with events Toss a die and observe the number that appears on top S =
- 25. Relationship of events Mutually exclusive events - The events A and B do not have any
- 26. Addition rule for union Question: On Quantitative Methods module for 600 CIFS students at WIUT, 480
- 27. Multiplication rule for intersection
- 28. Multiplication Rule A bowl contains 7 red marbles and 3 black marbles. Two marbles are drawn
- 29. Solution Let A = the event that the first marble is black; let B = the
- 30. Mathematical expectation 365bet.com sent you following offers for coming El-Classico game depending on your betting: If
- 31. Concluding remarks Today, you learned: Basic concepts within probability theory Basic operations of calculating the sample
- 33. Скачать презентацию



























 Процент
Процент Решение задач. Подготовка к умножению
Решение задач. Подготовка к умножению Цилиндр. Задачи
Цилиндр. Задачи Деление многочленов
Деление многочленов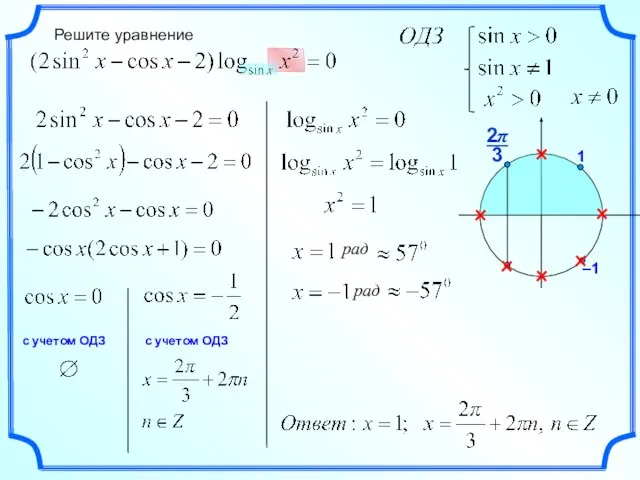 Решение уравнения
Решение уравнения Десятичные дроби. 5 класс
Десятичные дроби. 5 класс Исследование функций и построение графиков
Исследование функций и построение графиков Квадрат. Свойства и признаки квадрата
Квадрат. Свойства и признаки квадрата Треугольник и его виды
Треугольник и его виды Создание системы внеклассной работы в физико-математическом образовании
Создание системы внеклассной работы в физико-математическом образовании Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница
Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница Решение задач. Периметр и площадь
Решение задач. Периметр и площадь Морской бой
Морской бой Презентация на тему Решение задач на пропорциональное деление (4 класс)
Презентация на тему Решение задач на пропорциональное деление (4 класс)  Задачи предельного типа
Задачи предельного типа Уравнения математической физики
Уравнения математической физики Метод следов. Построение следа секущей плоскости
Метод следов. Построение следа секущей плоскости Вычитание числа 2 (1 класс)
Вычитание числа 2 (1 класс)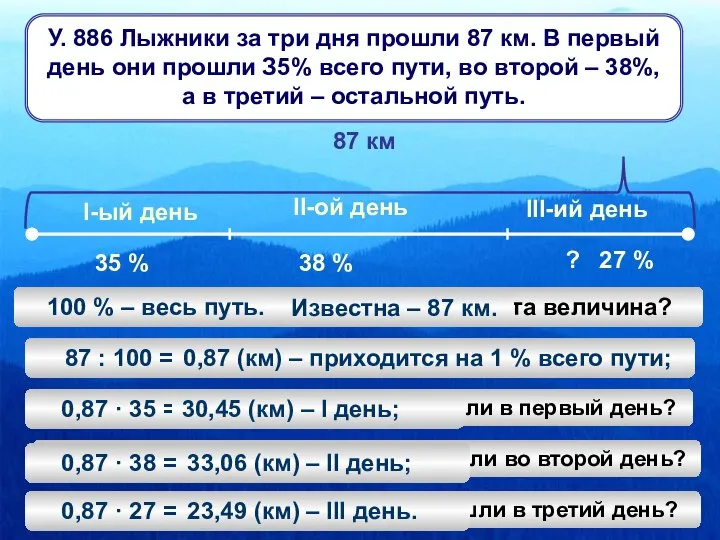 Задачи о лыжниках
Задачи о лыжниках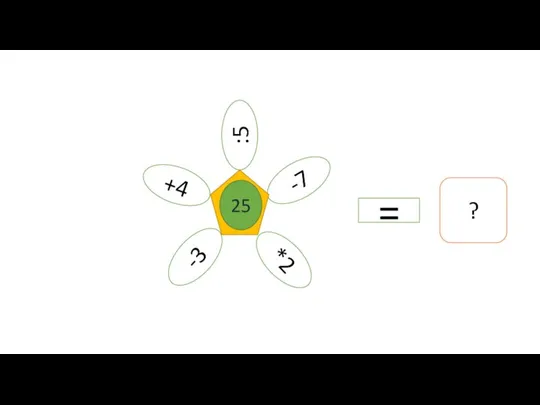 Ромашка
Ромашка Графики уравнений. Преобразование графиков уравнений, содержащих модуль
Графики уравнений. Преобразование графиков уравнений, содержащих модуль Узагальнення і систематизація матеріалу по дробам
Узагальнення і систематизація матеріалу по дробам Объем пирамиды
Объем пирамиды Волшебное число ПИ
Волшебное число ПИ Precvičujeme. Správne riešenia
Precvičujeme. Správne riešenia Точки экстремума
Точки экстремума Системы уравнений
Системы уравнений Сравнительный анализ методов полиэдральной аппроксимации при построении гарантирующего решения
Сравнительный анализ методов полиэдральной аппроксимации при построении гарантирующего решения