Содержание
- 2. Определение производной Пусть функция y = f(x) определена в некотором интервале (a; b). Аргументу x придадим
- 3. Определение производной Итак, по определению: Функция y = f(x) , имеющая производную в каждой точке интервала
- 4. Геометрический смысл производной Возьмем на непрерывной кривой L две точки М и М1: х f(x )
- 5. Геометрический смысл производной Производная f ’(x) равна угловому коэффициенту касательной к графику функции y = f(x)
- 6. Связь между непрерывностью и дифференцируемостью функции Если функция f(x) дифференцируема в некоторой точке , то она
- 7. Производные основных элементарных функций 1 Формула бинома Ньютона: Степенная функция: K – факториал
- 8. Производные основных элементарных функций По формуле бинома Ньютона имеем: Тогда:
- 9. Производные основных элементарных функций 2 Логарифмическая функция: Аналогично выводятся правила дифференцирования других основных элементарных функций.
- 10. Правила дифференцирования Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b) функции,
- 11. Производная сложной функции Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x))
- 12. Пример Вычислить производную функции
- 14. Скачать презентацию








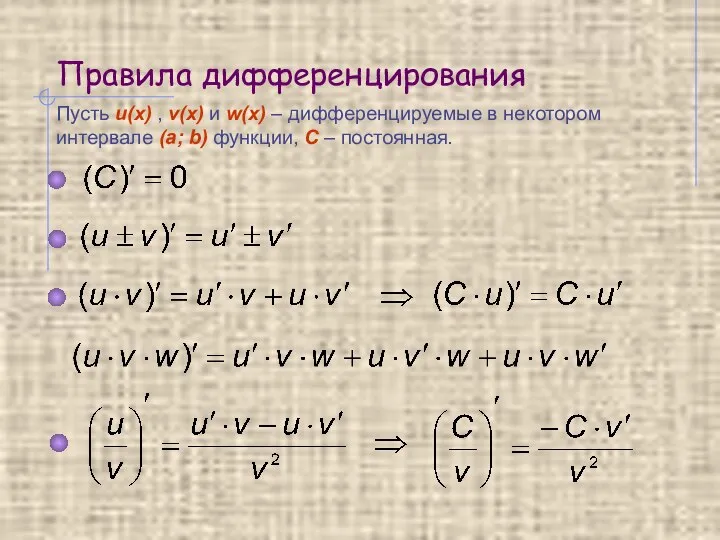


 Опорні конспекти на уроках математики
Опорні конспекти на уроках математики Координатная плоскость. Графики
Координатная плоскость. Графики презентация
презентация Действия со степенями. Корень n-ой степени. Степень с рациональным показателем
Действия со степенями. Корень n-ой степени. Степень с рациональным показателем Сложение и вычитание. Закрепление. Урок математики, 1 класс
Сложение и вычитание. Закрепление. Урок математики, 1 класс Последовательности и прогрессии (ПР №25)
Последовательности и прогрессии (ПР №25) Деление чисел
Деление чисел Презентация по математике "Математический язык" -
Презентация по математике "Математический язык" -  Построение графиков функций
Построение графиков функций Объединение серий измерений
Объединение серий измерений Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Математическая логика
Математическая логика Элементы теории множеств
Элементы теории множеств Формулы корней квадратных уравнений
Формулы корней квадратных уравнений Принципы статистического оценивания. Анализ данных
Принципы статистического оценивания. Анализ данных Определитель и его свойства
Определитель и его свойства Множественная регрессия и корреляция
Множественная регрессия и корреляция Построение асимптотических ЛАЧХ и ЛФЧХ для передаточных функций общего вида
Построение асимптотических ЛАЧХ и ЛФЧХ для передаточных функций общего вида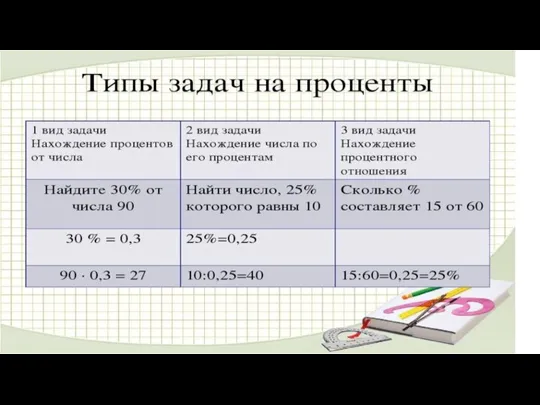 Задачи на проценты
Задачи на проценты Вычисление производной степенной
Вычисление производной степенной Частные производные
Частные производные Презентация на тему Связь математики с другими науками
Презентация на тему Связь математики с другими науками  Игра-тренажёр. Весёлые снежинки. (1 класс)
Игра-тренажёр. Весёлые снежинки. (1 класс) Решение тестовых задач. Готовимся к ЕГЭ
Решение тестовых задач. Готовимся к ЕГЭ Связь между компонентами и результатом умножения. Чётные и нечётные числа
Связь между компонентами и результатом умножения. Чётные и нечётные числа Показательная функция
Показательная функция Разновидности многогранников
Разновидности многогранников Физические величины
Физические величины