Содержание
- 2. Проблема Тема “Разные задачи на многогранники, цилиндр, конус и шар” является одной из самых сложных в
- 3. Технология проекта Целью своего проекта ставлю: формирование устойчивого интереса к предмету геометрия, повышения качества знаний учащихся.
- 4. Актуальность проекта Если школа не идет в ногу с жизнью, то учащиеся «перестают ее уважать, перестают
- 5. Актуальность проекта Применение презентаций обеспечивает получение большего объема информации за короткий период, всегда можно вернуться к
- 6. Содержание Предисловие Многогранники, вписанные в шар Основные определения и теоремы Вопросы Примеры решения задач Многогранники, описанные
- 7. Предисловие Материал представлен по следующему плану: основные теоретические сведения (могут быть предложены учащимся для записи, т.
- 8. Многогранники, вписанные в шар Основные определения и теоремы Определение. Сфера называется описанной около многогранника (или многогранник,
- 9. Призма Теорема Около призмы можно описать сферу тогда и только тогда, когда призма прямая и около
- 10. Ответим устно! Можно ли описать сферу (шар) около: а) куба; б) прямоугольного параллелепипеда; в) наклонного параллелепипеда,
- 11. Ответим устно! Около треугольной призмы описана сфера, центр которой лежит вне призмы. Какой треугольник является основанием
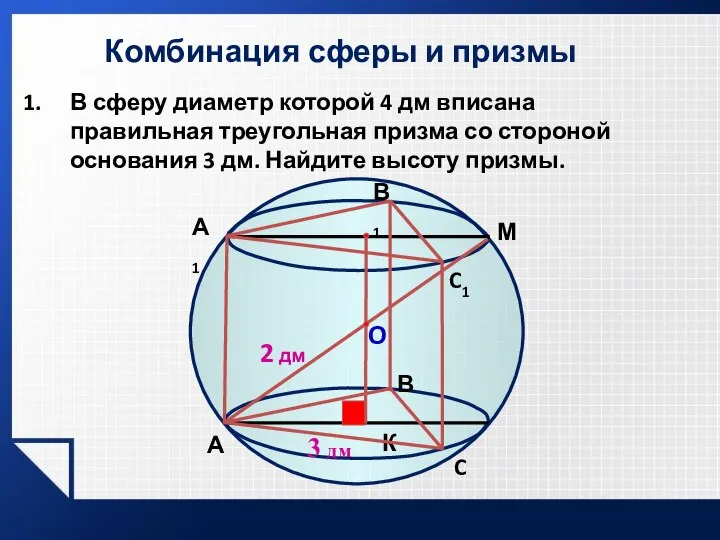
- 12. Комбинация сферы и призмы В сферу диаметр которой 4 дм вписана правильная треугольная призма со стороной
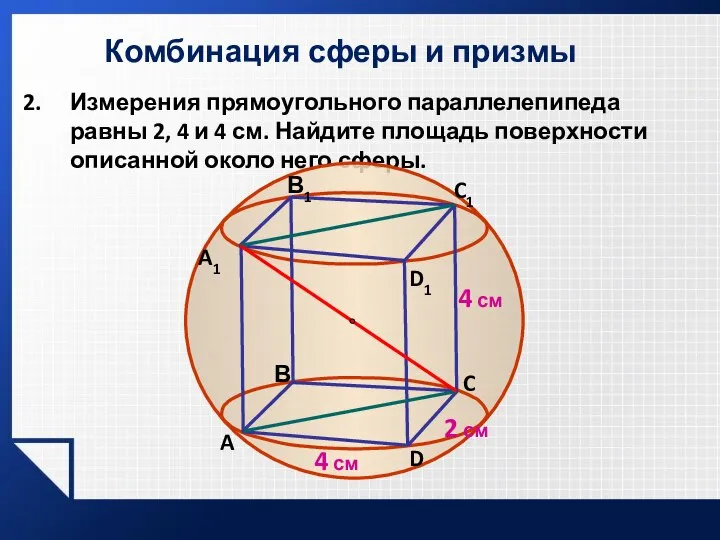
- 13. Комбинация сферы и призмы Измерения прямоугольного параллелепипеда равны 2, 4 и 4 см. Найдите площадь поверхности
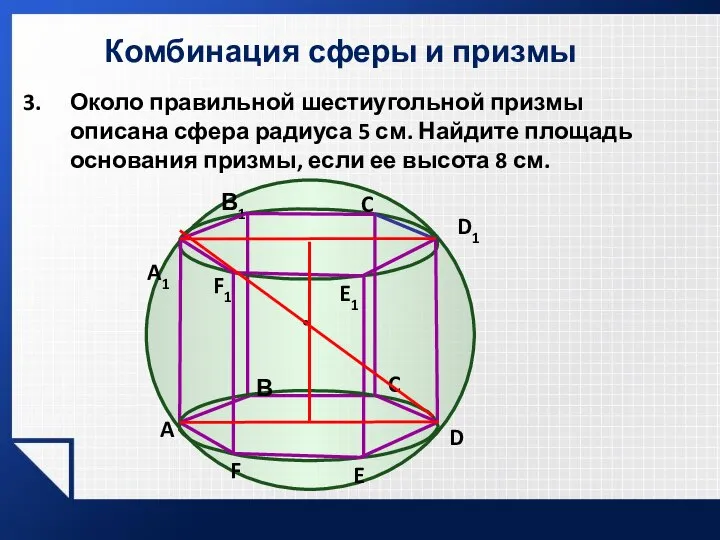
- 14. Комбинация сферы и призмы Около правильной шестиугольной призмы описана сфера радиуса 5 см. Найдите площадь основания
- 15. Комбинация сферы и призмы Из учебника Л.С.Атанасяна № 637(а), №639(а,б)
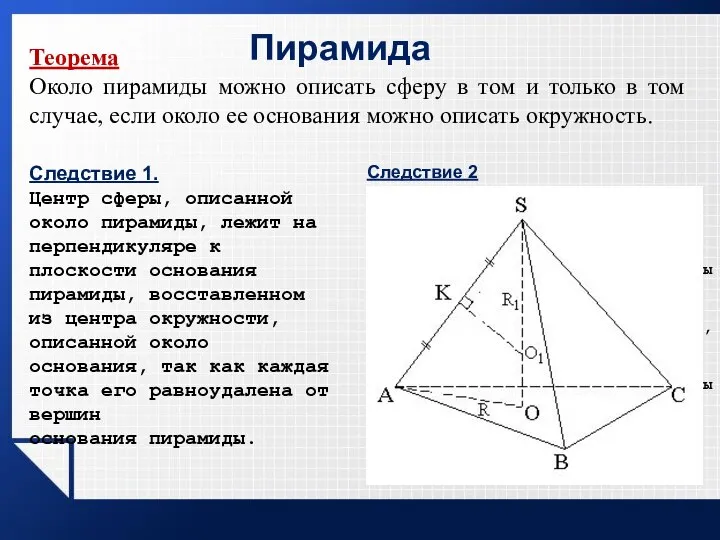
- 16. Пирамида Теорема Около пирамиды можно описать сферу в том и только в том случае, если около
- 17. Ответим устно! Справедливо ли утверждение, что около любой треугольной пирамиды можно описать сферу? Можно ли описать
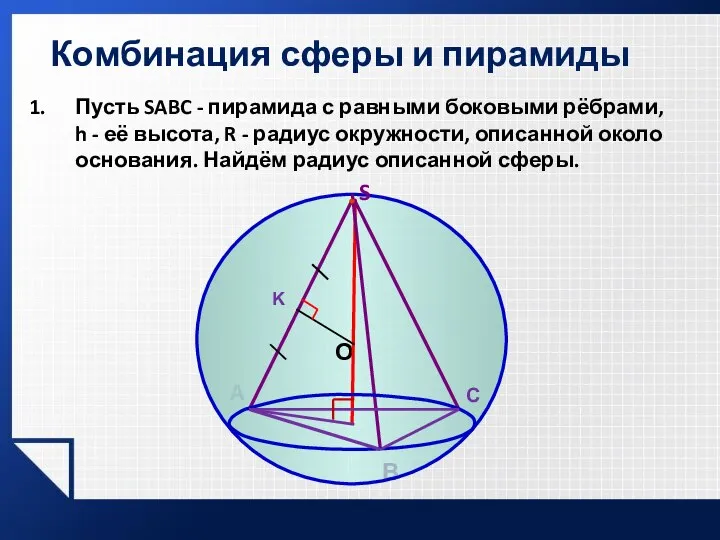
- 18. Пусть SABC - пирамида с равными боковыми рёбрами, h - её высота, R - радиус окружности,
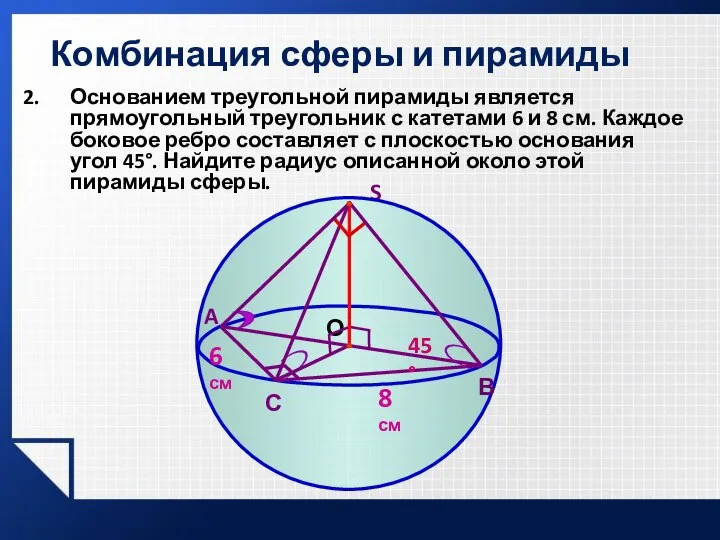
- 19. Комбинация сферы и пирамиды Основанием треугольной пирамиды является прямоугольный треугольник с катетами 6 и 8 см.
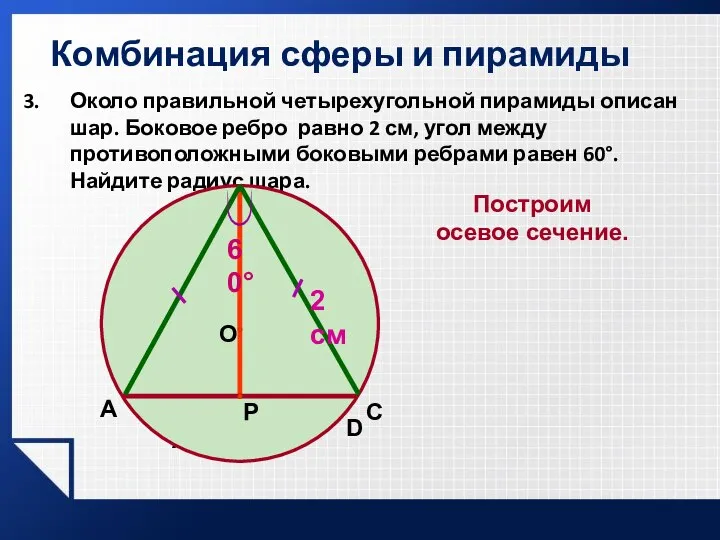
- 20. Комбинация сферы и пирамиды Около правильной четырехугольной пирамиды описан шар. Боковое ребро равно 2 см, угол
- 21. Комбинация сферы и пирамиды Из учебника Л.С.Атанасяна № 637(б), №639(в)
- 22. Многогранники, описанные около шара Основные определения и теоремы Определение. Сфера называется вписанной в многогранник, если все
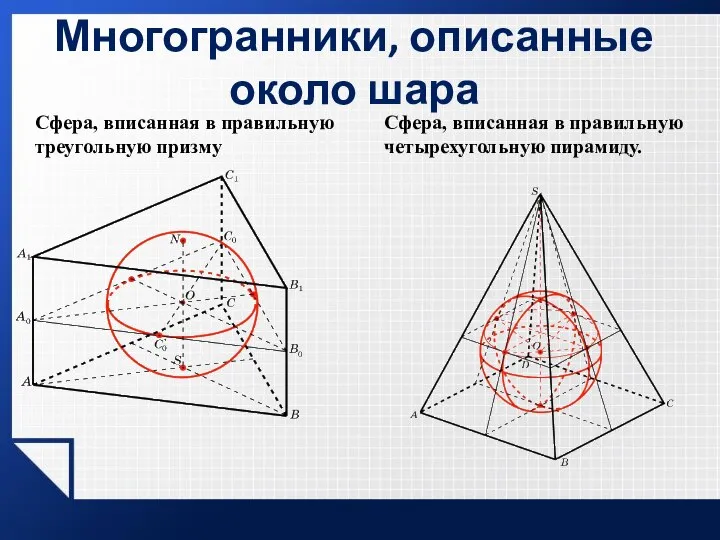
- 23. Многогранники, описанные около шара Сфера, вписанная в правильную треугольную призму Сфера, вписанная в правильную четырехугольную пирамиду.
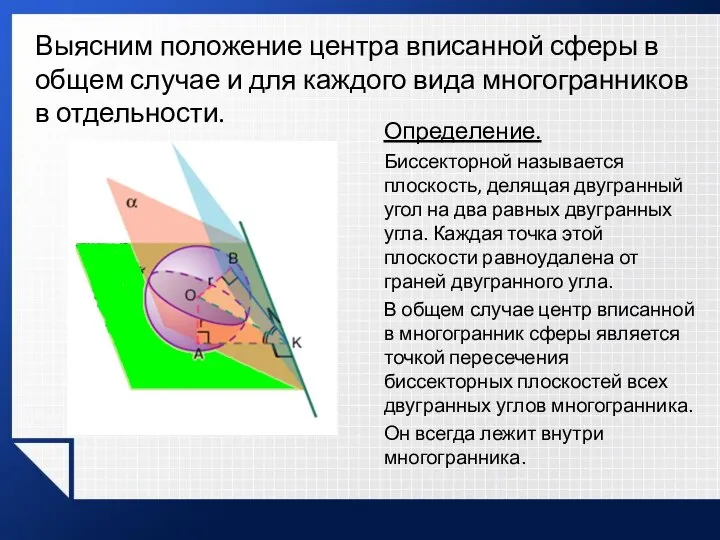
- 24. Выясним положение центра вписанной сферы в общем случае и для каждого вида многогранников в отдельности. Определение.
- 25. Призма Теорема. Шар можно вписать в прямую призму в том и только в том случае, если
- 26. Ответим устно! Каким свойством должна обладать прямая призма, чтобы в нее можно было вписать сферу? В
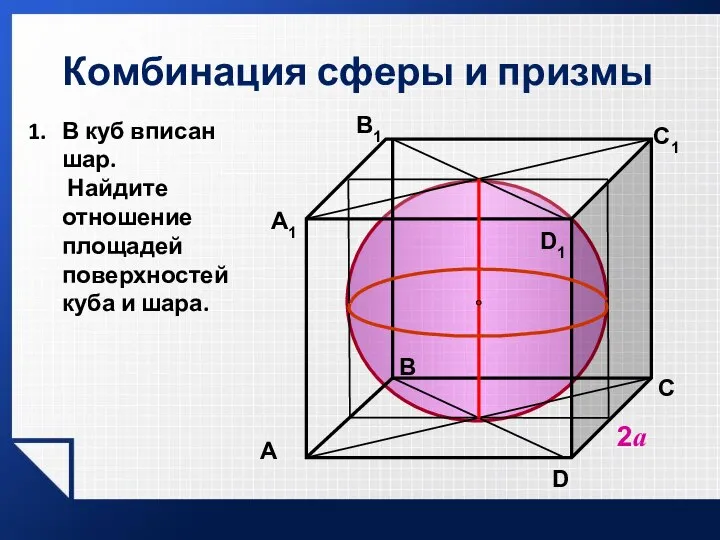
- 27. Комбинация сферы и призмы 2а В C D1 A1 В1 C1 A D В куб вписан
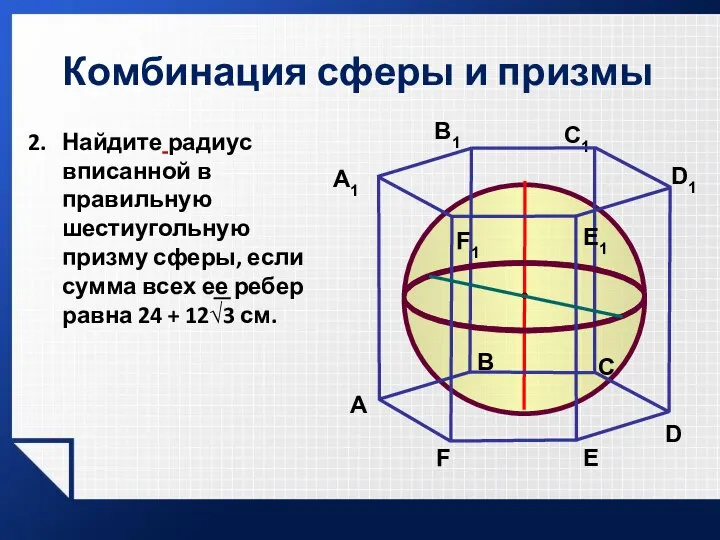
- 28. Комбинация сферы и призмы A В C A1 В1 C1 E1 F1 E F Найдите радиус
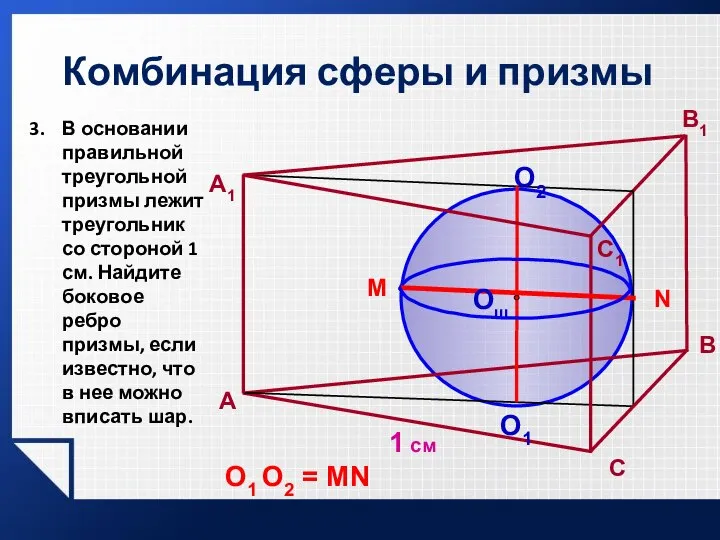
- 29. Комбинация сферы и призмы 1 см A В A1 C1 Oш O2 O1 N M О1
- 30. Комбинация сферы и призмы Из учебника Л.С.Атанасяна № 632.
- 31. Пирамида Теорема. Если боковые грани пирамиды одинаково наклонены к основанию, то в такую пирамиду можно вписать
- 32. Ответим устно! Приведите пример пирамиды, в которую нельзя вписать сферу? При каком условии в правильную четырехугольную
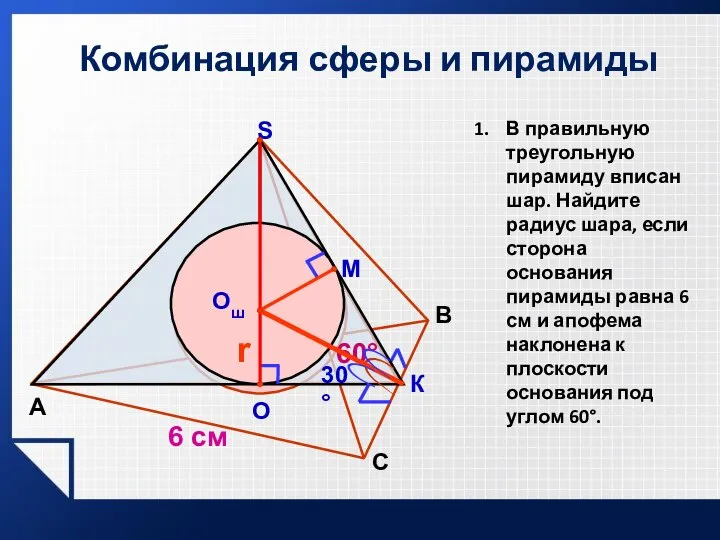
- 33. Комбинация сферы и пирамиды А B S М К Oш r 60° О 6 см 30°
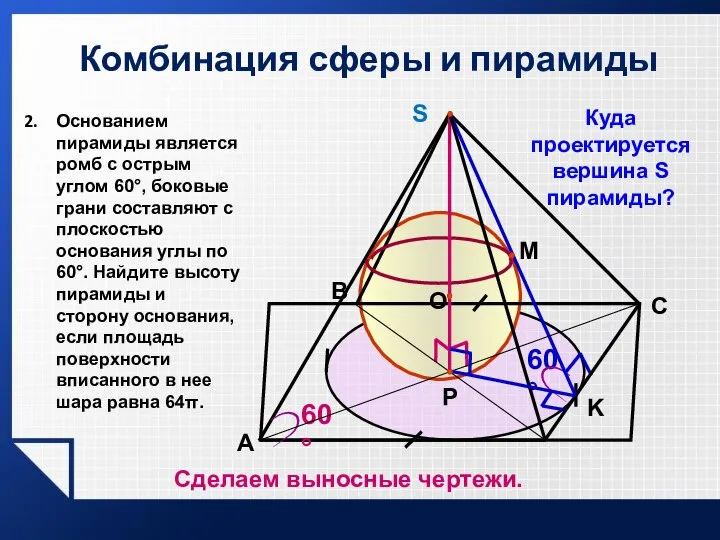
- 34. Комбинация сферы и пирамиды 60° A P K 60° C B Куда проектируется вершина S пирамиды?
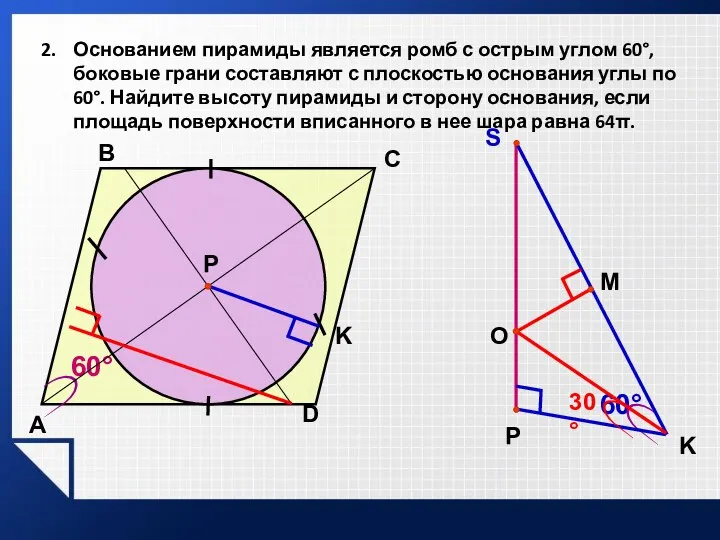
- 35. Основанием пирамиды является ромб с острым углом 60°, боковые грани составляют с плоскостью основания углы по
- 36. Комбинация сферы и пирамиды Из учебника Л.С.Атанасяна № 635, №638 (б), №640, №641.
- 37. Шар, описанный около правильной усеченной пирамиды. Теорема . Около любой правильной усеченной пирамиды можно описать шар.
- 38. Ответим устно! При каком условии в правильную четырехугольную усеченную пирамиду можно вписать сферу? В треугольную усеченную
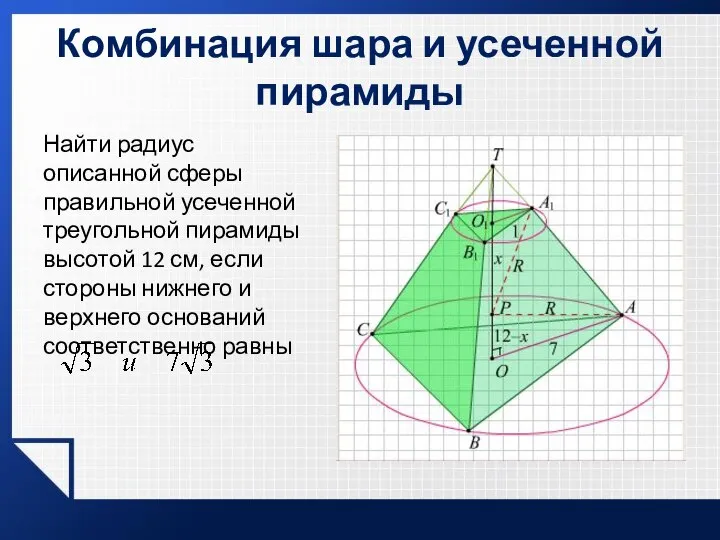
- 39. Комбинация шара и усеченной пирамиды Найти радиус описанной сферы правильной усеченной треугольной пирамиды высотой 12 см,
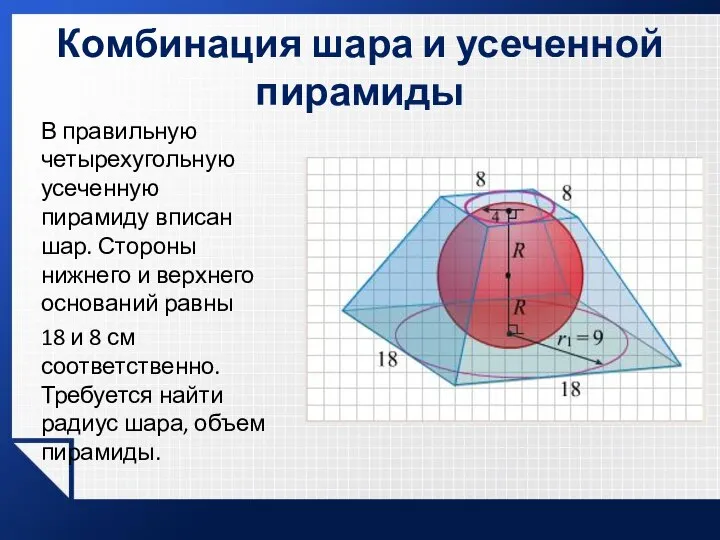
- 40. Комбинация шара и усеченной пирамиды В правильную четырехугольную усеченную пирамиду вписан шар. Стороны нижнего и верхнего
- 41. Из учебника Л.С.Атанасяна № 636. Комбинация шара и усеченной пирамиды
- 42. Комбинация шара с круглыми телами Теорема. Около цилиндра, усеченного конуса (прямых круговых), конуса можно описать шар.
- 43. Ответим устно! Можно ли описать сферу около цилиндра (прямого кругового)? Можно ли описать сферу около конуса,
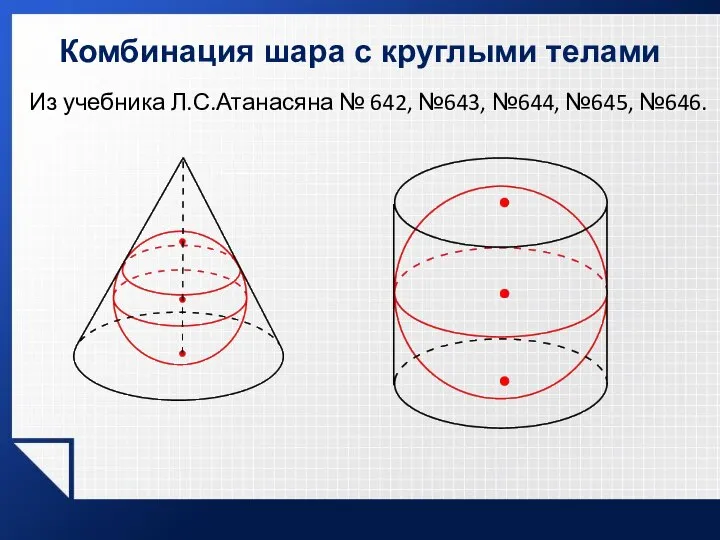
- 44. Из учебника Л.С.Атанасяна № 642, №643, №644, №645, №646. Комбинация шара с круглыми телами
- 45. Заключение На изучение темы «Разные задачи на многогранники, цилиндр, конус и шар» по планированию отводятся три
- 46. Заключение Диаграмма отражает сравнение результатов самостоятельной работы, проведенной после изучения данной темы в двух классах 11
- 47. Заключение Использование компьютера на уроках – это не дань моде, не способ переложить на плечи компьютера
- 49. Скачать презентацию




























 Основы дисперсионного анализа
Основы дисперсионного анализа Анализ задач и альтернативные методы решений. Мастер-класс
Анализ задач и альтернативные методы решений. Мастер-класс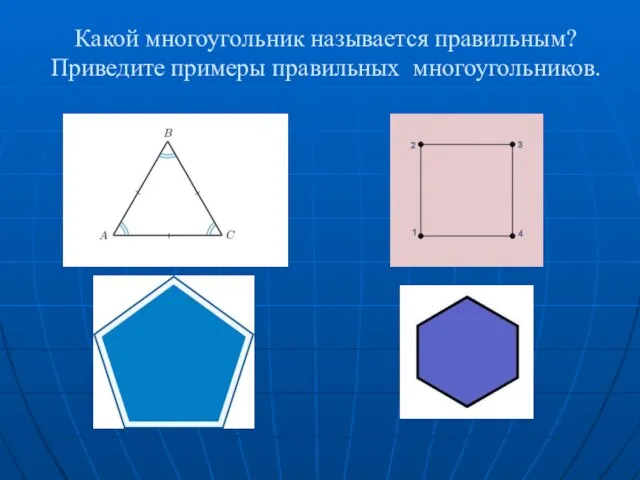 Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Подборка заданий по геометрии за курс 7 класса
Подборка заданий по геометрии за курс 7 класса Предел последовательности. Практическая работа № 24
Предел последовательности. Практическая работа № 24 Построение графиков функций
Построение графиков функций Косинус острого угла прямоугольного треугольника
Косинус острого угла прямоугольного треугольника Презентация на тему УМНОЖЕНИЕ ДРОБЕЙ
Презентация на тему УМНОЖЕНИЕ ДРОБЕЙ  Sıralama algoritmaları
Sıralama algoritmaları Вычисление определенных интегралов (Занятие №6)
Вычисление определенных интегралов (Занятие №6) Презентация на тему Прямоугольные треугольники
Презентация на тему Прямоугольные треугольники  Вероятность. Задачи
Вероятность. Задачи Метод итераций
Метод итераций Сложение и вычитание в пределах 100
Сложение и вычитание в пределах 100 Презентация на тему Нахождение процента от числа
Презентация на тему Нахождение процента от числа  Поверхности второго порядка
Поверхности второго порядка Схемы к задачам
Схемы к задачам Меры измерения времени
Меры измерения времени Презентация на тему Прямоугольный параллелепипед и его свойства
Презентация на тему Прямоугольный параллелепипед и его свойства  Сведения об объеме эфирного времени, затраченного на освещение деятельности политических партий в июле 2020 года
Сведения об объеме эфирного времени, затраченного на освещение деятельности политических партий в июле 2020 года Единицы объёма. Задания
Единицы объёма. Задания Задачи
Задачи Двоичная арифметика
Двоичная арифметика Задачи на дроби
Задачи на дроби Числа и точки на прямой. 5 класс
Числа и точки на прямой. 5 класс Тригонометрический круг, определение синуса, косинуса, тангенса и котангенса
Тригонометрический круг, определение синуса, косинуса, тангенса и котангенса Осевая симметрия
Осевая симметрия Самостоятельная работа по теме Векторы
Самостоятельная работа по теме Векторы