Содержание
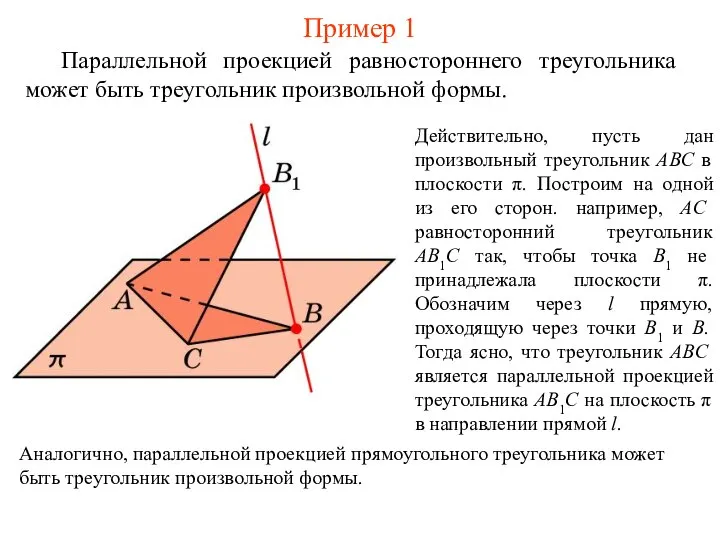
- 2. Пример 1 Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы. Действительно, пусть дан произвольный треугольник
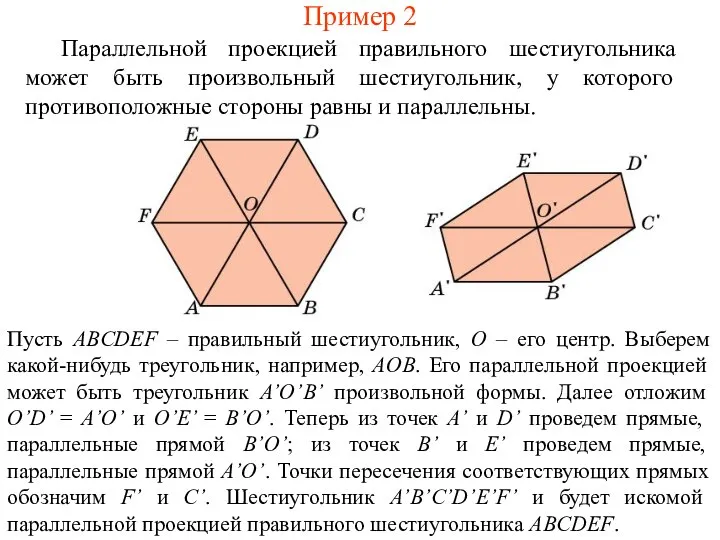
- 3. Пример 2 Параллельной проекцией правильного шестиугольника может быть произвольный шестиугольник, у которого противоположные стороны равны и
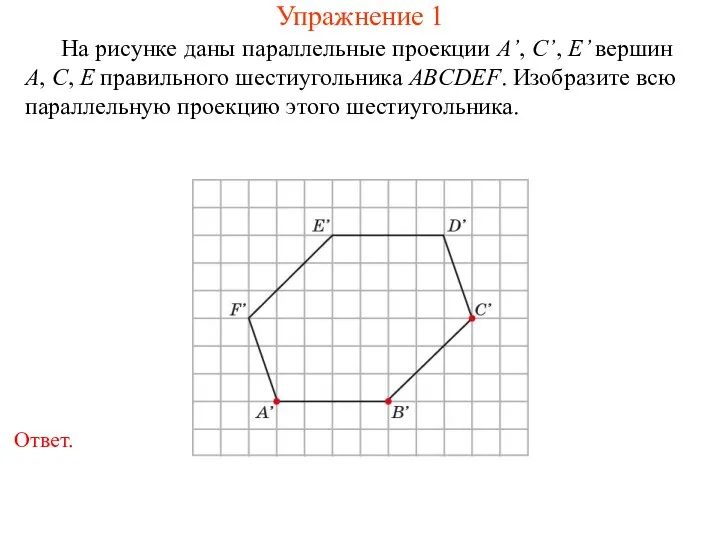
- 4. Упражнение 1 На рисунке даны параллельные проекции A’, C’, E’ вершин A, C, E правильного шестиугольника
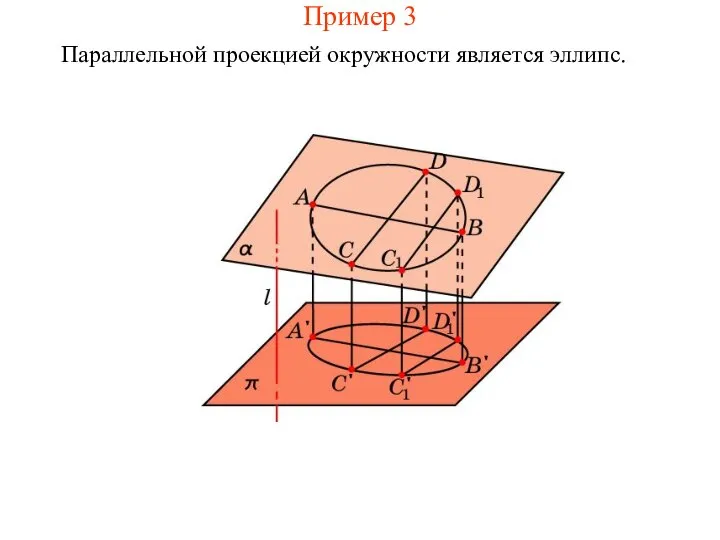
- 5. Пример 3 Параллельной проекцией окружности является эллипс.
- 6. Упражнение 3 Какие фигуры могут служить параллельными проекциями треугольника? Ответ: Треугольник или отрезок.
- 7. Упражнение 4 Может ли параллельной проекцией равностороннего треугольника быть: а) прямоугольный треугольник; б) равнобедренный треугольник; в)
- 8. Упражнение 5 Какой фигурой может быть параллельная проекция прямоугольника? Ответ: Параллелограммом или отрезком.
- 9. Упражнение 6 Может ли параллельной проекцией прямоугольника быть: а) квадрат; б) параллелограмм; в) ромб; г) трапеция?
- 10. Упражнение 7 Верно ли, что проекцией ромба, если он не проектируется в отрезок, будет ромб? Ответ:
- 11. Упражнение 8 Параллельной проекцией каких фигур может быть квадрат? Ответ: Параллелограммов.
- 12. Упражнение 9 В какую фигуру может проектироваться трапеция? Ответ: Трапецию или отрезок.
- 14. Скачать презентацию







 Прямая и плоскость в пространстве
Прямая и плоскость в пространстве Решение задач
Решение задач Простейшие геометрические уравнения
Простейшие геометрические уравнения Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников Обработка экспериментальных данных. Описательная статистика: основные понятия
Обработка экспериментальных данных. Описательная статистика: основные понятия Окружность и её элементы
Окружность и её элементы Формулы двойного угла
Формулы двойного угла Экскурсия в мир чисел
Экскурсия в мир чисел Параллельные прямые в пространстве
Параллельные прямые в пространстве Действительный анализ. Интеграл Римана и критерий Лебега
Действительный анализ. Интеграл Римана и критерий Лебега Сфера
Сфера Многогранники
Многогранники Определенный интеграл. Пример 2. Лекция
Определенный интеграл. Пример 2. Лекция Логарифмические уравнения (часть 2)
Логарифмические уравнения (часть 2) Правила комбинаторики. Практическое занятие
Правила комбинаторики. Практическое занятие Презентация на тему Теорема Фалеса
Презентация на тему Теорема Фалеса  Смежные углы
Смежные углы Занимательная математика
Занимательная математика Системы линейных уравнений
Системы линейных уравнений Применение интеграла в физике и геометрии
Применение интеграла в физике и геометрии Сумма углов в треугольнике
Сумма углов в треугольнике Логика и математическая логика. История логики. Алгебра высказываний
Логика и математическая логика. История логики. Алгебра высказываний Сложение и вычитание дробей
Сложение и вычитание дробей Правильные многогранники
Правильные многогранники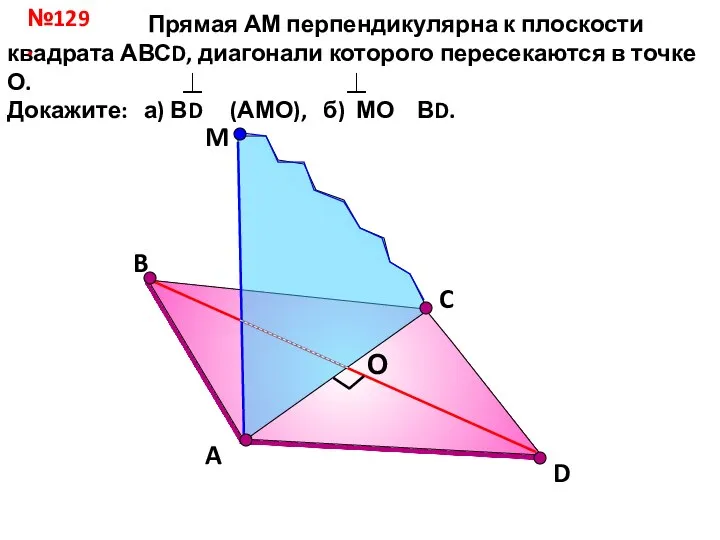 Прямая АМ перпендикулярна к плоскости квадрата АВСD. урок 29
Прямая АМ перпендикулярна к плоскости квадрата АВСD. урок 29 Сложение вида +2, +3
Сложение вида +2, +3 Презентация по математике "Основы концепции “глубинного анализа текстов" -
Презентация по математике "Основы концепции “глубинного анализа текстов" -  Учимся писать цифры
Учимся писать цифры