= 10
2. Решите уравнение в целых числах 4х2 - 2у2 = 13
3. В Мексике экологи добились принятия закона, по которому каждый автомобиль хотя бы один день в неделю не должен ездить (владелец сообщает полиции номер автомобиля и «выходной» день недели этого автомобиля). В некоторой семье все взрослые желают ездить ежедневно (каждый — по своим делам!). Сколько автомобилей (как минимум) должно быть в семье, если взрослых в ней а) 5 человек? б) 8 человек?
4. В старших классах школы учатся 300 учеников, которые изучают иностранные языки (каждый ученик изучает хотя бы один иностранный язык). Найдите количество учеников, которые изучают все иностранные языки в каждом из следующих случаев:
А) английский изучают 240 человек, немецкий – 84
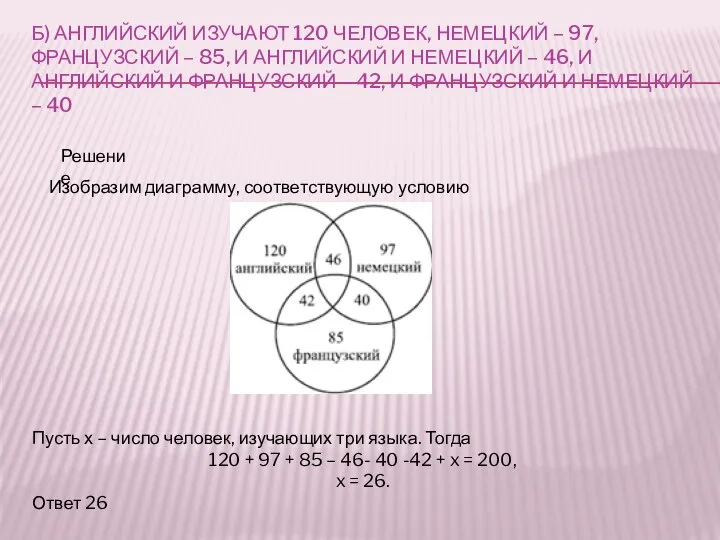
Б) английский изучают 240 человек, немецкий – 84, французский – 63, и английский и немецкий – 57, и английский и французский – 24, и французский и немецкий – 40
В) английский изучают 120 человек, немецкий 60, французский 100. И для каждой пары языков найдется не более 20 человек, изучающих оба языка.








 Гомотетия. Гомотетичные фигуры
Гомотетия. Гомотетичные фигуры Презентация на тему СВОЙСТВА АРИФМЕТИЧЕСКОГО КОРНЯ
Презентация на тему СВОЙСТВА АРИФМЕТИЧЕСКОГО КОРНЯ  Углы между прямыми и плоскостями (координатный метод), 11 класс
Углы между прямыми и плоскостями (координатный метод), 11 класс reshenie-trigonometricheskih-uravneniy-i-sposoby-otbora-korney-na-zadannom-promezhutke
reshenie-trigonometricheskih-uravneniy-i-sposoby-otbora-korney-na-zadannom-promezhutke Матрицы. Действия над матрицами
Матрицы. Действия над матрицами Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Призма и ее виды. Чертеж призмы
Призма и ее виды. Чертеж призмы Задача на спрос и предложение
Задача на спрос и предложение Круг, окружность, длина окружности. 6 класс
Круг, окружность, длина окружности. 6 класс Исследование на принадлежность классам функцию. Практическая работа
Исследование на принадлежность классам функцию. Практическая работа Раскраска графов. Лекция 07
Раскраска графов. Лекция 07 Probability Distributions
Probability Distributions Математические ребусы
Математические ребусы Cхема (метод) Горнера. Способ деления многочлена
Cхема (метод) Горнера. Способ деления многочлена Окружность Аполлония
Окружность Аполлония Угол между векторами
Угол между векторами Что такое математика?
Что такое математика? Арифметические действия
Арифметические действия Теорема. Франсуа Виет (1540-1603)
Теорема. Франсуа Виет (1540-1603) Квадратные уравнения. Основные понятия
Квадратные уравнения. Основные понятия Метрология, основные понятия
Метрология, основные понятия Урок-КВН
Урок-КВН Умножение для ленивых? 5 класс
Умножение для ленивых? 5 класс Метрическая система мер
Метрическая система мер Основы анализа данных. Метод наименьших квадратов. (Лекция 6)
Основы анализа данных. Метод наименьших квадратов. (Лекция 6)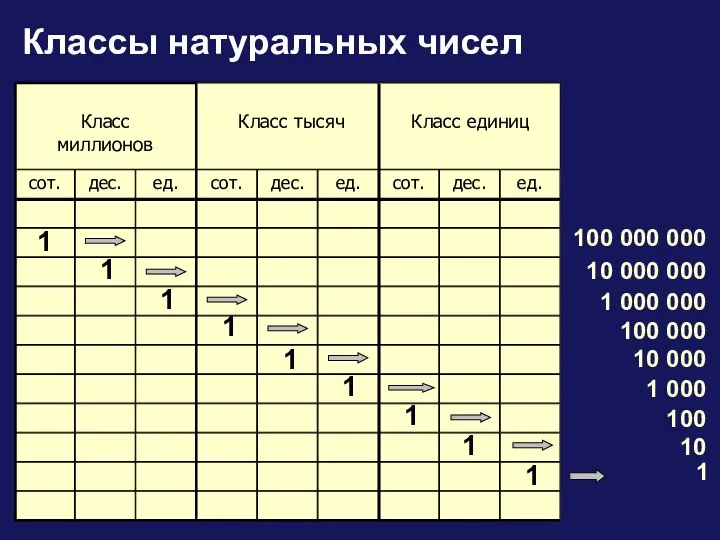 Классы натуральных чисел
Классы натуральных чисел Число и цифра 8
Число и цифра 8 Правильные многоугольники
Правильные многоугольники