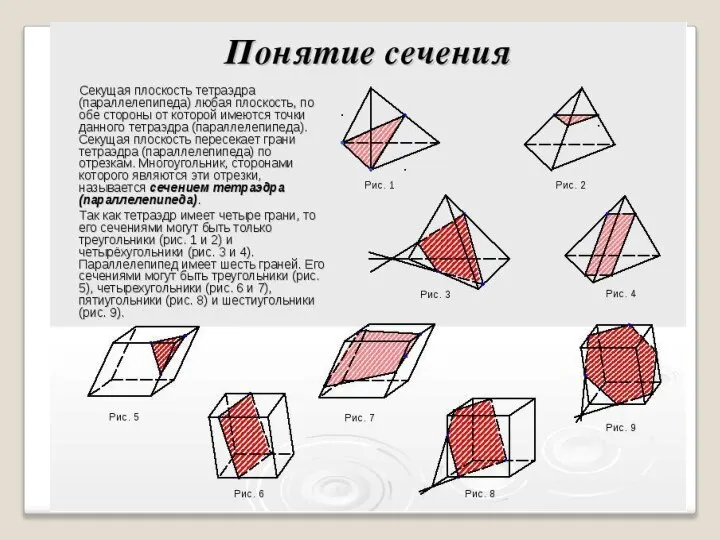
Содержание
- 3. Содержанием работы является построение сечений по точкам, заданным на рёбрах многогранников: 2. Пирамиды 3. Призмы 1.
- 4. А В С D A1 B1 C1 D1 Дан куб A B C D A1 B1
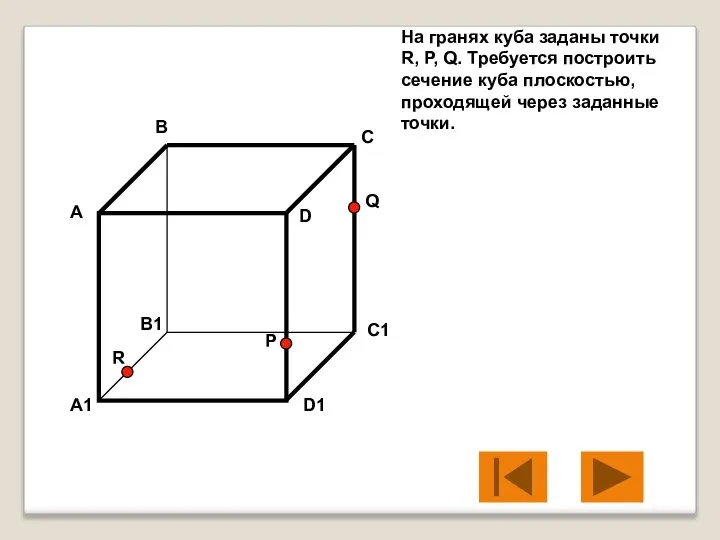
- 5. На гранях куба заданы точки R, P, Q. Требуется построить сечение куба плоскостью, проходящей через заданные
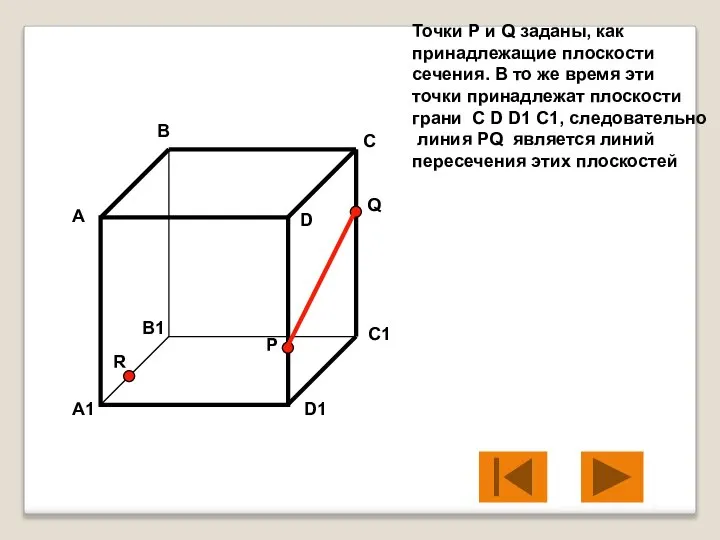
- 6. Точки Р и Q заданы, как принадлежащие плоскости сечения. В то же время эти точки принадлежат
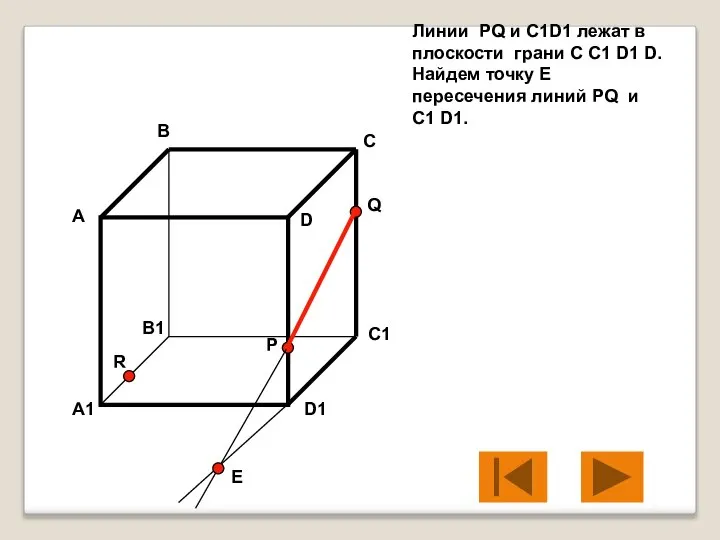
- 7. Линии PQ и C1D1 лежат в плоскости грани C C1 D1 D. Найдем точку Е пересечения
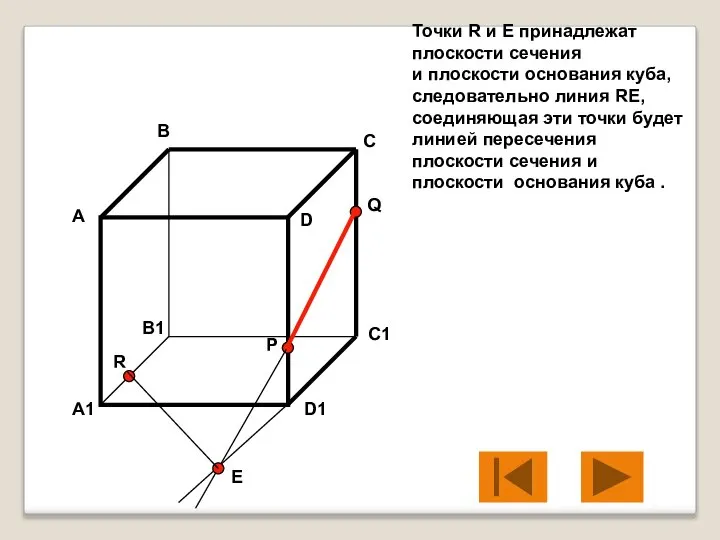
- 8. Точки R и E принадлежат плоскости сечения и плоскости основания куба, следовательно линия RE, соединяющая эти
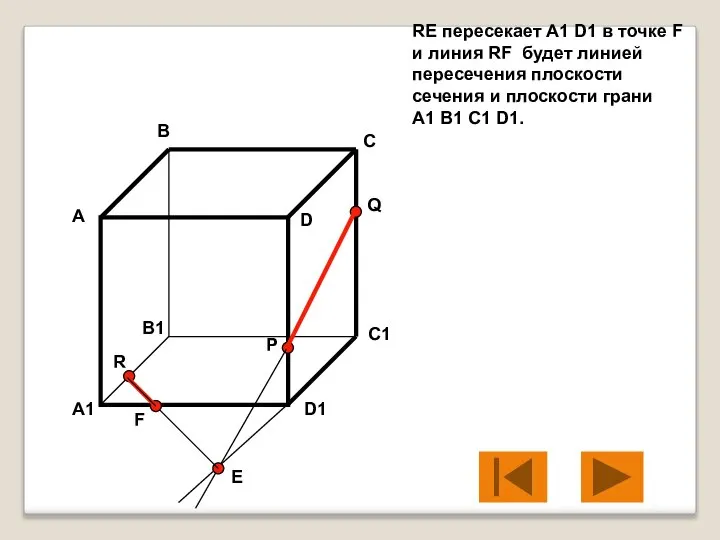
- 9. RE пересекает A1 D1 в точке F и линия RF будет линией пересечения плоскости сечения и
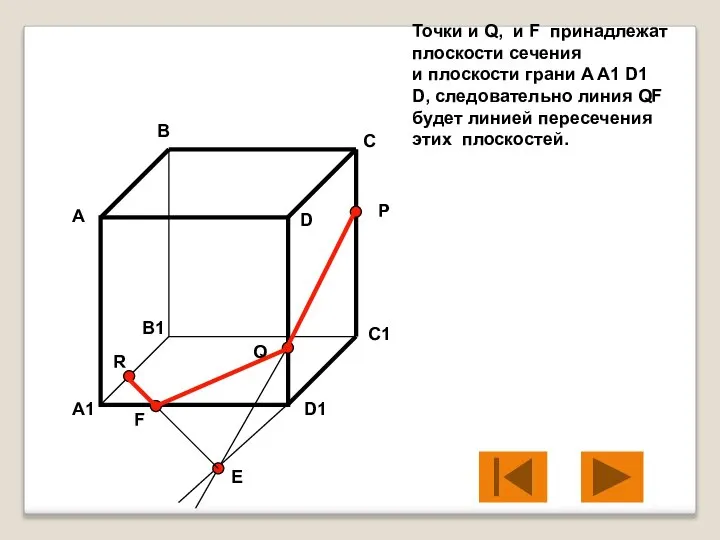
- 10. Точки и Q, и F принадлежат плоскости сечения и плоскости грани A A1 D1 D, следовательно
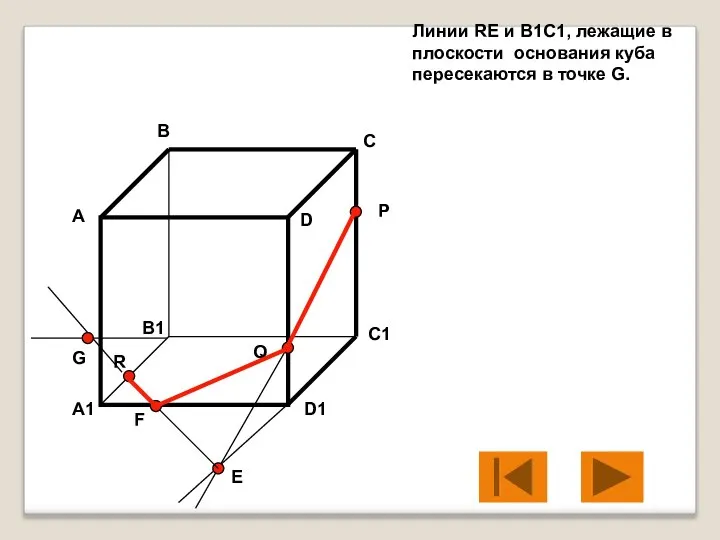
- 11. Линии RE и B1C1, лежащие в плоскости основания куба пересекаются в точке G. А В С
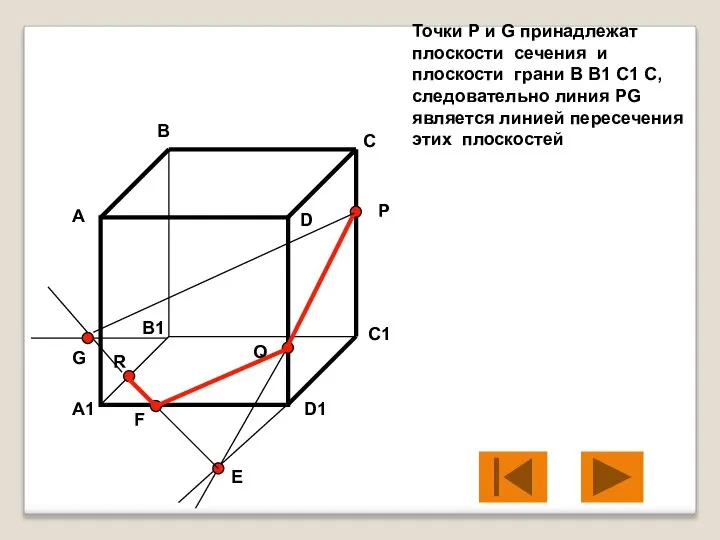
- 12. Точки P и G принадлежат плоскости сечения и плоскости грани B B1 C1 C, следовательно линия
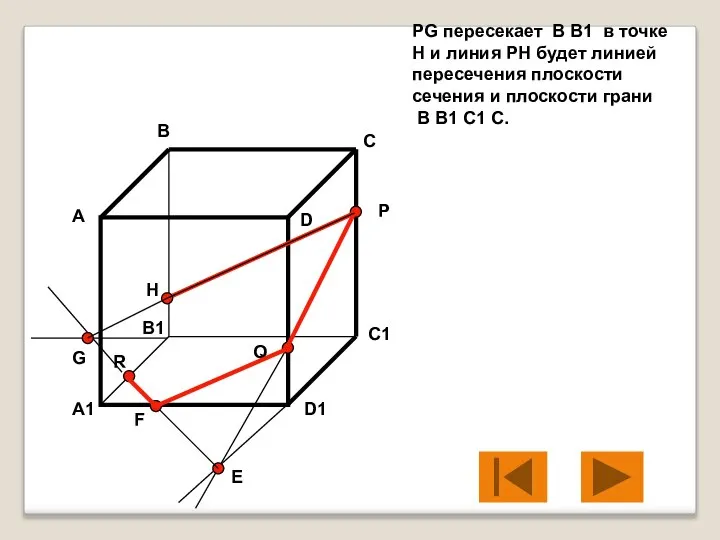
- 13. PG пересекает B B1 в точке H и линия PH будет линией пересечения плоскости сечения и
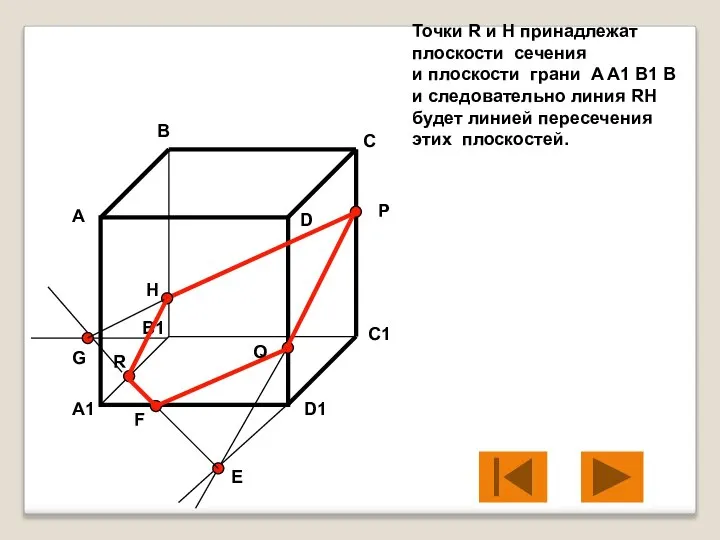
- 14. Точки R и H принадлежат плоскости сечения и плоскости грани A A1 B1 B и следовательно
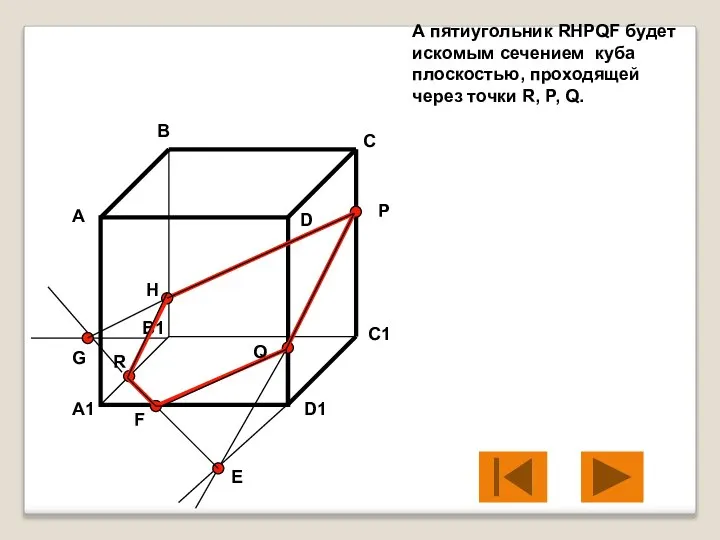
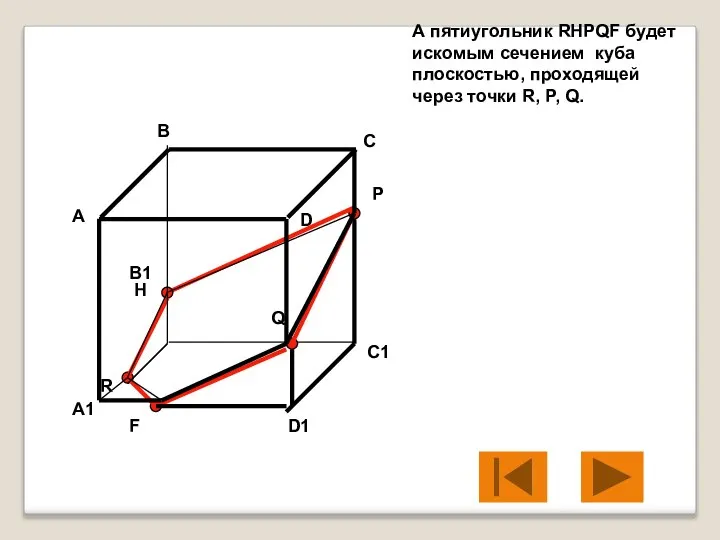
- 15. А пятиугольник RHPQF будет искомым сечением куба плоскостью, проходящей через точки R, P, Q. А В
- 16. А пятиугольник RHPQF будет искомым сечением куба плоскостью, проходящей через точки R, P, Q. А В
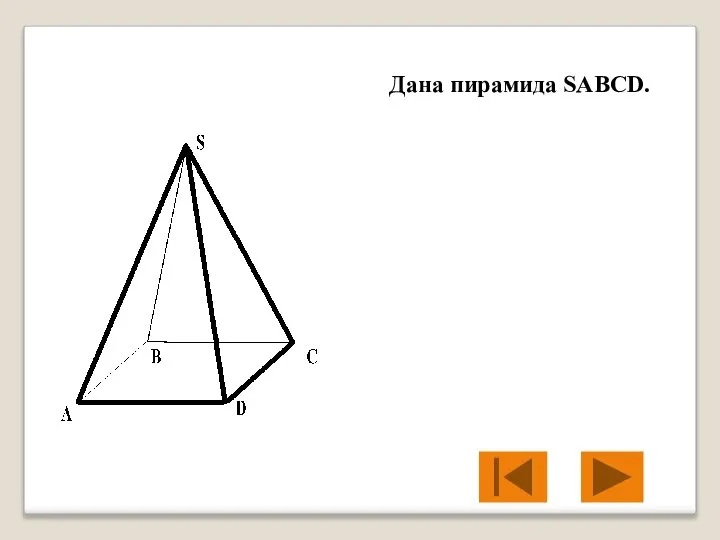
- 17. Дана пирамида SABCD.
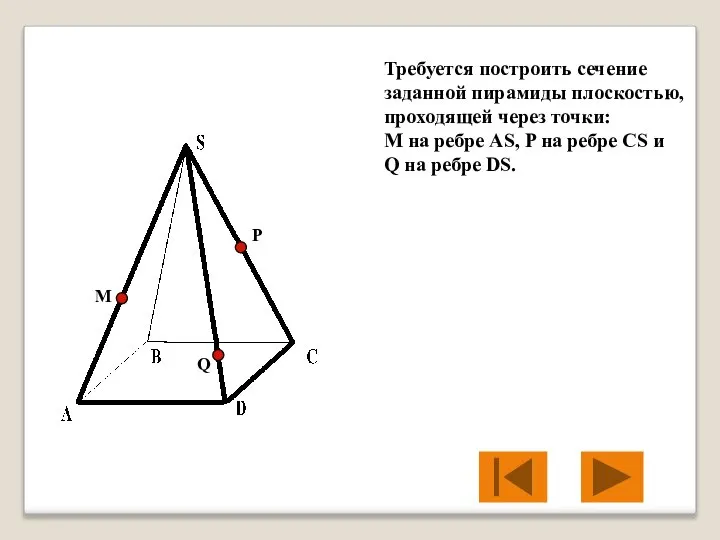
- 18. Требуется построить сечение заданной пирамиды плоскостью, проходящей через точки: М на ребре AS, P на ребре
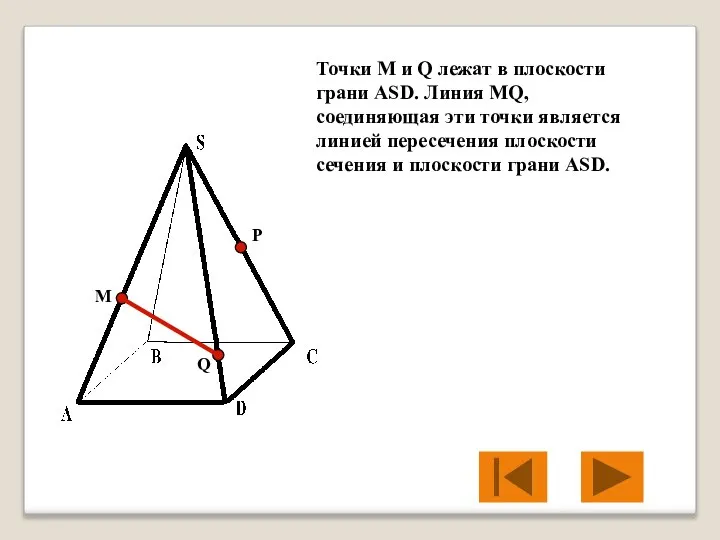
- 19. M P Q Точки M и Q лежат в плоскости грани АSD. Линия МQ, соединяющая эти
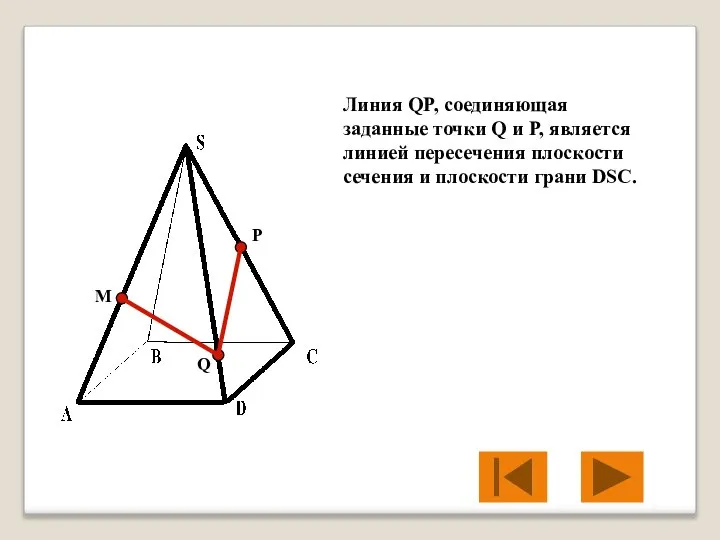
- 20. M P Q Линия QP, соединяющая заданные точки Q и P, является линией пересечения плоскости сечения
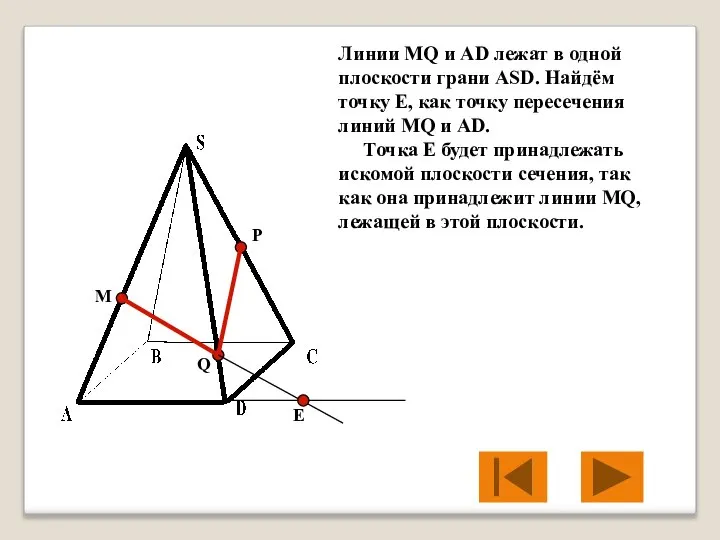
- 21. M P Q Линии MQ и AD лежат в одной плоскости грани ASD. Найдём точку Е,
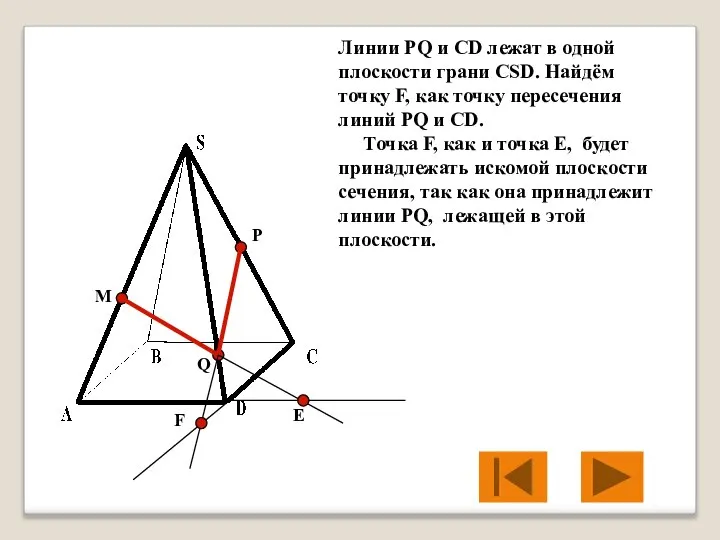
- 22. M P Q Е Линии PQ и CD лежат в одной плоскости грани CSD. Найдём точку
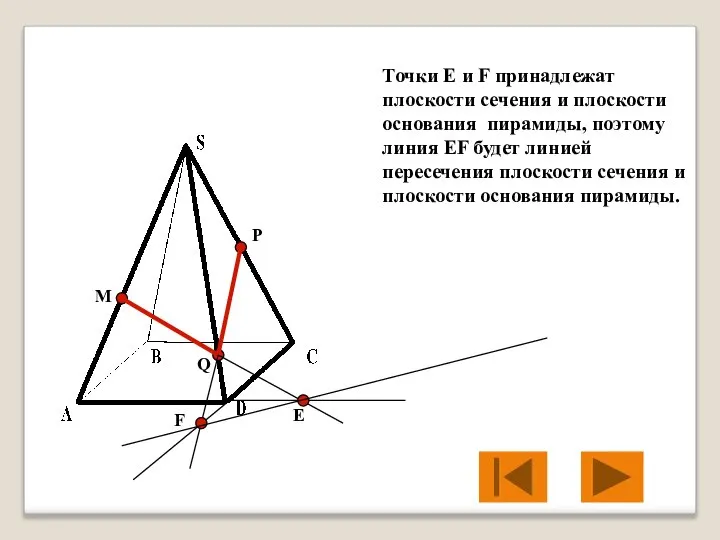
- 23. M P Q Е F Точки Е и F принадлежат плоскости сечения и плоскости основания пирамиды,
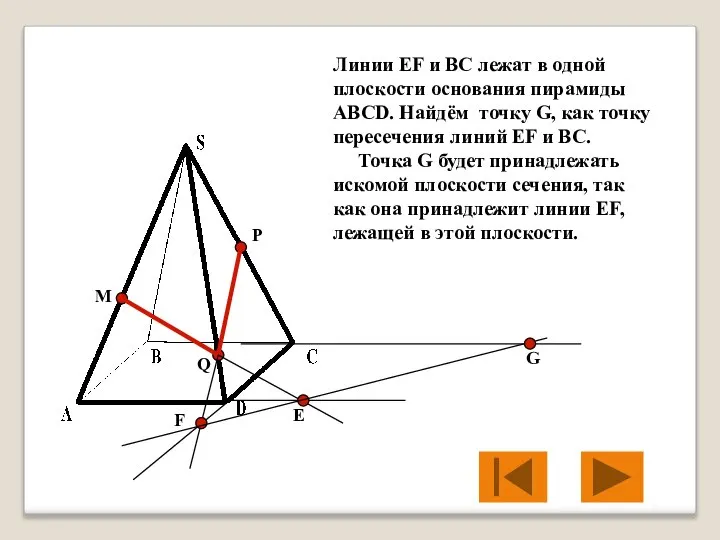
- 24. M P Q Е F Линии EF и BC лежат в одной плоскости основания пирамиды ABCD.
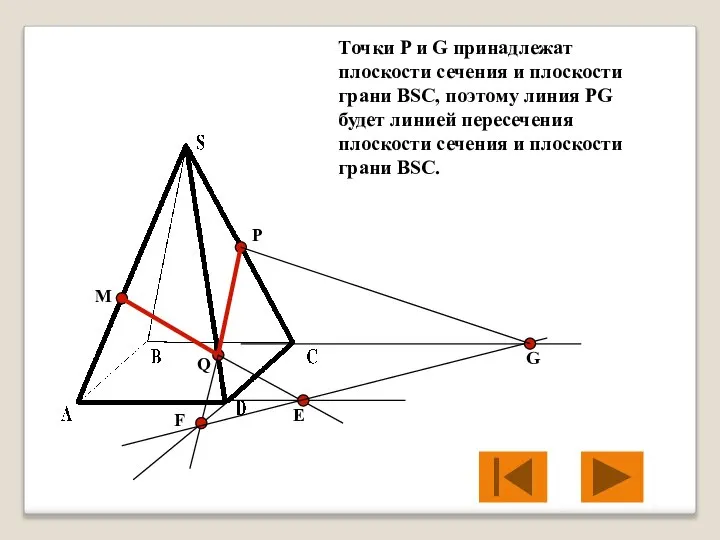
- 25. M P Q Е F G Точки P и G принадлежат плоскости сечения и плоскости грани
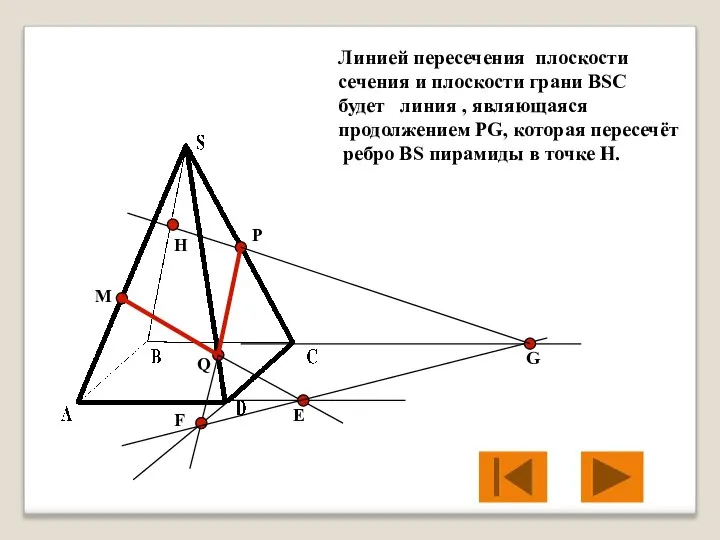
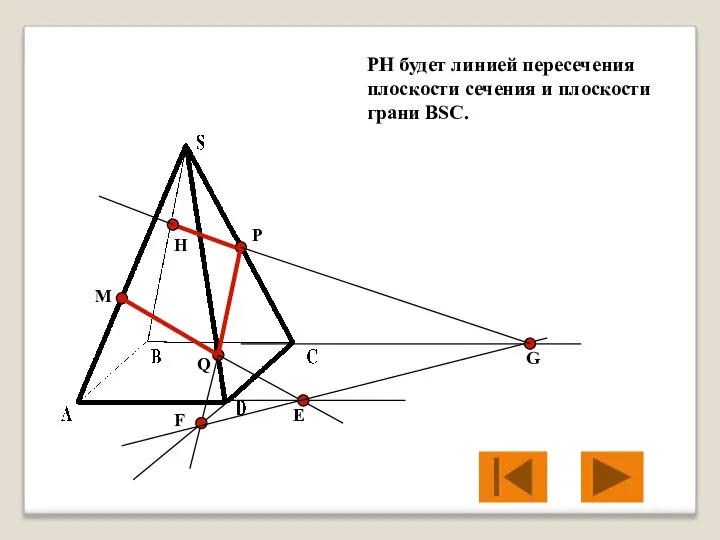
- 26. M P Q Е F G Линией пересечения плоскости сечения и плоскости грани BSC будет линия
- 27. M P Q Е F G H PH будет линией пересечения плоскости сечения и плоскости грани
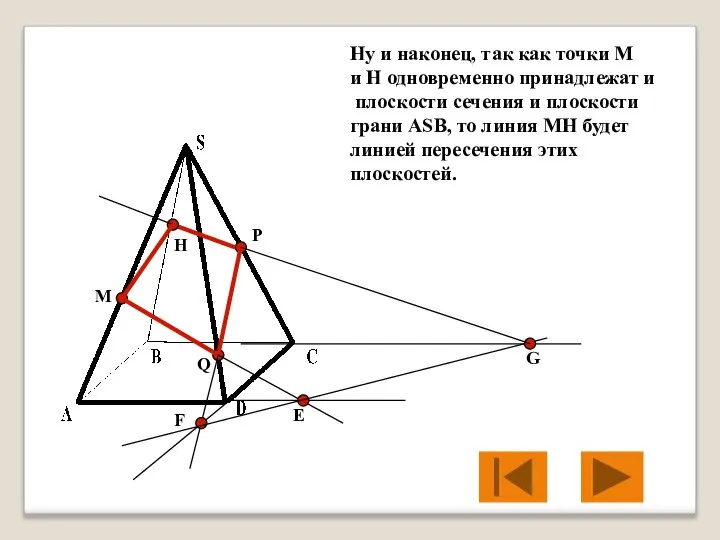
- 28. M P Q Е F G H Ну и наконец, так как точки M и H
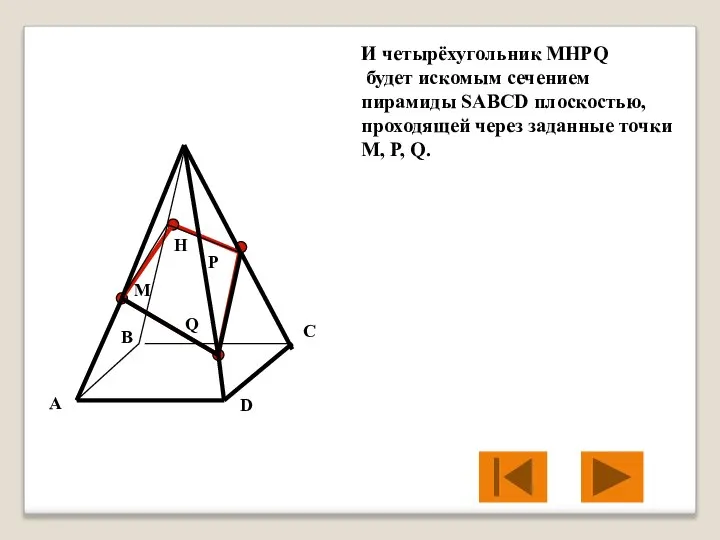
- 29. M P Q H И четырёхугольник MHPQ будет искомым сечением пирамиды SABCD плоскостью, проходящей через заданные
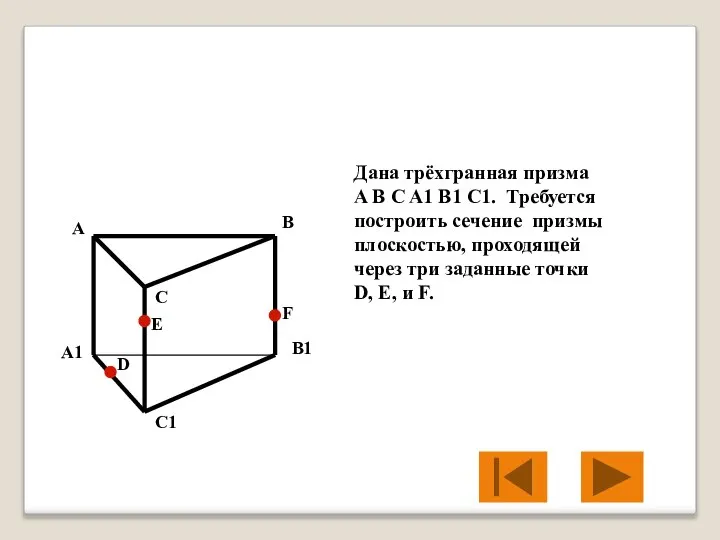
- 30. Дана трёхгранная призма A B C A1 B1 C1. Требуется построить сечение призмы плоскостью, проходящей через
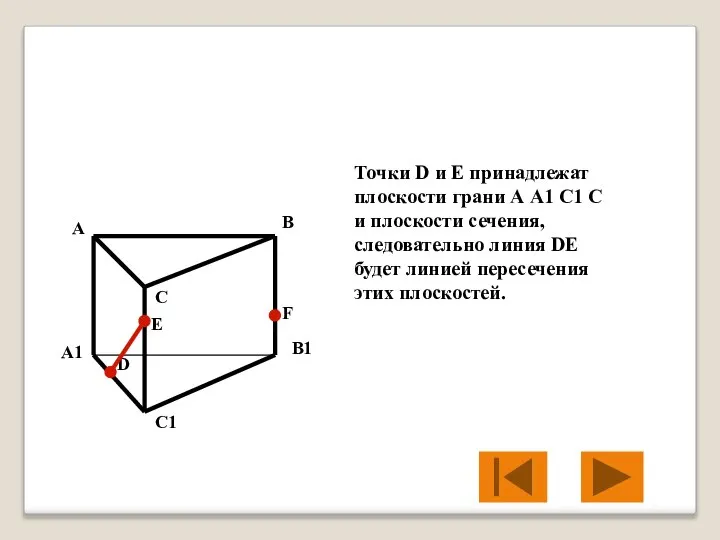
- 31. Точки D и E принадлежат плоскости грани А А1 С1 С и плоскости сечения, следовательно линия
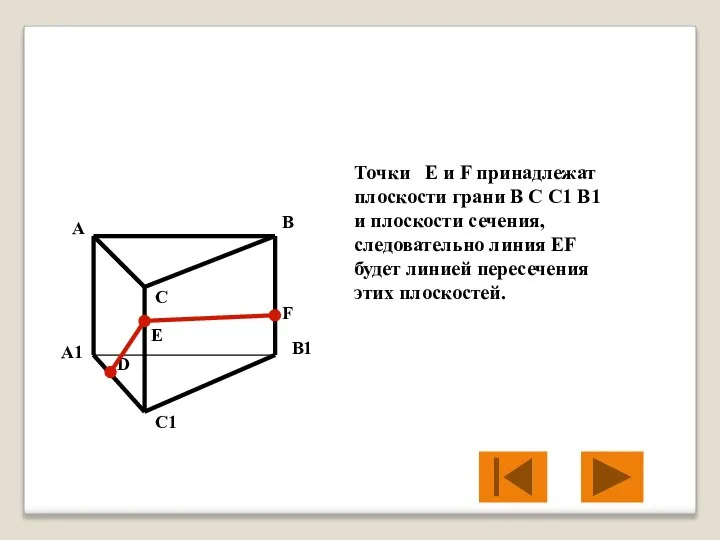
- 32. Точки E и F принадлежат плоскости грани B C C1 B1 и плоскости сечения, следовательно линия
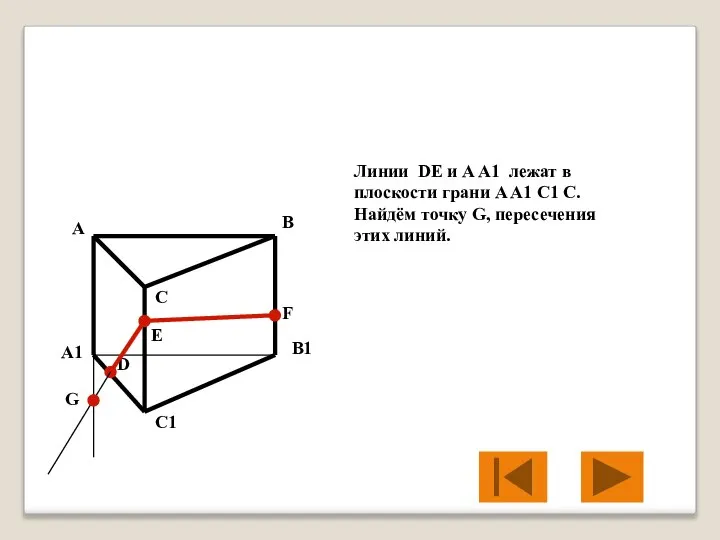
- 33. Линии DE и A A1 лежат в плоскости грани A A1 C1 C. Найдём точку G,
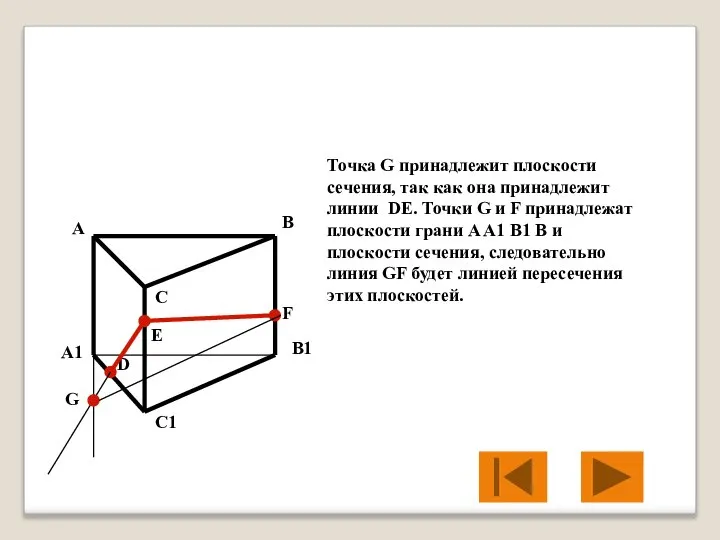
- 34. Точка G принадлежит плоскости сечения, так как она принадлежит линии DE. Точки G и F принадлежат
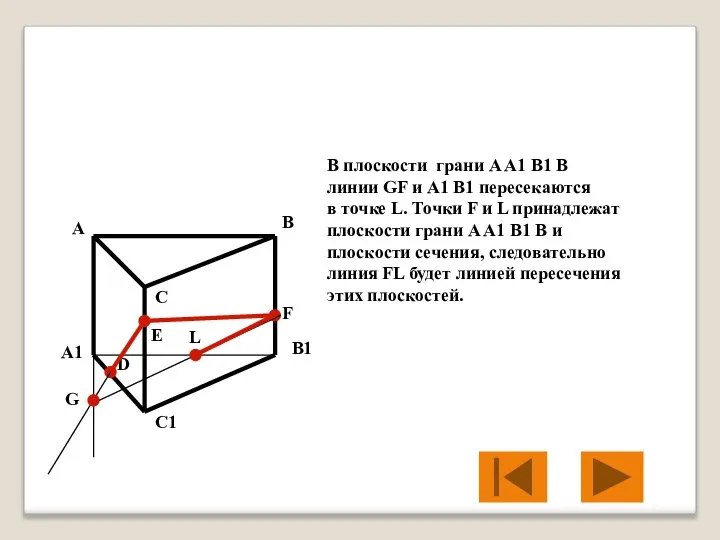
- 35. В плоскости грани A A1 B1 B линии GF и A1 B1 пересекаются в точке L.
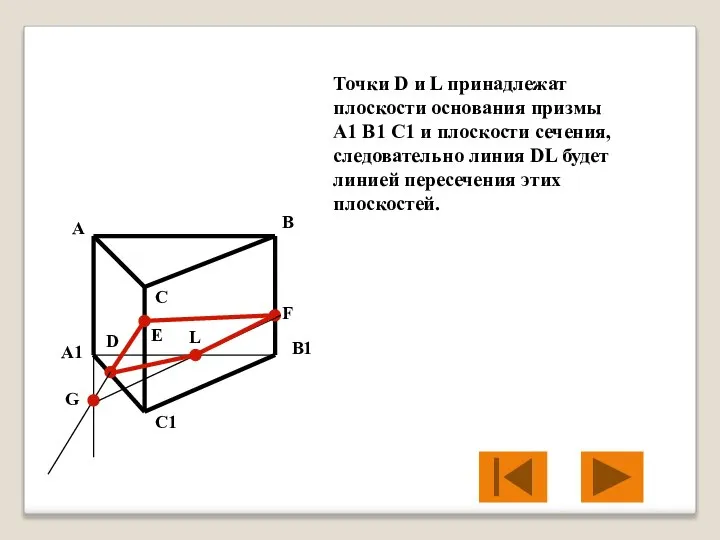
- 36. Точки D и L принадлежат плоскости основания призмы A1 B1 C1 и плоскости сечения, следовательно линия
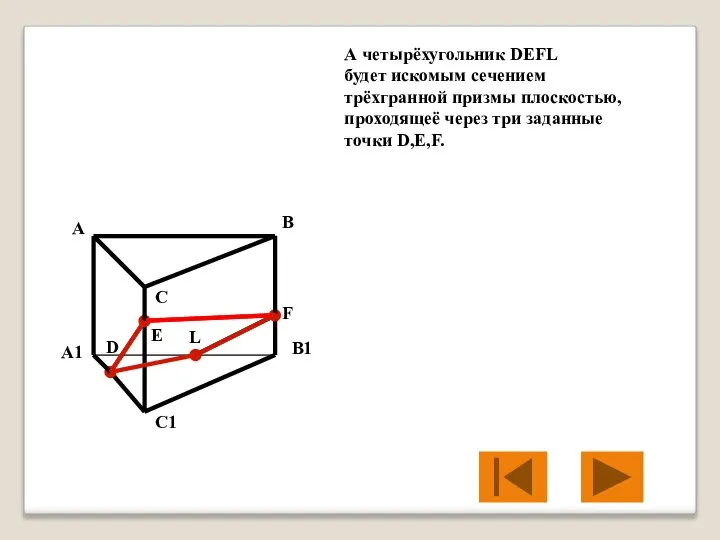
- 37. А четырёхугольник DEFL будет искомым сечением трёхгранной призмы плоскостью, проходящеё через три заданные точки D,E,F. A
- 39. Скачать презентацию

 Интегральное исчисление. Функция. Предел функции
Интегральное исчисление. Функция. Предел функции Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов
Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов Презентация на тему Смежные углы
Презентация на тему Смежные углы  Множители и произведение
Множители и произведение Аппроксимация функций. Метод Лагранжа
Аппроксимация функций. Метод Лагранжа Основы тригонометрии. Радианная мера угла. Вращательное движение точки вокруг начла координат
Основы тригонометрии. Радианная мера угла. Вращательное движение точки вокруг начла координат Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Четырехзначные числа (3 класс)
Четырехзначные числа (3 класс) Помоги Незнайке выполнить задание от Знайки
Помоги Незнайке выполнить задание от Знайки Статистический образ мышления. Научная публикация. (Лекция 3)
Статистический образ мышления. Научная публикация. (Лекция 3) Числовые головоломки
Числовые головоломки Объем конуса
Объем конуса Клуб весёлых и находчивых. Турнир любителей математики
Клуб весёлых и находчивых. Турнир любителей математики Решение задач по теме: Прямоугольник. Ромб. Квадрат
Решение задач по теме: Прямоугольник. Ромб. Квадрат Булева алгебра
Булева алгебра Правильные многогранники
Правильные многогранники Несобственные интегралы первого рода
Несобственные интегралы первого рода Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Эквивалентные преобразования матриц
Эквивалентные преобразования матриц Таблица значений синуса и тангенса для углов
Таблица значений синуса и тангенса для углов Решение задач
Решение задач Ariile figurilor geometrice plane
Ariile figurilor geometrice plane Презентация на тему ИЗМЕРЕНИЕ ОТРЕЗКОВ
Презентация на тему ИЗМЕРЕНИЕ ОТРЕЗКОВ  Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника По следам теоремы Пифагора
По следам теоремы Пифагора Функция
Функция Многогранники + точки. Лекция 5
Многогранники + точки. Лекция 5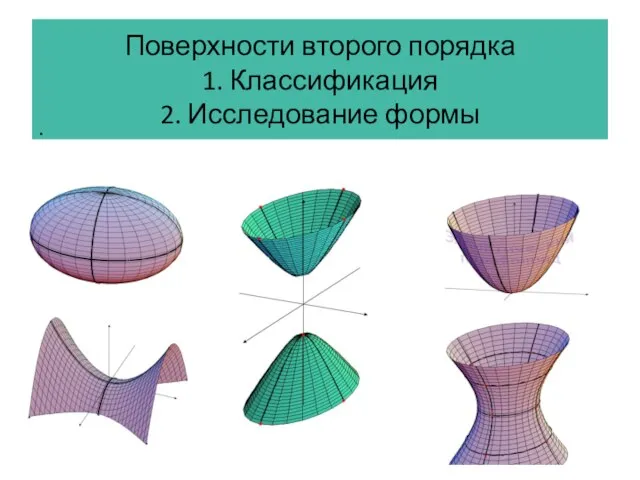 Поверхности второго порядка
Поверхности второго порядка