Школа олимпийского резерва. (задача)

Создадим 3 массива, согласно году рождения
Отсортируем каждый из массивов по убыванию баллов
Переберем значения M94, M95, M96:
проверяем M94 + M95 + M96 = M и
T94[M94] > T95[M95], T95[M95] > T96[M96]
T94 Т95 Т96 Ищем минимум
М96 Сложность O(N3)
M94 M95 25 баллов

Заметим, что если мы фиксировали значения M94 и M95, то
M96 = A + B + C – (M94 + M95), так как
A + B + C = M94 + M95 + M96 = M по условию
Остается проверить, что полученное значение M96 удовлетворяет условиям
1 ≤ M96 ≤ N96,
T94[M94] > T95[M95], T95[M95] > T96[M96]
и найти среди таких троек ту,
на которой достигается минимум функции
Сложность O(N2) 50 баллов

Оптимальное решение
T94 Т95 Т96
М96
M94 M95
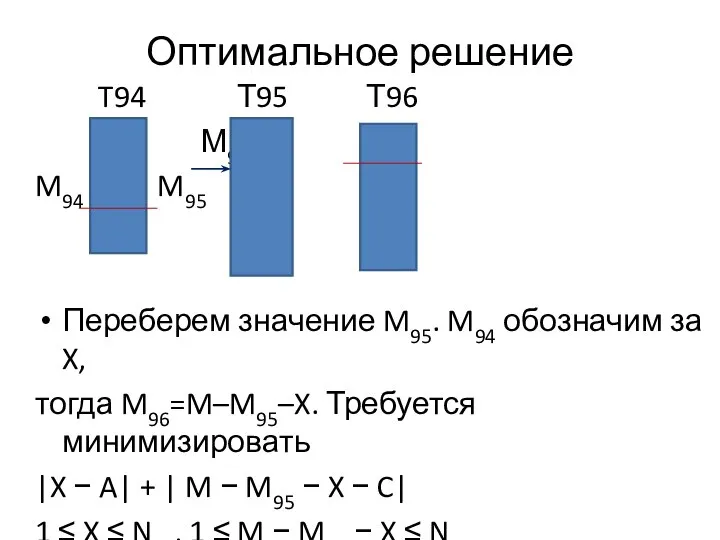
Переберем значение M95. M94 обозначим за X,
тогда M96=M–M95–X. Требуется минимизировать
|X − A| + | M − M95 − X − C|
1 ≤ X ≤ N94, 1 ≤ M − M95 − X ≤ N96

Допустимые значения X
T94 Т95 Т96
m96
m94 M95
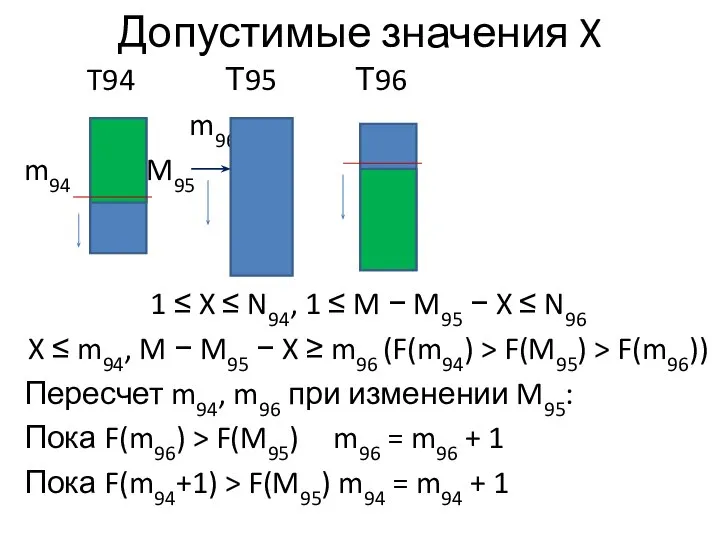
1 ≤ X ≤ N94, 1 ≤ M − M95 − X ≤ N96
X ≤ m94, M − M95 − X ≥ m96 (F(m94) > F(M95) > F(m96))
Пересчет m94, m96 при изменении M95:
Пока F(m96) > F(M95) m96 = m96 + 1
Пока F(m94+1) > F(M95) m94 = m94 + 1