- Главная
- Математика
- Симплексный метод планирования. Лекция 6

Содержание
- 2. Метод симплексного планирования позволяет без предварительного изучения влияния факторов найти область оптимума. В этом методе не
- 3. Рис. 1. Схема движения к оптимальной области симплексным методом По итогам проведения опытов 1, 2 и
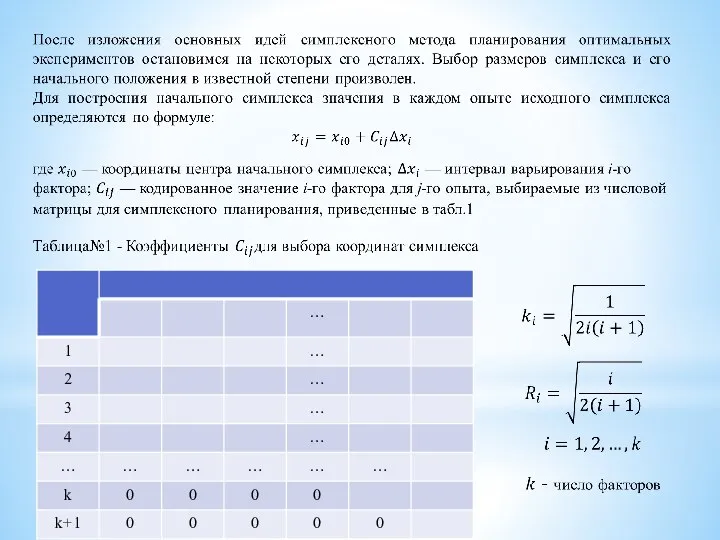
- 5. Симплекс, рассчитанный по этим формулам, представлен на рис. 2 Рис. 2. Схема построения начального симплекса
- 6. Так, если x10=0 и x20=0, а∆x1=∆x2=1, то координаты опытов будут равны (см. рис.3): опыт 1 (0,5;0,289),
- 7. Известны следующие критерии окончания процесса последовательного отражения наихудших вершин и постановки очередных опытов в новых вершинах:
- 11. Скачать презентацию
Слайд 2Метод симплексного планирования позволяет без предварительного изучения влияния факторов найти область оптимума.
Метод симплексного планирования позволяет без предварительного изучения влияния факторов найти область оптимума.

Симплекс — это простейший выпуклый многогранник, образованный k+1 вершинами в k-мерном пространстве, которые соединены между собой прямыми линиями. При этом координаты вершин симплекса являются значениями факторов в отдельных опытах. Так, например, в двухфакторном пространстве (на плоскости) k=2 симплекс — любой треугольник, в трехфакторном (трехмерном) k=3 пространстве — тетраэдр и т.д.
Симплекс называется правильным или регулярным, если все расстояния между образующими его вершинами равны (равносторонний треугольник, правильный тетраэдр и др.).
После построения исходного симплекса и проведения опытов при значениях факторов, соответствующих координатам его вершин, анализируют результаты и выбирают вершину симплекса, в которой получено наименьшее (наихудшее) значение функции отклика. Для движения к оптимуму необходимо поставить опыт в новой точке, являющейся зеркальным отображением точки с наихудшим (минимальным) результатом относительно противоположной грани симплекса.
Метод симплексного планирования
Слайд 3Рис. 1. Схема движения к оптимальной
области симплексным методом
По итогам проведения опытов
Рис. 1. Схема движения к оптимальной
области симплексным методом
По итогам проведения опытов

Следует заметить, что хотя этот путь и зигзагообразен, общее число опытов, необходимых для достижения области оптимума, может быть небольшим за счет того, что проводить k+1 опыт приходится лишь в начале, а в дальнейшем каждый шаг сопровождается проведением только одного дополнительного опыта, условия которого выбираются на основе предшествующих результатов.
Слайд 5
Симплекс, рассчитанный по этим формулам, представлен на рис. 2
Рис. 2. Схема построения
Симплекс, рассчитанный по этим формулам, представлен на рис. 2
Рис. 2. Схема построения

Слайд 6Так, если x10=0 и x20=0, а∆x1=∆x2=1, то координаты опытов будут равны (см.
Так, если x10=0 и x20=0, а∆x1=∆x2=1, то координаты опытов будут равны (см.

опыт 1 (0,5;0,289),
опыт 2 (-0,5; 0,289)
опыт 3 (0;-0,577),
что соответствует координатам вершин равностороннего треугольника с длиной стороны,
равной 1.
Начало координат в этом случае находится в точке пересечения медиан (биссектрис).
Рис. 3. Координаты вершин симплекса
Слайд 7
Известны следующие критерии окончания процесса последовательного отражения наихудших вершин и постановки очередных
Известны следующие критерии окончания процесса последовательного отражения наихудших вершин и постановки очередных

2. Отражение любой из вершин симплекса после однократного качания приводит к его возврату в прежнее положение. При этом есть основания утверждать "накрытие" симплексом точки оптимума.
3. Циклическое движение симплекса вокруг одной из его вершин на протяжении более чем нескольких шагов. Подобная ситуация имеет место, когда искомый оптимум располагается внутри области, охватываемой циркулирующим симплексом.


 Планиметрия. Стереометрия
Планиметрия. Стереометрия Правильные многоугольники
Правильные многоугольники Критерий углового преобразования Фишера
Критерий углового преобразования Фишера Урок математики в 1 классе
Урок математики в 1 классе Бином Ньютона. Треугольник Паскаля
Бином Ньютона. Треугольник Паскаля Решение квадратного уравнения общего вида
Решение квадратного уравнения общего вида Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс
Степень с натуральным показателем. Применение свойств к построению графиков степенных функций. 7 класс Итоговый тест по алгебре для 7 класса
Итоговый тест по алгебре для 7 класса Уравнения математической физики
Уравнения математической физики Интегральные уравнения
Интегральные уравнения Критерий Манна-Уитни
Критерий Манна-Уитни Ребусы от тётушки Совы
Ребусы от тётушки Совы Уравнения – это ключ, открывающий все математические сезамы. С.Коваль
Уравнения – это ключ, открывающий все математические сезамы. С.Коваль Соединения с повторениями
Соединения с повторениями Точечное оценивание параметров распределений случайных величин
Точечное оценивание параметров распределений случайных величин Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  формулы сокрощенного умножения
формулы сокрощенного умножения Перпендикуляр и наклонные. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Тест
Перпендикуляр и наклонные. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Тест Упрощение выражений. Тест
Упрощение выражений. Тест Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат
Обобщающий урок по теме: параллелограм, прямоугольник, ромб, квадрат В мире цифр. Дидактическое пособие
В мире цифр. Дидактическое пособие Состав чисел первого десятка
Состав чисел первого десятка Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость
Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого Тригонометрические уравнения
Тригонометрические уравнения Правильные многоугольники
Правильные многоугольники Презентация на тему ГИА 2013. Модуль алгебра №6
Презентация на тему ГИА 2013. Модуль алгебра №6  Сложение, вычитание, умножение,
Сложение, вычитание, умножение,