Содержание
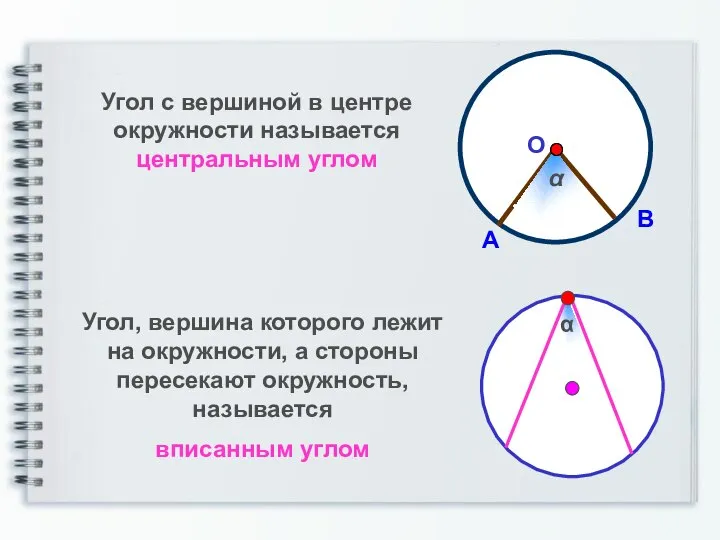
- 2. Угол с вершиной в центре окружности называется центральным углом Угол, вершина которого лежит на окружности, а
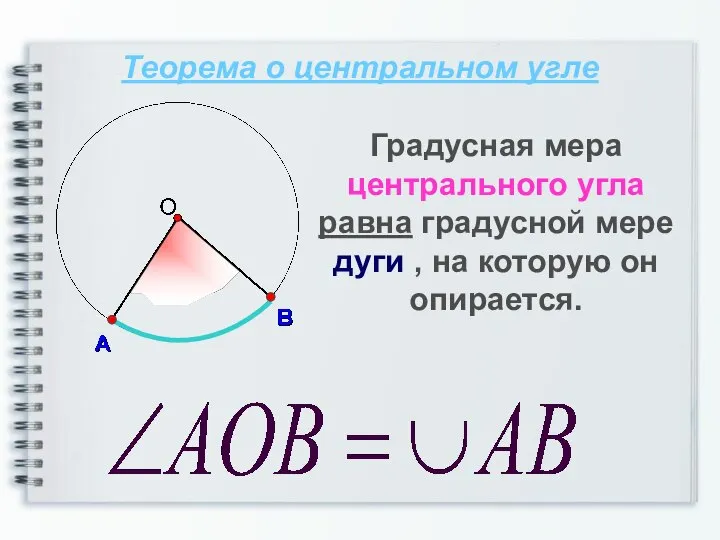
- 3. Теорема о центральном угле Градусная мера центрального угла равна градусной мере дуги , на которую он
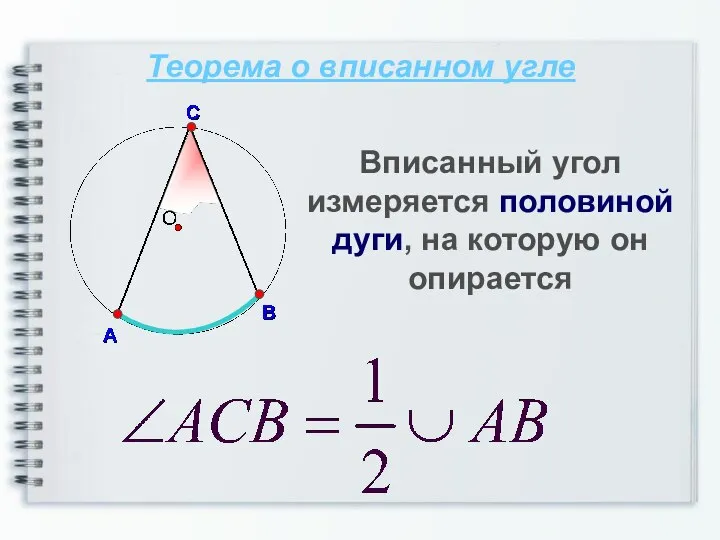
- 4. Теорема о вписанном угле Вписанный угол измеряется половиной дуги, на которую он опирается
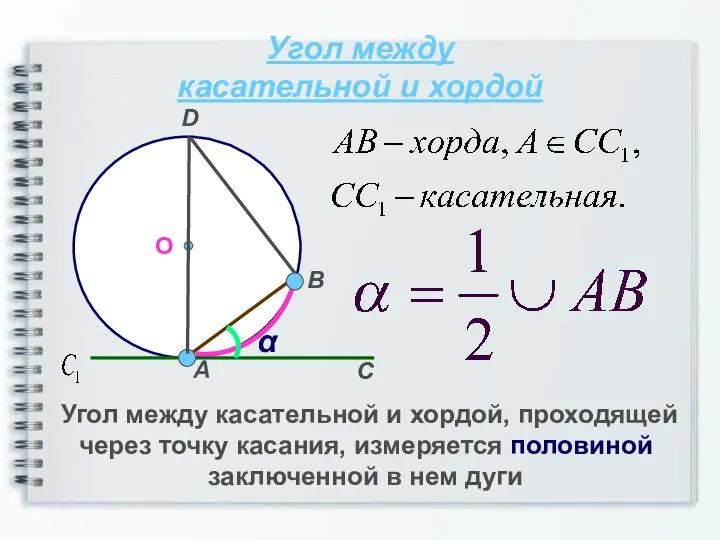
- 5. Угол между касательной и хордой О α Угол между касательной и хордой, проходящей через точку касания,
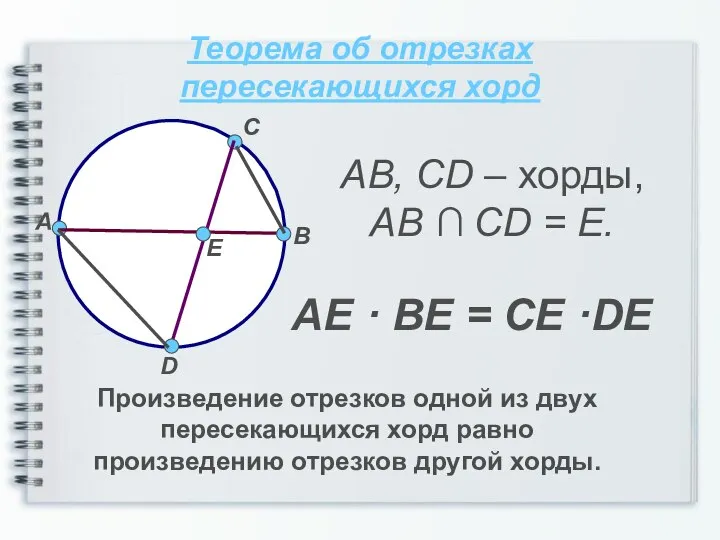
- 6. Теорема об отрезках пересекающихся хорд Произведение отрезков одной из двух пересекающихся хорд равно произведению отрезков другой
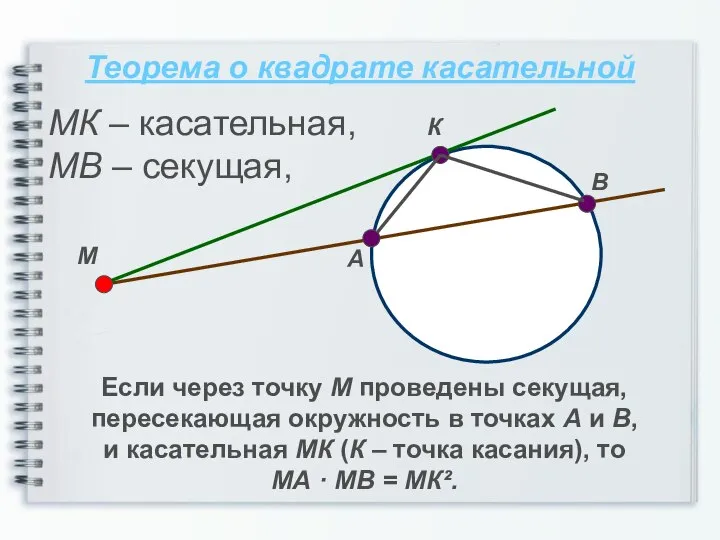
- 7. Теорема о квадрате касательной Если через точку М проведены секущая, пересекающая окружность в точках А и
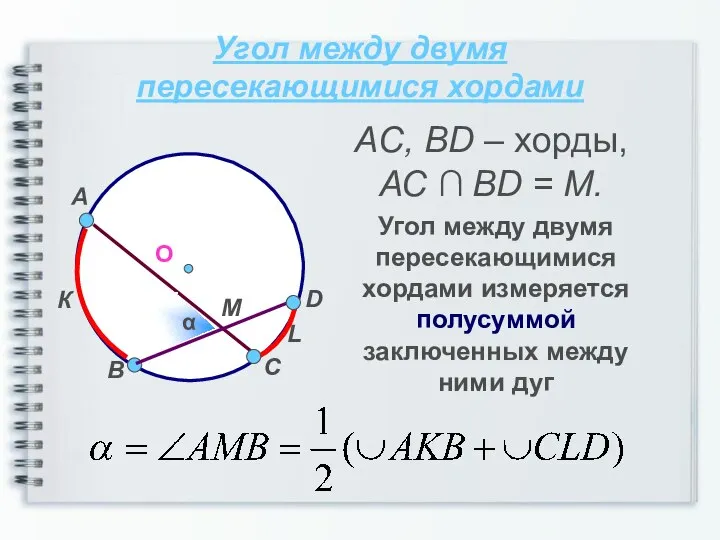
- 8. Угол между двумя пересекающимися хордами Угол между двумя пересекающимися хордами измеряется полусуммой заключенных между ними дуг
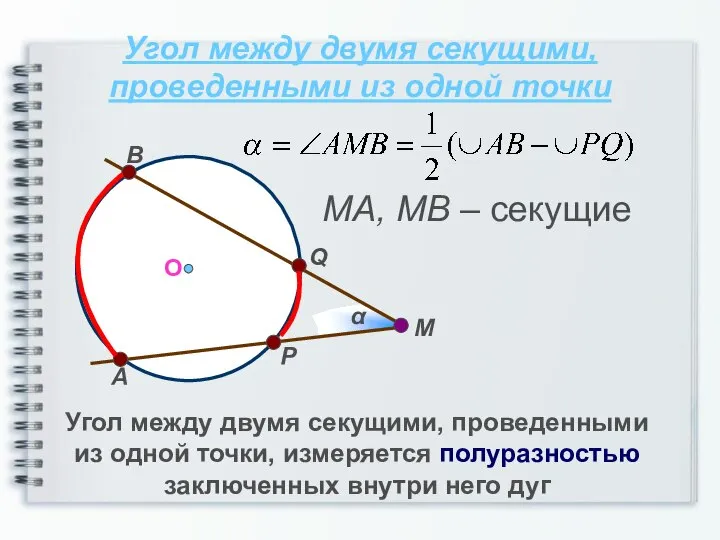
- 9. Угол между двумя секущими, проведенными из одной точки Угол между двумя секущими, проведенными из одной точки,
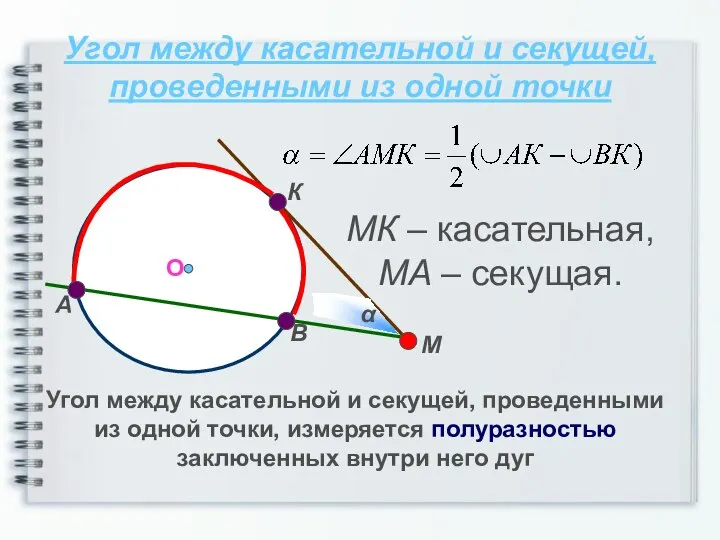
- 10. Угол между касательной и секущей, проведенными из одной точки Угол между касательной и секущей, проведенными из
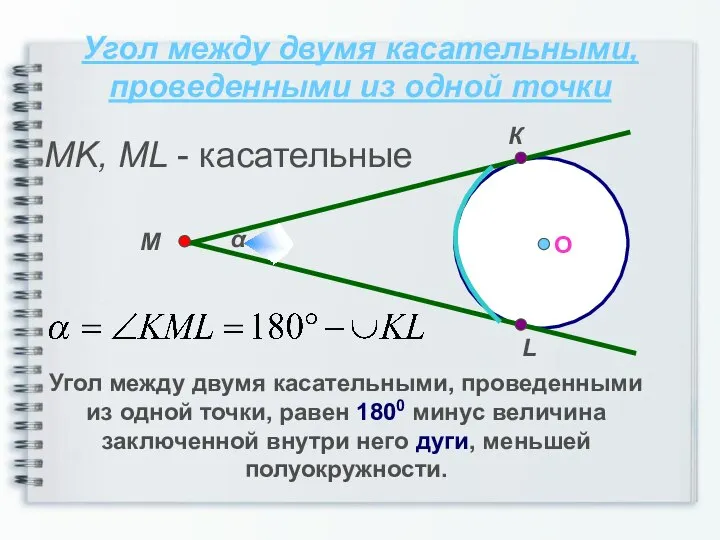
- 11. Угол между двумя касательными, проведенными из одной точки Угол между двумя касательными, проведенными из одной точки,
- 13. Скачать презентацию
 Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Вычисление дробей. Устная работа
Вычисление дробей. Устная работа Вписанная и описанная окружности
Вписанная и описанная окружности Расчет стропильной ноги. Статический расчет
Расчет стропильной ноги. Статический расчет Теория алгоритмов
Теория алгоритмов Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс
Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс Стандартные способы решения уравнений и неравенств (10-11 класс)
Стандартные способы решения уравнений и неравенств (10-11 класс) Математика. Контрольная работа
Математика. Контрольная работа Сумматор. Таблица истинности сумматора
Сумматор. Таблица истинности сумматора Деление одночлена на одночлен
Деление одночлена на одночлен Таблица сложения
Таблица сложения Дифуры 1 порядка
Дифуры 1 порядка Прямоугольный треугольник
Прямоугольный треугольник Логарифмы вокруг нас
Логарифмы вокруг нас Математика в кинематографии
Математика в кинематографии Призма. Теорема
Призма. Теорема Задачи о вкладах и кредитовании (банковских процентах)
Задачи о вкладах и кредитовании (банковских процентах) Правильные многогранники
Правильные многогранники КВН Знакомьтесь: геометрия
КВН Знакомьтесь: геометрия Теория вероятностей
Теория вероятностей Признаки равенства треугольников
Признаки равенства треугольников Делители числа
Делители числа Основы комбинаторики
Основы комбинаторики Замена переменных в определенном интеграле. Лекция №9
Замена переменных в определенном интеграле. Лекция №9 Итоговая диагностика. Математическая вертикаль. 8 класс
Итоговая диагностика. Математическая вертикаль. 8 класс Backpropagation
Backpropagation Процентное отношение
Процентное отношение Прямоугольный параллелепипед
Прямоугольный параллелепипед