Содержание
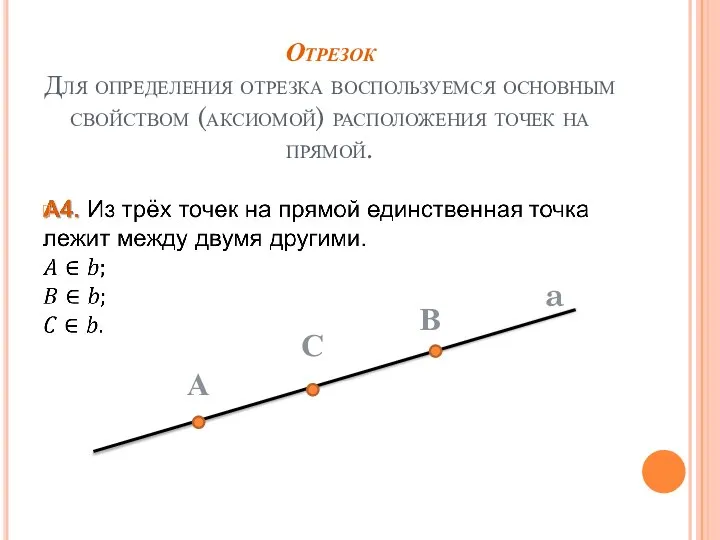
- 2. Отрезок Для определения отрезка воспользуемся основным свойством (аксиомой) расположения точек на прямой.
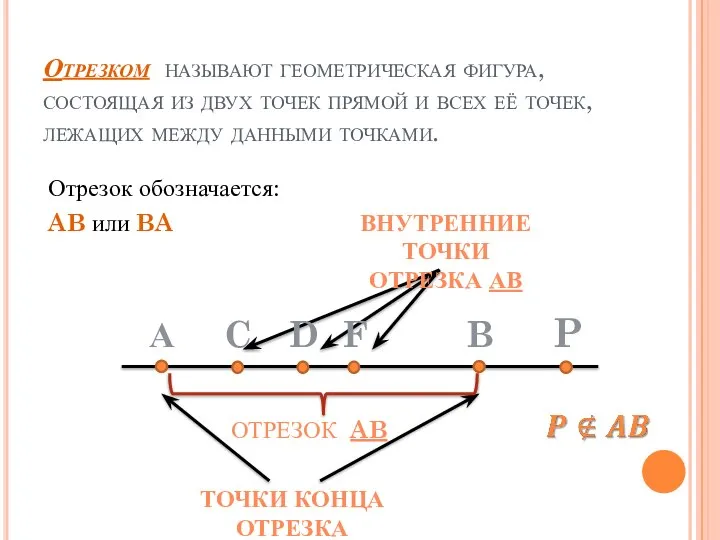
- 3. Отрезком называют геометрическая фигура, состоящая из двух точек прямой и всех её точек, лежащих между данными
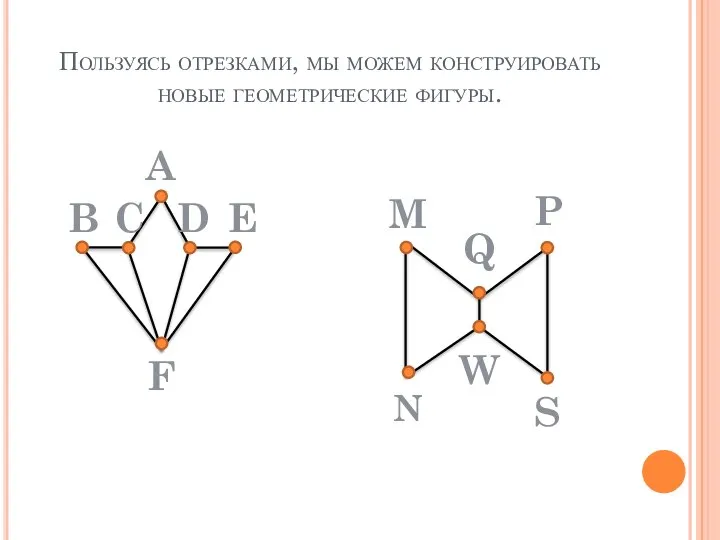
- 4. Пользуясь отрезками, мы можем конструировать новые геометрические фигуры. A E D C B F M Q
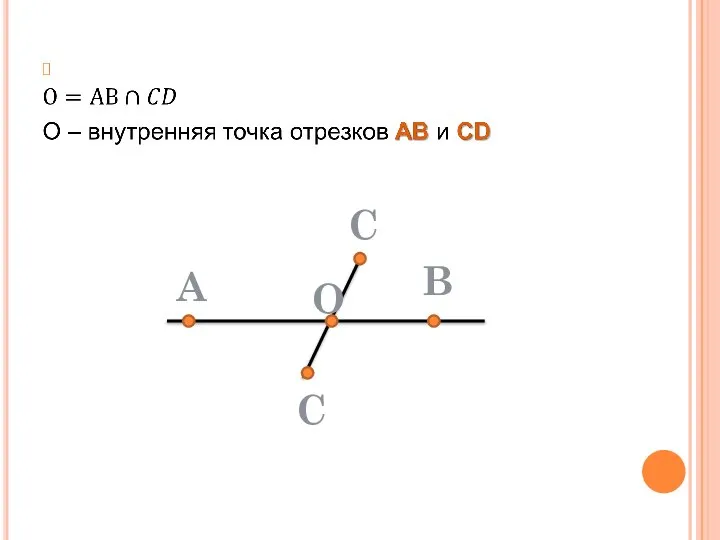
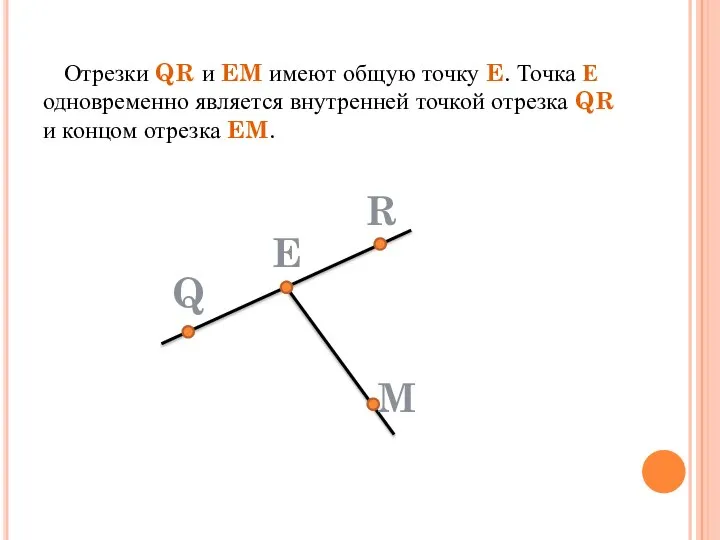
- 6. Отрезки QR и EM имеют общую точку E. Точка Е одновременно является внутренней точкой отрезка QR
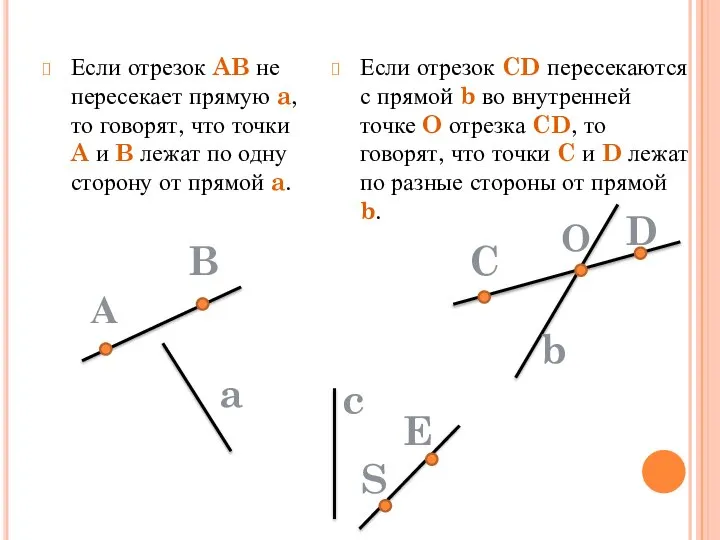
- 7. Если отрезок AB не пересекает прямую a, то говорят, что точки A и B лежат по
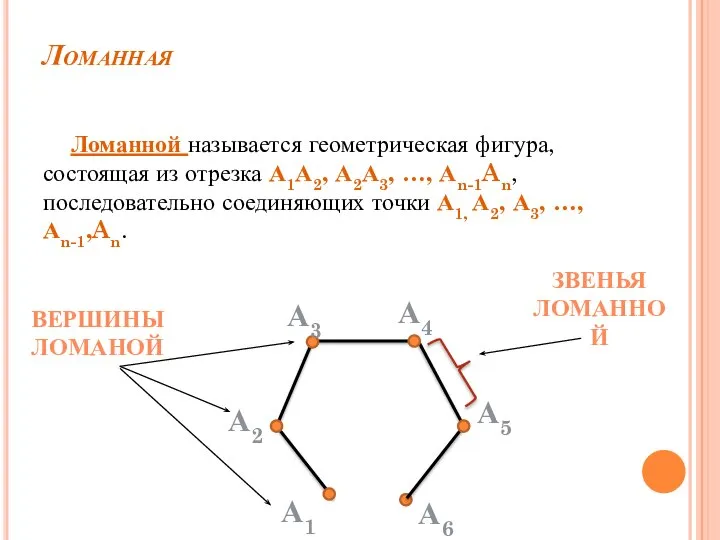
- 8. Ломанная Ломанной называется геометрическая фигура, состоящая из отрезка А1А2, А2А3, …, Аn-1An, последовательно соединяющих точки А1,
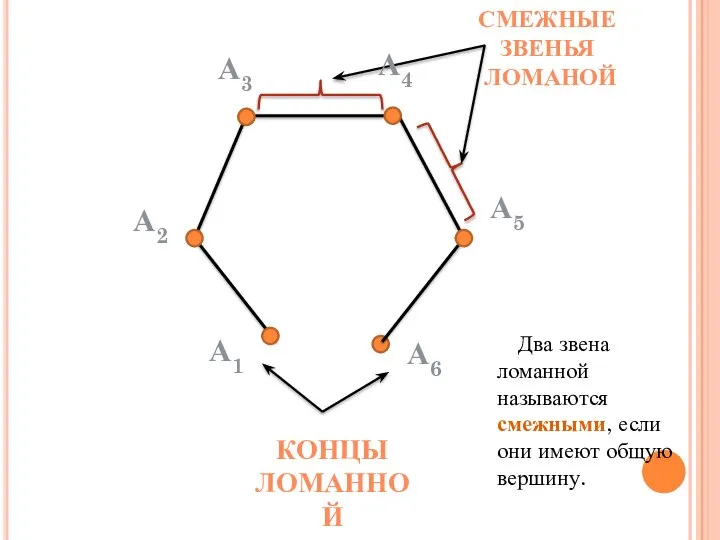
- 9. КОНЦЫ ЛОМАННОЙ СМЕЖНЫЕ ЗВЕНЬЯ ЛОМАНОЙ Два звена ломанной называются смежными, если они имеют общую вершину.
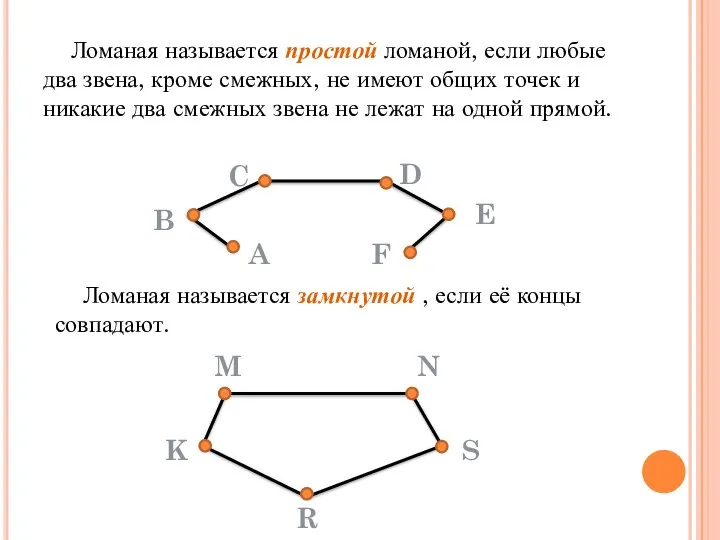
- 10. Ломаная называется простой ломаной, если любые два звена, кроме смежных, не имеют общих точек и никакие
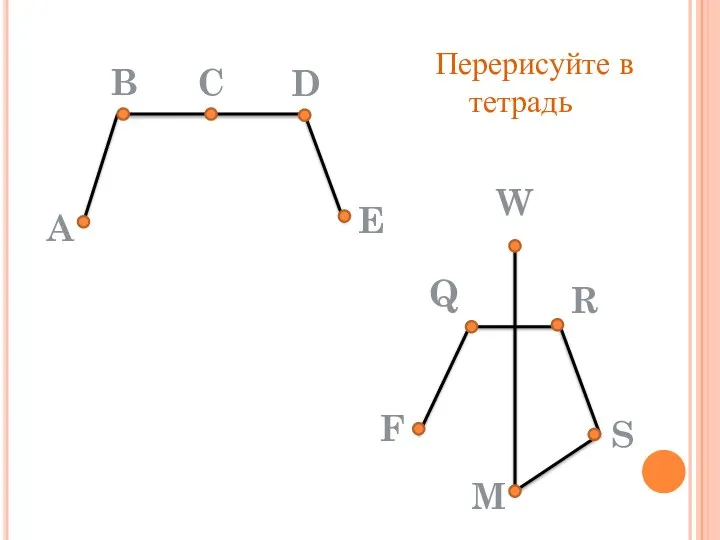
- 11. A B C D E W R Q F M S Перерисуйте в тетрадь
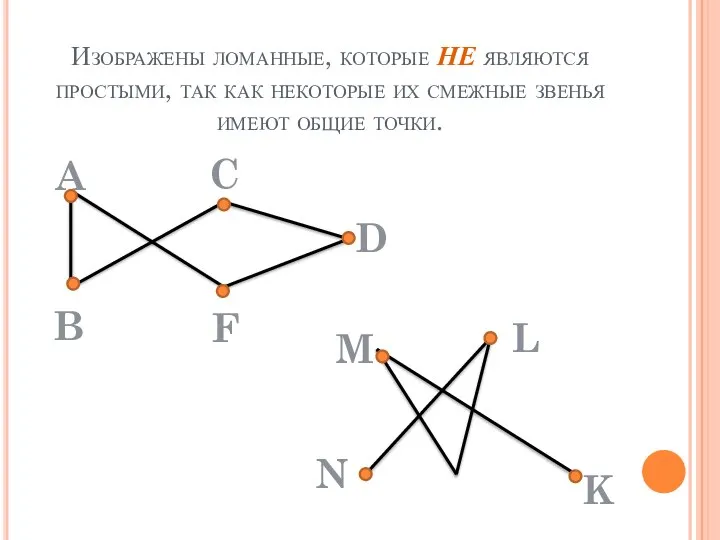
- 12. Изображены ломанные, которые НЕ являются простыми, так как некоторые их смежные звенья имеют общие точки. A
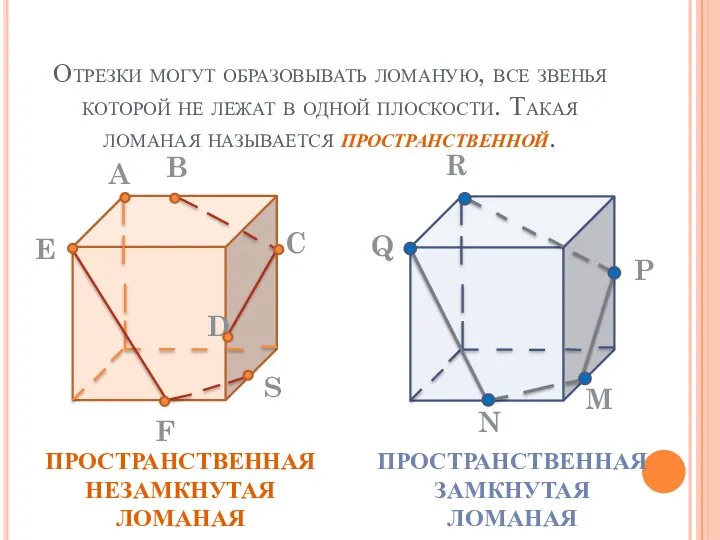
- 13. Отрезки могут образовывать ломаную, все звенья которой не лежат в одной плоскости. Такая ломаная называется пространственной.
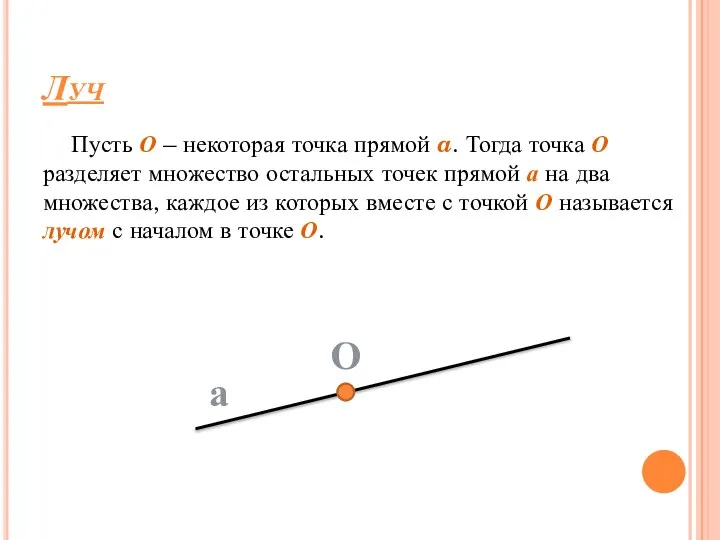
- 14. Луч Пусть О – некоторая точка прямой a. Тогда точка О разделяет множество остальных точек прямой
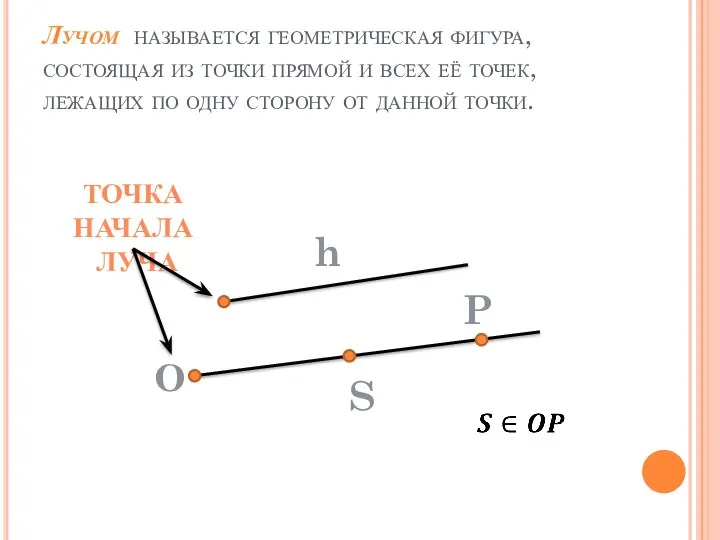
- 15. Лучом называется геометрическая фигура, состоящая из точки прямой и всех её точек, лежащих по одну сторону
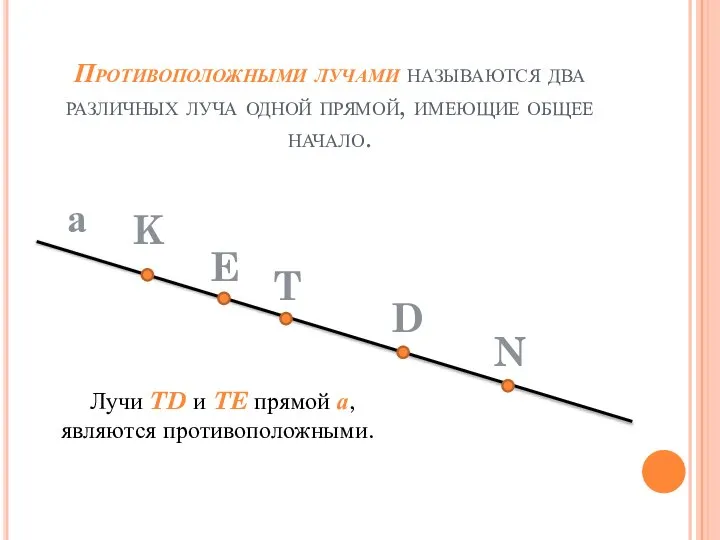
- 16. Противоположными лучами называются два различных луча одной прямой, имеющие общее начало. а E T D Лучи
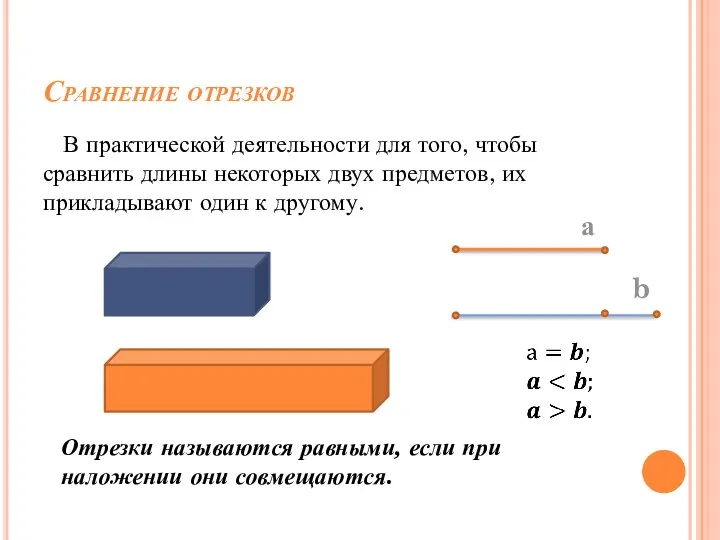
- 17. Сравнение отрезков В практической деятельности для того, чтобы сравнить длины некоторых двух предметов, их прикладывают один
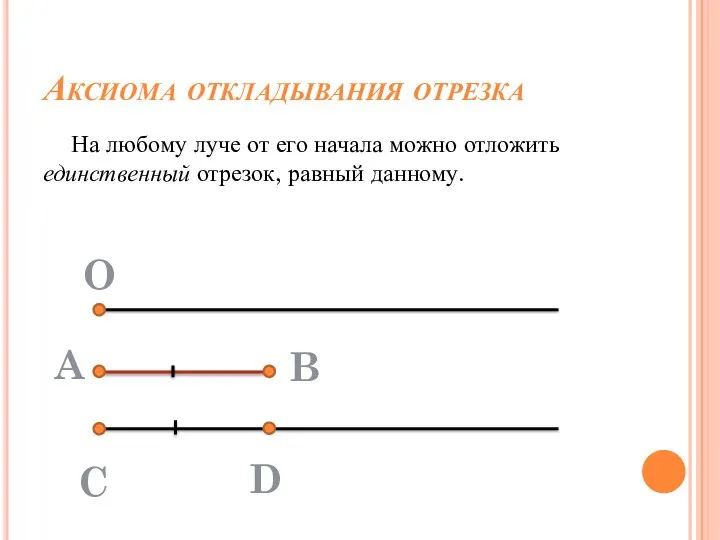
- 18. Аксиома откладывания отрезка На любому луче от его начала можно отложить единственный отрезок, равный данному. O
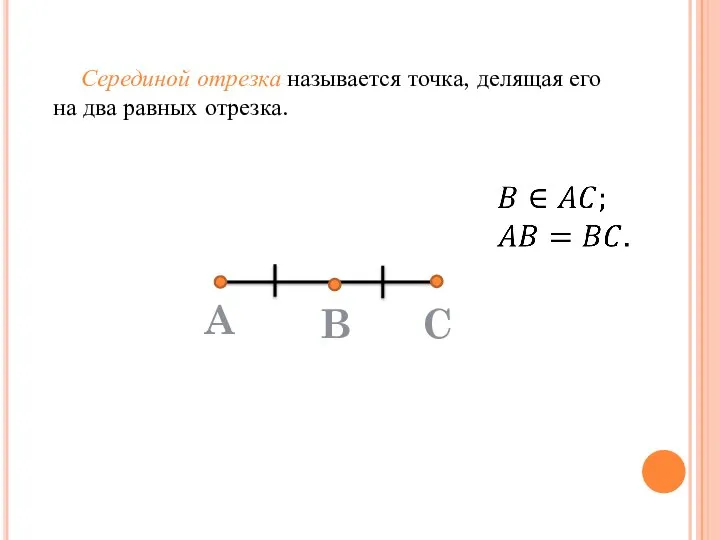
- 19. Серединой отрезка называется точка, делящая его на два равных отрезка.
- 20. Измерение длин отрезков Измерение длин отрезков основано на сравнении их с некоторым отрезком, который принимается за
- 21. Свойства длины отрезков 1) При выбранной единице измерения каждый отрезок имеет длину, которая больше нуля. 2)
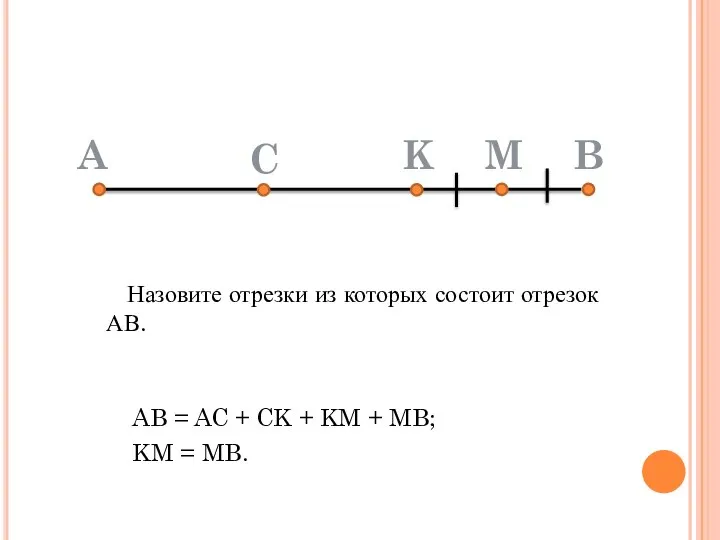
- 22. Назовите отрезки из которых состоит отрезок АВ. A C K M B AB = AC +
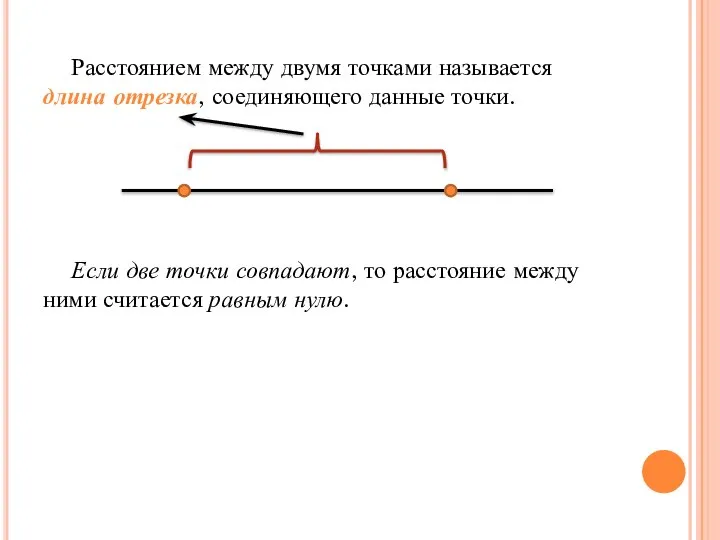
- 23. Расстоянием между двумя точками называется длина отрезка, соединяющего данные точки. Если две точки совпадают, то расстояние
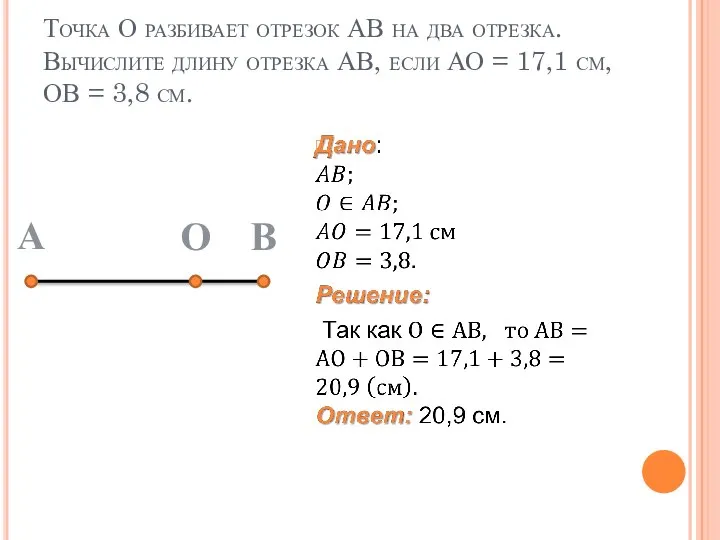
- 24. Точка О разбивает отрезок АВ на два отрезка. Вычислите длину отрезка АВ, если АО = 17,1
- 25. Окружность и круг
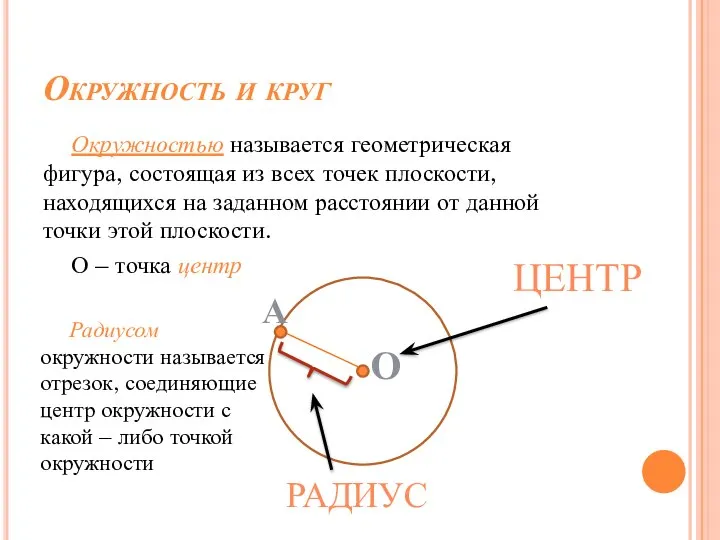
- 26. Окружность и круг Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, находящихся на заданном расстоянии
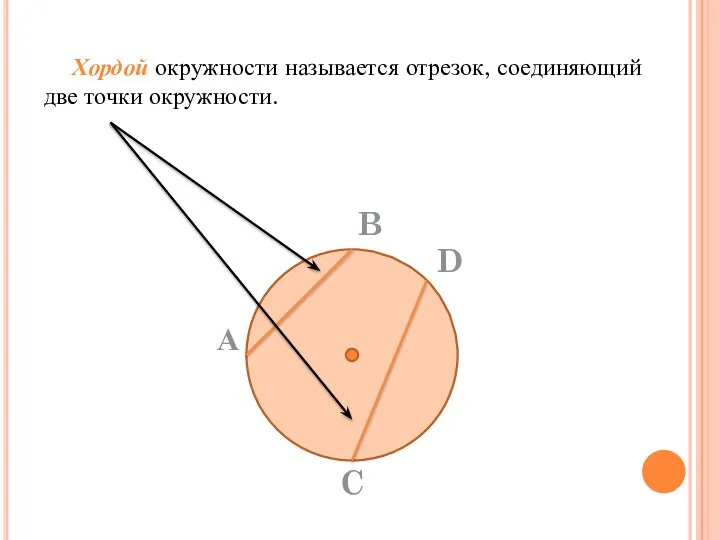
- 27. Хордой окружности называется отрезок, соединяющий две точки окружности.
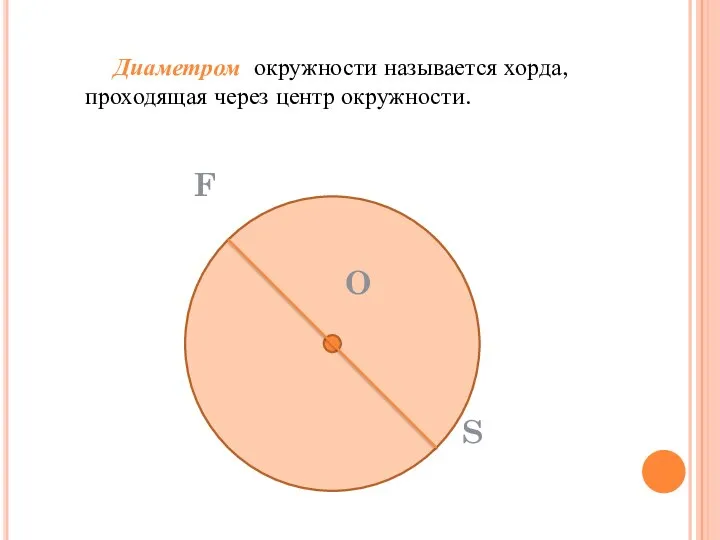
- 28. Диаметром окружности называется хорда, проходящая через центр окружности.
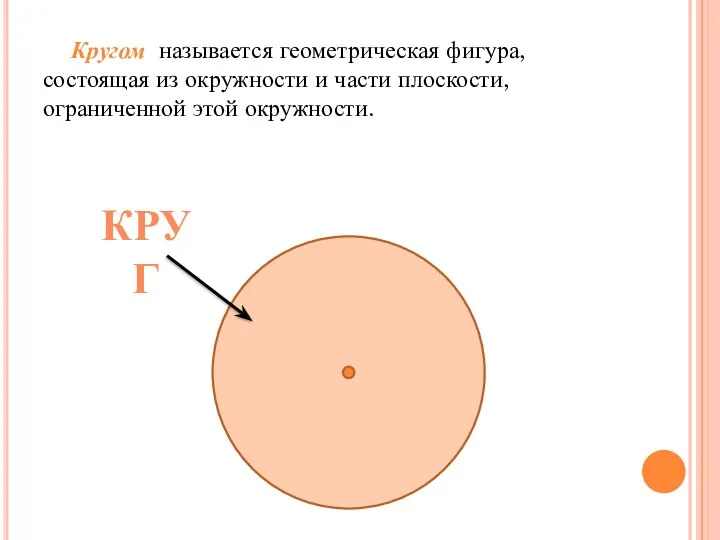
- 30. Кругом называется геометрическая фигура, состоящая из окружности и части плоскости, ограниченной этой окружности. КРУГ
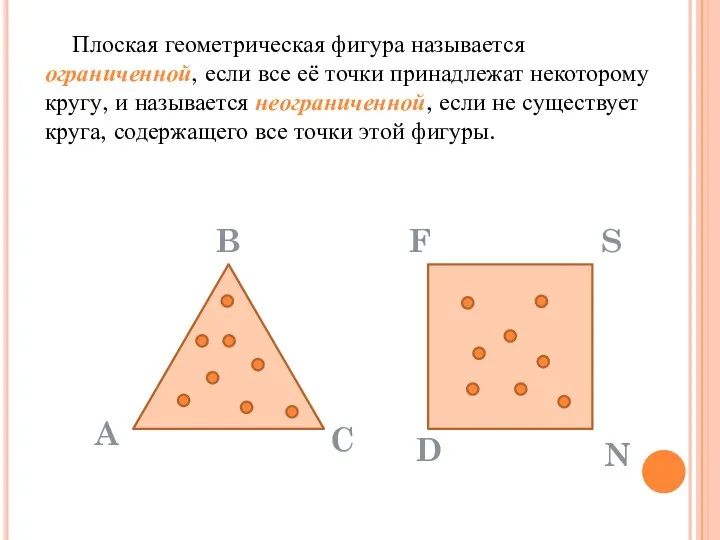
- 31. Плоская геометрическая фигура называется ограниченной, если все её точки принадлежат некоторому кругу, и называется неограниченной, если
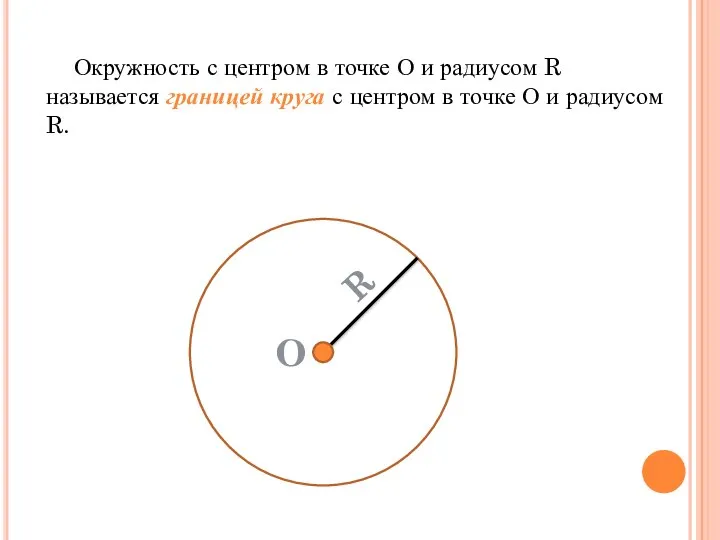
- 32. Окружность с центром в точке О и радиусом R называется границей круга с центром в точке
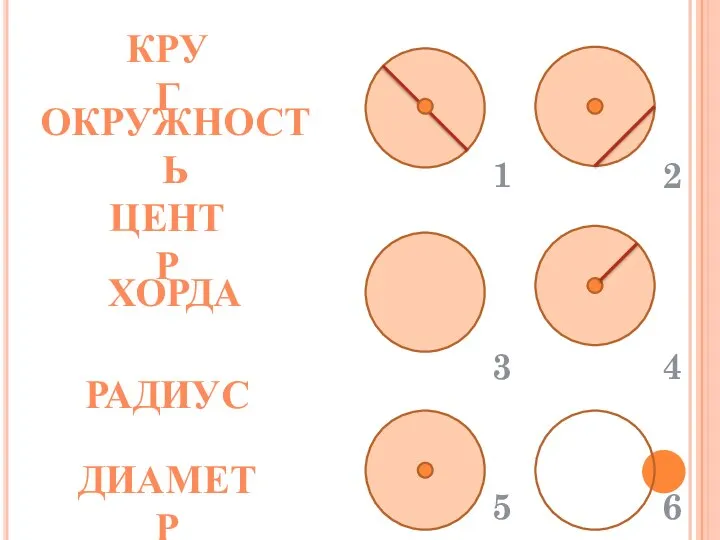
- 33. КРУГ ОКРУЖНОСТЬ ЦЕНТР ХОРДА РАДИУС ДИАМЕТР
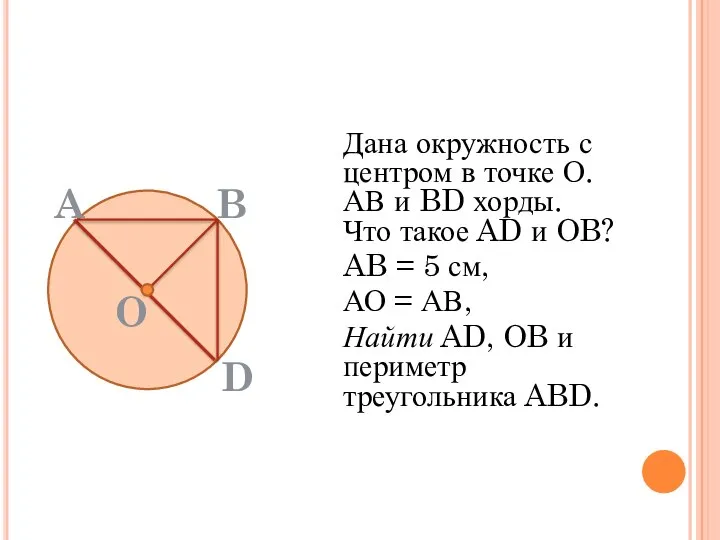
- 34. Дана окружность с центром в точке О. АВ и BD хорды. Что такое AD и OB?
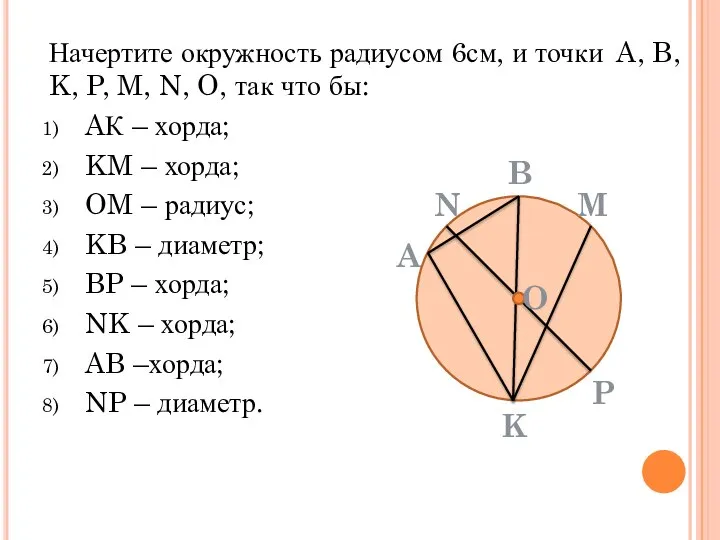
- 35. Начертите окружность радиусом 6см, и точки A, B, K, P, M, N, O, так что бы:
- 37. Скачать презентацию




 Сложение и вычитание векторов
Сложение и вычитание векторов Призмы. Виды призм
Призмы. Виды призм Численное интегрирование
Численное интегрирование Незнайка на планете Математика
Незнайка на планете Математика Решение задач
Решение задач Решение экономических задач
Решение экономических задач Презентация на тему Операции. Обратные операции
Презентация на тему Операции. Обратные операции  Меры длины и веса. Задания
Меры длины и веса. Задания Геометричний метод розв’язування задач лінійного програмування. Методи оптимізації. Лекція №2
Геометричний метод розв’язування задач лінійного програмування. Методи оптимізації. Лекція №2 Тренажер. Смешарики. Сложение в пределах 20
Тренажер. Смешарики. Сложение в пределах 20 Определенный интеграл
Определенный интеграл Сравнение трехзначных чисел
Сравнение трехзначных чисел Статистическая сводка и группировка
Статистическая сводка и группировка Презентация на тему Делимость чисел
Презентация на тему Делимость чисел  Прямоугольный параллелепипед
Прямоугольный параллелепипед Многогранники, символы красоты и совершенства
Многогранники, символы красоты и совершенства Математика в профессиях
Математика в профессиях Математика и режим дня
Математика и режим дня Случаи сложения 470 +80 и вычитания 560-90
Случаи сложения 470 +80 и вычитания 560-90 Умножение десятичной дроби на десятичную дробь
Умножение десятичной дроби на десятичную дробь Видовые числа и коэффициенты формы стволов деревьев
Видовые числа и коэффициенты формы стволов деревьев Площадь многоугольника. Свойства площадей
Площадь многоугольника. Свойства площадей Преимущества урока с ИКТ
Преимущества урока с ИКТ Равенство. Неравенство
Равенство. Неравенство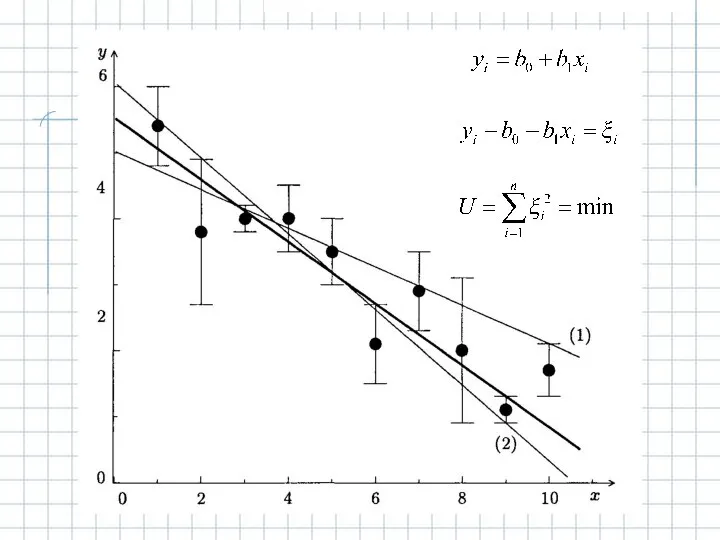 Расчет коэффициентов регрессии (МНК)
Расчет коэффициентов регрессии (МНК) Свойства медианы треугольника
Свойства медианы треугольника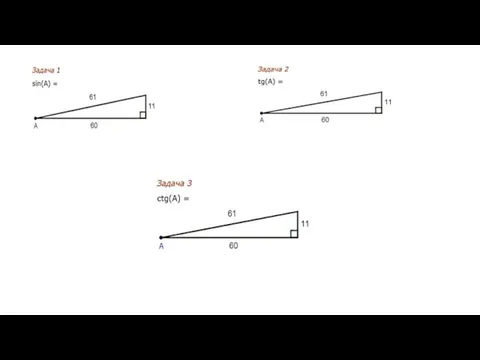 Решение примеров
Решение примеров Свойство описанного четырехугольника
Свойство описанного четырехугольника