Слайд 2Завдання 1. Побудуйте схематично фігури, площі яких виражаються такими інтегралами:

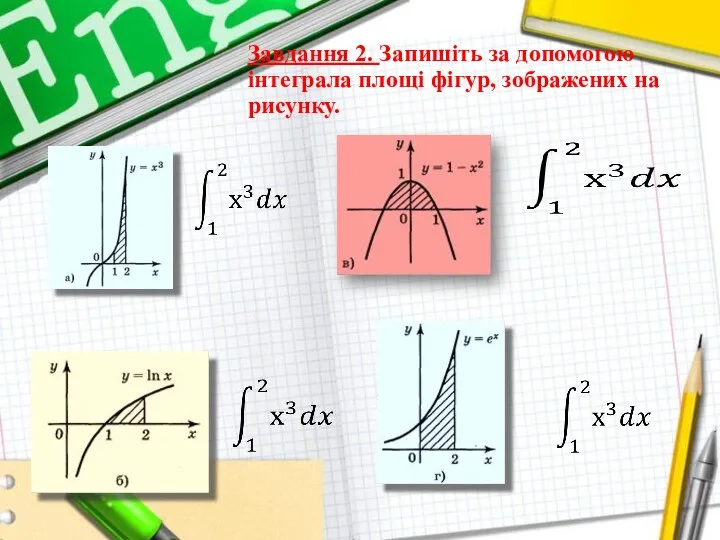
Слайд 3Завдання 2. Запишіть за допомогою інтеграла площі фігур, зображених на рисунку.
Слайд 4Теорема:
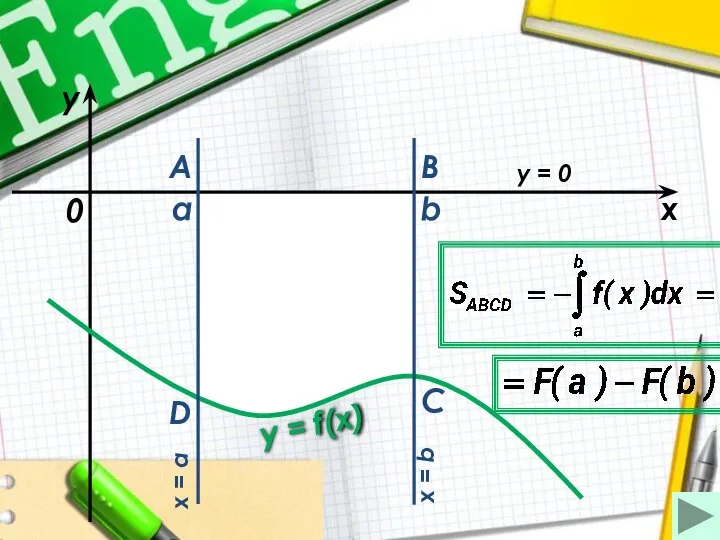
Якщо f-неперервна і невід’ємна на [а, b] функція, а F-її первісна, то
![Теорема: Якщо f-неперервна і невід’ємна на [а, b] функція, а F-її первісна,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1171635/slide-3.jpg)
площа S відповідної криволінійної трапеції дорівнює приросту первісної на відрізку [а, b], тобто
S=F(b)-F(a)
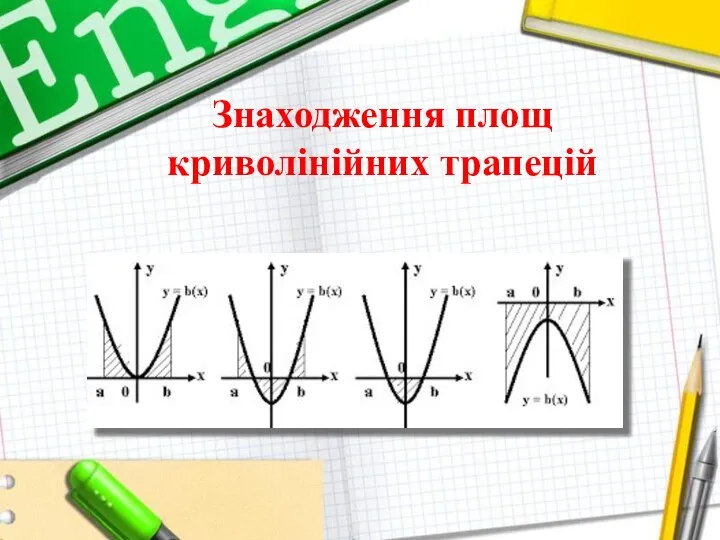
Слайд 5Знаходження площ криволінійних трапецій
Слайд 6 a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y = 0
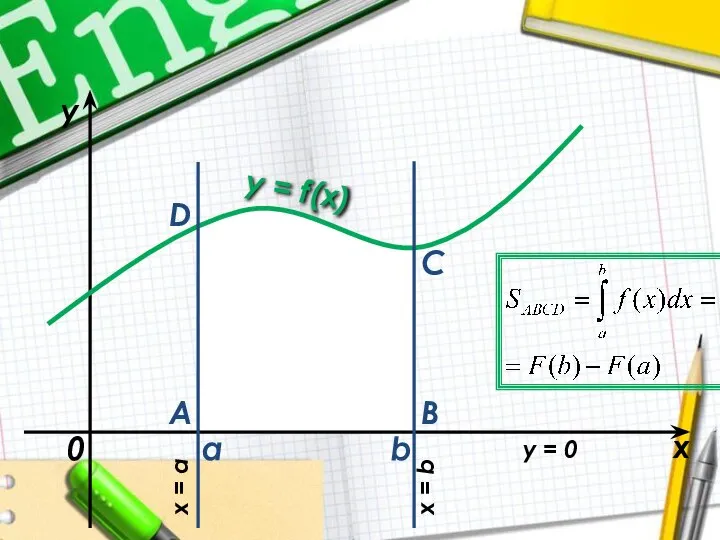
Слайд 7
Знайти площу фігури, обмеженої лініями:

Слайд 8 a
b
x
y
y = f(x)
0
A
B
C
D
x = a
x = b
y = 0
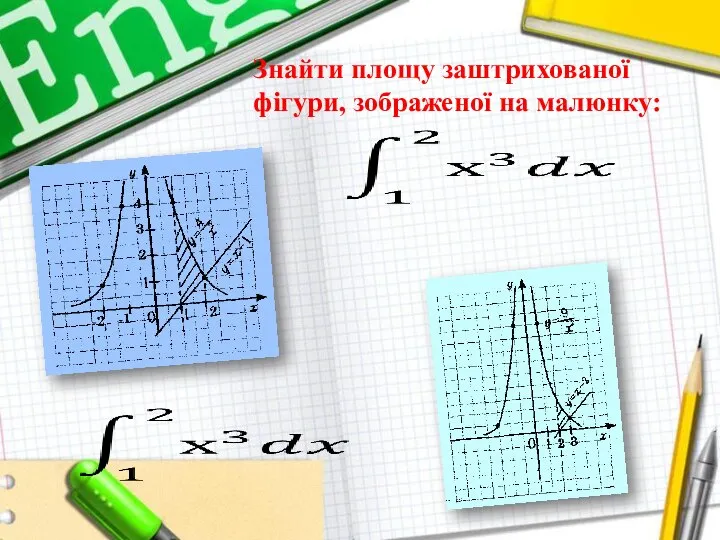
Слайд 11Знайти площу заштрихованої фігури, зображеної на малюнку:


![Теорема: Якщо f-неперервна і невід’ємна на [а, b] функція, а F-її первісна,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1171635/slide-3.jpg)

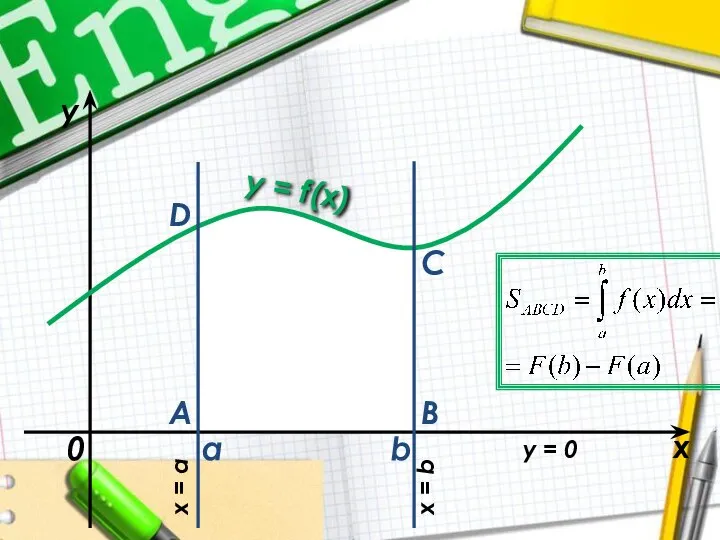





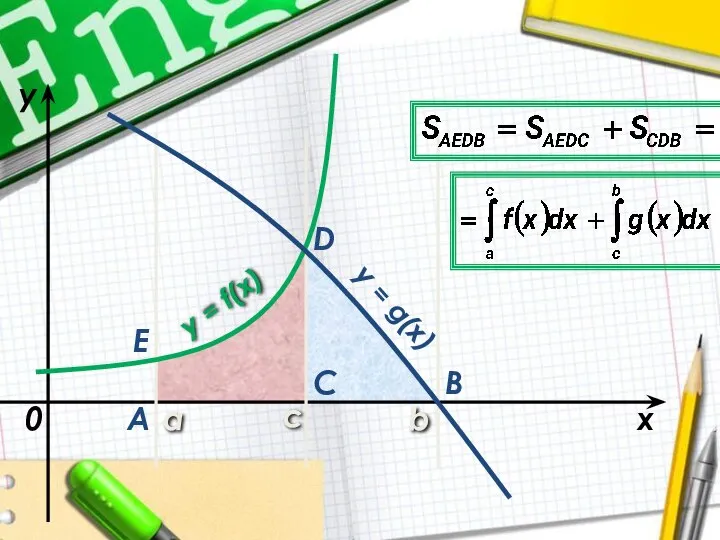
 Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс Величины. Длина
Величины. Длина Случайные величины 14 сен
Случайные величины 14 сен Возникновение первых математических понятий
Возникновение первых математических понятий Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс
Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс Умножение на 1 и 0
Умножение на 1 и 0 Диктант по геометрии
Диктант по геометрии Выбор схемы измерения переменных
Выбор схемы измерения переменных Умножение на 10,100,1000, 0,1, 0,01, 0,001
Умножение на 10,100,1000, 0,1, 0,01, 0,001 Подготовка к блиц-турниру
Подготовка к блиц-турниру Скалярное прозведение векторов
Скалярное прозведение векторов Шифр Цезаря
Шифр Цезаря Сфера и шар
Сфера и шар Многогранники. Призма
Многогранники. Призма Пропорции и проценты
Пропорции и проценты Координаты суммы, разности и произведения вектора на число
Координаты суммы, разности и произведения вектора на число Графический диктант
Графический диктант Презентация на тему Расположение точек относительно осей координат
Презентация на тему Расположение точек относительно осей координат  Найдите высоту и медиану треугольника
Найдите высоту и медиану треугольника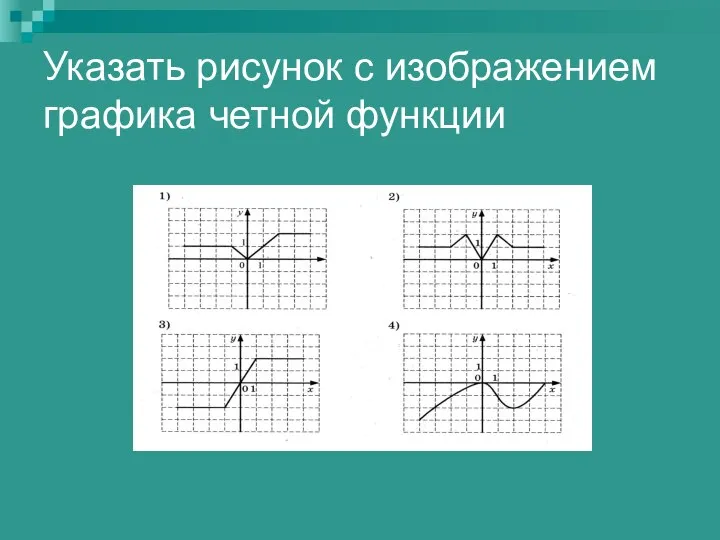 Указать рисунок с изображением графика четной функции
Указать рисунок с изображением графика четной функции Параллелепипед
Параллелепипед Выражение отношения в процентах
Выражение отношения в процентах Задачи на проценты. Схемы
Задачи на проценты. Схемы Решение нелинейных уравнений
Решение нелинейных уравнений Сложение с переходом через десяток. Тренажёр
Сложение с переходом через десяток. Тренажёр Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения
Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика