Содержание
- 2. Цель урока: обобщение и применение аксиом и их следствий к решению задач
- 3. Математический диктант 1). Сформулируйте аксиомы стереометрии: Аксиома 1. через любые три точки, не лежащие на одной
- 4. 2). Заполните пропуски, чтобы получилось верное утверждение: а). Для любой прямой существуют точки, принадлежащие ей, и
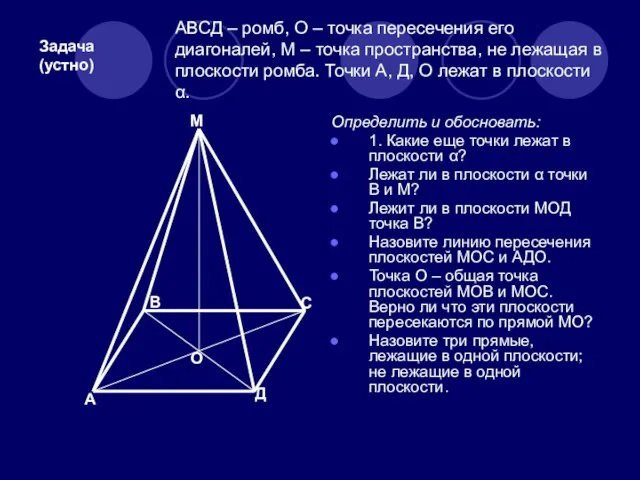
- 5. АВСД – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в
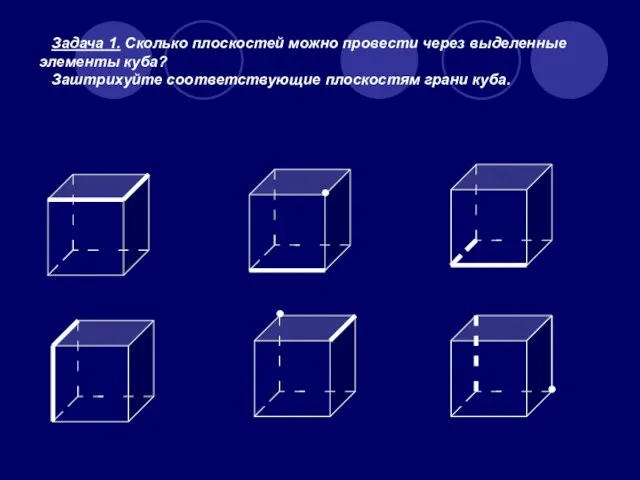
- 6. Задача 1. Сколько плоскостей можно провести через выделенные элементы куба? Заштрихуйте соответствующие плоскостям грани куба. ●
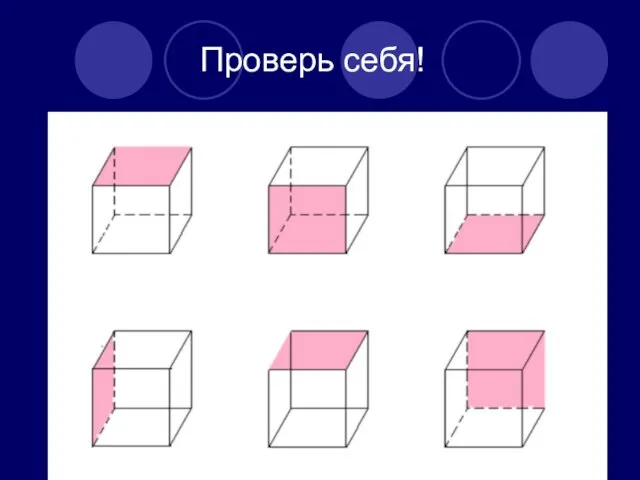
- 7. Проверь себя!
- 8. Задача №2 Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в одной плоскости. Лежат ли
- 9. Задания разного уровня сложности Уровень 1: Точка С – общая точка плоскости альфа и бета. Прямая
- 10. Синквейн Аксиома
- 12. Скачать презентацию






 Занимательная математика
Занимательная математика Способы решения квадратных уравнений
Способы решения квадратных уравнений Презентация. Цилиндр
Презентация. Цилиндр Coordinate plane
Coordinate plane Графы
Графы Расстояние между точкой и прямой
Расстояние между точкой и прямой Презентация на тему Решение уравнений высших степеней
Презентация на тему Решение уравнений высших степеней 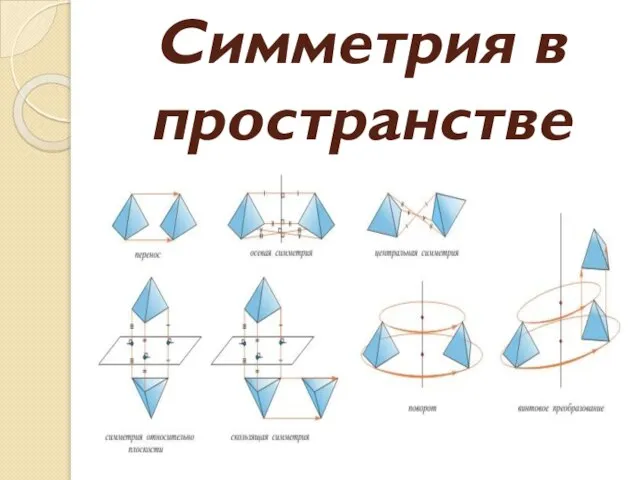 Симметрия в пространстве
Симметрия в пространстве Умножение и деление десятичной дроби на единицу с нулями
Умножение и деление десятичной дроби на единицу с нулями Теоремы синусов и косинусов
Теоремы синусов и косинусов 2_Calculations
2_Calculations Решение задач всех типов на обыкновенные дроби
Решение задач всех типов на обыкновенные дроби Игра-конкурс
Игра-конкурс Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения
Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс Происхождение неевклидовой геометрии
Происхождение неевклидовой геометрии Проецирование точки
Проецирование точки Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними Метод Ньютона
Метод Ньютона История аксиомы
История аксиомы Полезные витамины
Полезные витамины Решение показательных неравенств
Решение показательных неравенств Решение уравнений
Решение уравнений Сечение тетраэдра
Сечение тетраэдра Прямая Эйлера
Прямая Эйлера Алгоритм нахождения интервалов выпуклости и точек перегиба
Алгоритм нахождения интервалов выпуклости и точек перегиба Золотое сечение
Золотое сечение Пушкин и математика
Пушкин и математика