Многогранники. Призма

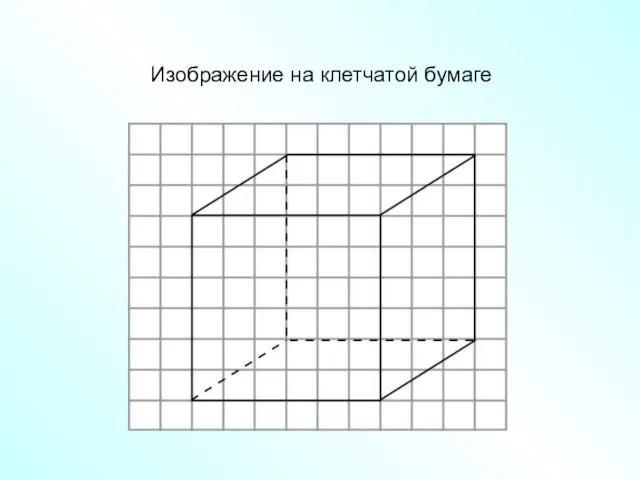
Изображение на клетчатой бумаге

Поверхность, составленная из двух равных параллелограммов, лежащих в параллельных плоскостях, и четырёх параллелограммов, называется параллелепипедом.
ПАРАЛЛЕЛЕПИПЕД

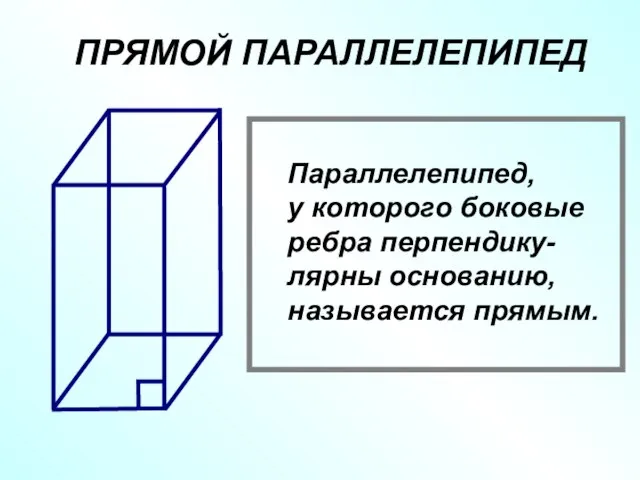
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД
Параллелепипед,
у которого боковые
ребра перпендику-
лярны основанию,
называется прямым.

А
В
С
С1
А1
В1
Д1
Д
10. В прямоугольном
параллелепипеде
все шесть граней –
прямоугольники.
20. Все двугранные углы
прямоугольного
параллелепипеда –
прямые.

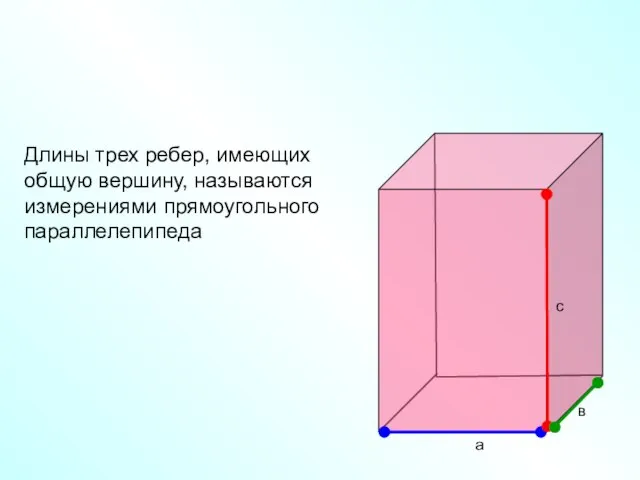
Длины трех ребер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда
в
а
с

C
а
b
с
B
A
D
B1
C1
D1
A1
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
d2 = a2 + b2 + с2

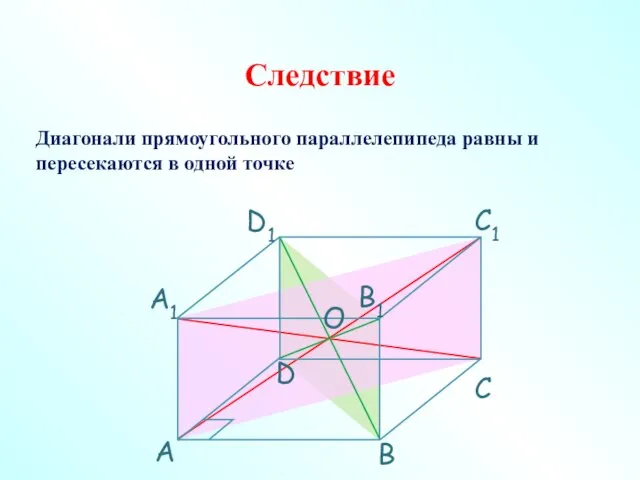
Диагонали прямоугольного параллелепипеда равны и пересекаются в одной точке
Следствие
О

Тетраэдр – поверхность, составленная из четырех треугольников.

Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.
Понятие многогранника
Призма

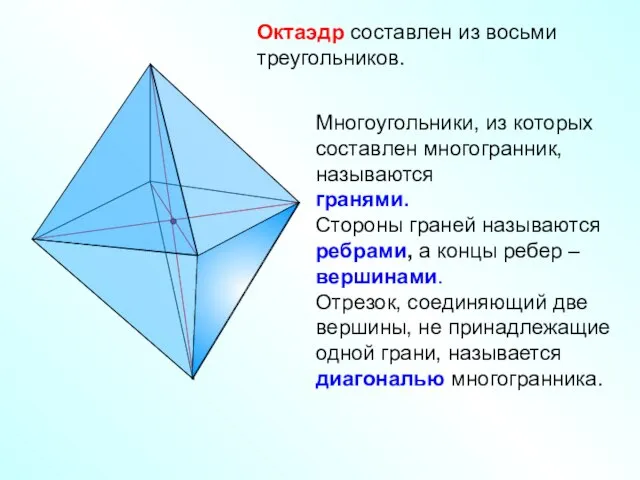
Октаэдр составлен из восьми треугольников.
Многоугольники, из которых составлен многогранник, называются
гранями.
Стороны граней называются ребрами, а концы ребер – вершинами.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

Многогранник, в каждой вершине которого сходится пять правильных треугольников называется икосаэдром.
ИКОСАЭДР

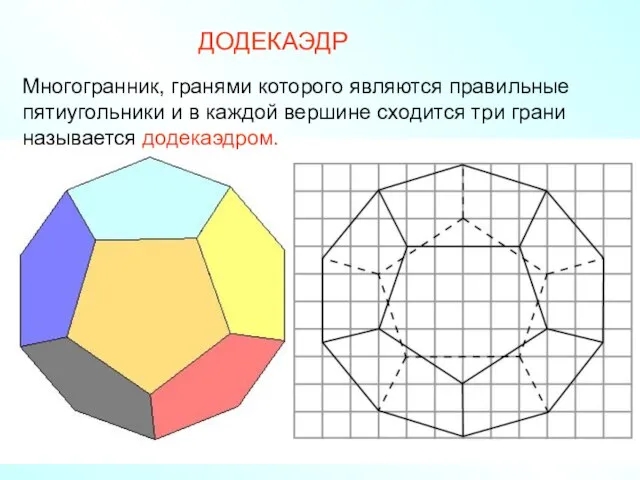
Многогранник, гранями которого являются правильные пятиугольники и в каждой вершине сходится три грани называется додекаэдром.
ДОДЕКАЭДР

Выпуклые и невыпуклые многогранники

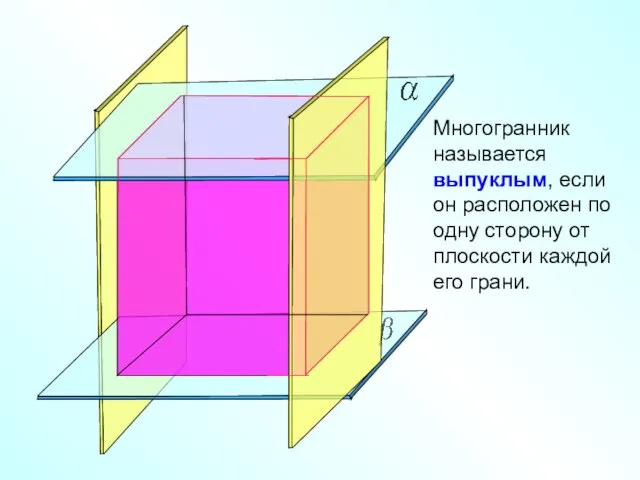
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.

Невыпуклый многогранник

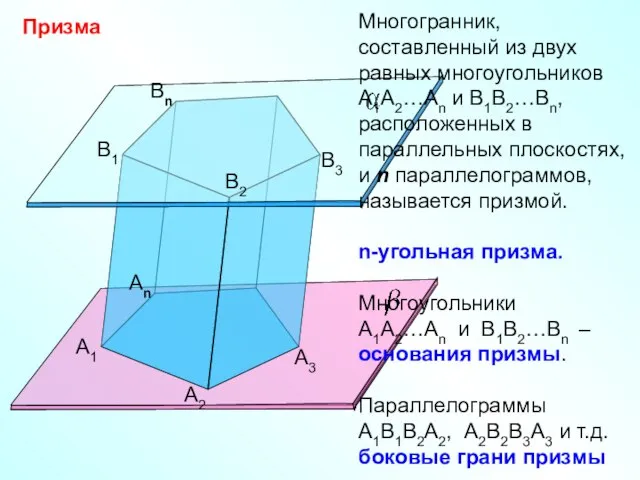
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.
n-угольная призма.
Многоугольники
А1А2…Аn и В1В2…Вn – основания призмы.
Параллелограммы А1В1В2А2, А2В2В3А3 и т.д. боковые грани призмы

Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Отрезки А1В1, А2В2 и т.д. -
боковые ребра призмы
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

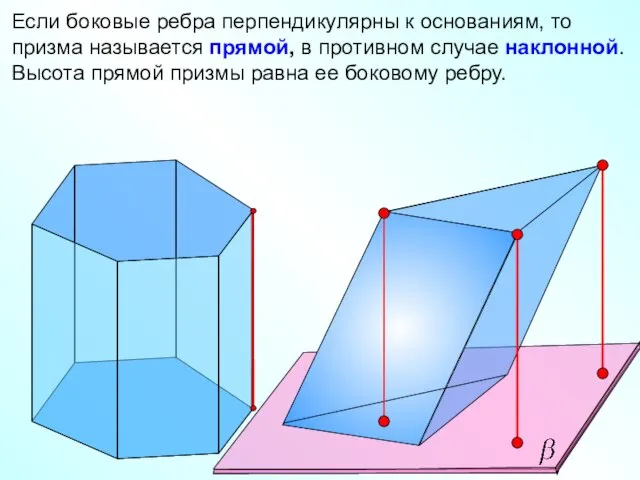
Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.

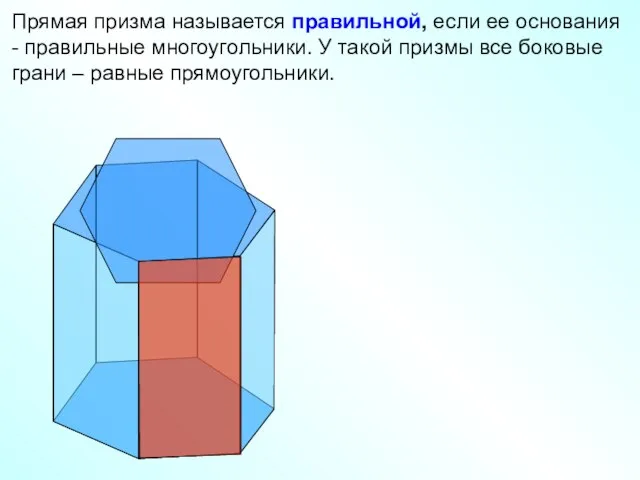
Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

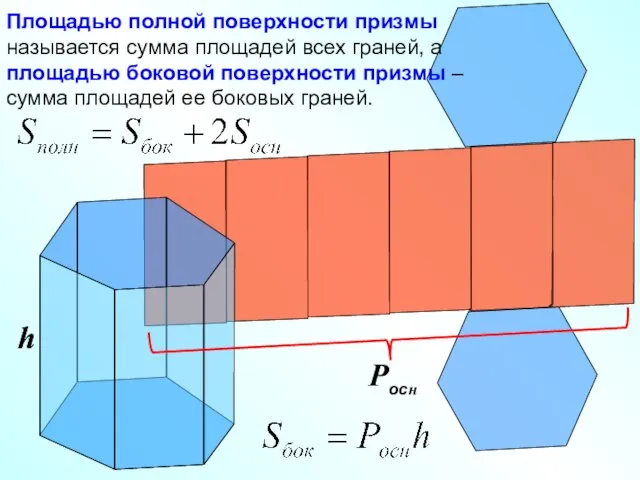
Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней.
h
h
Pocн

В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.
№ 219.
В
С
А1
D1
С1
В1
?
D
А
12 см
5 см