Тригонометрические функции, их свойства и графики

Общая схема исследования функции
Область определения
Нули функции
Промежутки знакопостоянства
Четность-нечетность.
Монотонность
Экстремумы
Область значений

Кроссворд

Кроссворд

«Тригонометрические функции, их свойства и графики»

у
х
О
-
-
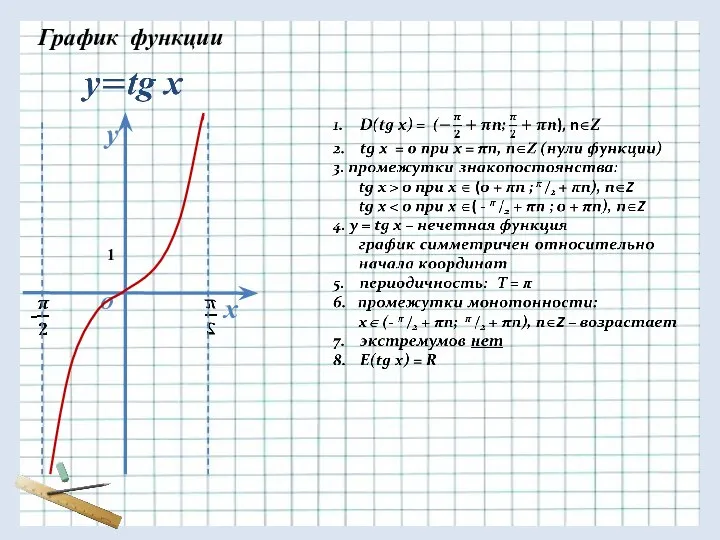
График функции
1
D(sin x) = (-∞; +∞)
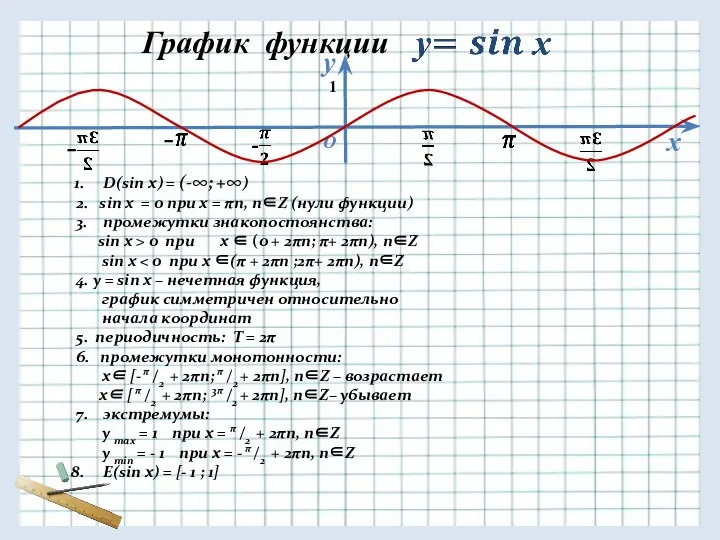
2. sin x = 0 при х = πn, n∈Z (нули функции)
3. промежутки знакопостоянства:
sin x > 0 при x ∈ (0 + 2πn; π+ 2πn), n∈Z
sin x < 0 при x ∈(π + 2πn ;2π+ 2πn), n∈Z
4. y = sin x – нечетная функция,
график симметричен относительно
начала координат
5. периодичность: T = 2π
6. промежутки монотонности:
x∈ [- π /2 + 2πn; π /2 + 2πn], n∈Z – возрастает
x∈ [ π /2 + 2πn; 3π /2 + 2πn], n∈Z– убывает
7. экстремумы:
y max = 1 при х = π /2 + 2πn, n∈Z
y min = - 1 при х = - π /2 + 2πn, n∈Z
E(sin x) = [- 1 ; 1]

у
х
О
-
-
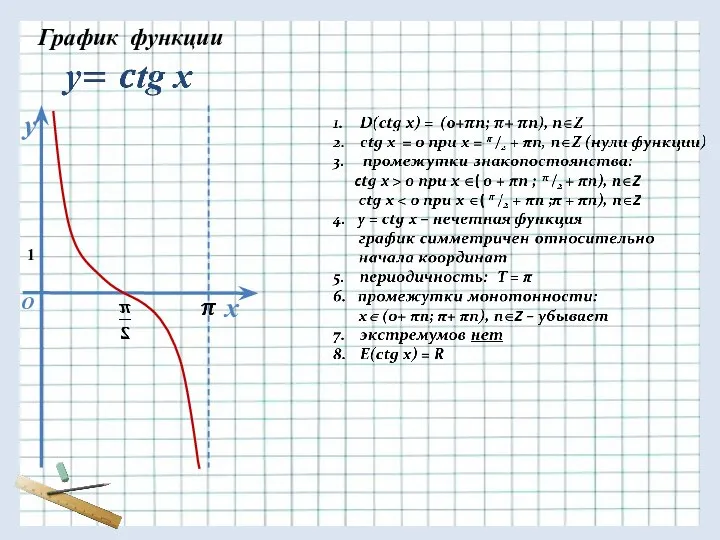
График функции
1
D(cos x) = (-∞; +∞)
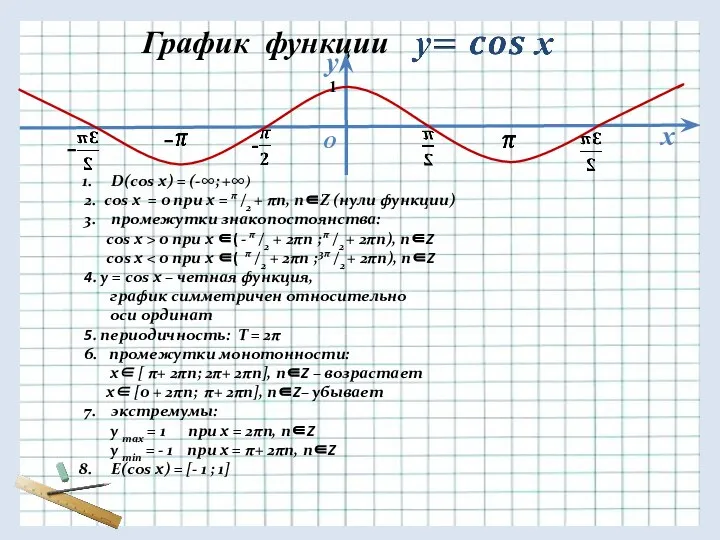
2. cos x = 0 при х = π /2 + πn, n∈Z (нули функции)
3. промежутки знакопостоянства:
cos x > 0 при x ∈( - π /2 + 2πn ; π /2 + 2πn), n∈Z
cos x < 0 при x ∈( π /2 + 2πn ; 3π /2 + 2πn), n∈Z
4. y = cos x – четная функция,
график симметричен относительно
оси ординат
5. периодичноcть: T = 2π
6. промежутки монотонности:
x∈ [ π+ 2πn; 2π+ 2πn], n∈Z – возрастает
x∈ [0 + 2πn; π+ 2πn], n∈Z– убывает
7. экстремумы:
y max = 1 при х = 2πn, n∈Z
y min = - 1 при х = π+ 2πn, n∈Z
E(cos x) = [- 1 ; 1]

у
х
О
График функции
1

у
х
О
График функции
1