Содержание
- 8. Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и
- 9. В развитии теории вероятностей весьма большую роль играли задачи, связанные с азартными играми, в первую очередь
- 10. Возникновение теории вероятностей в современном смысле слова относится к середине XVII века и связано с исследованиями
- 11. События и действия над ними
- 12. СЛУЧАЙНОЕ - НЕВОЗМОЖНОЕ - РАВНОВОЗМОЖНЫЕ - ДОСТОВЕРНОЕ - событие, которое может произойти, а может и не
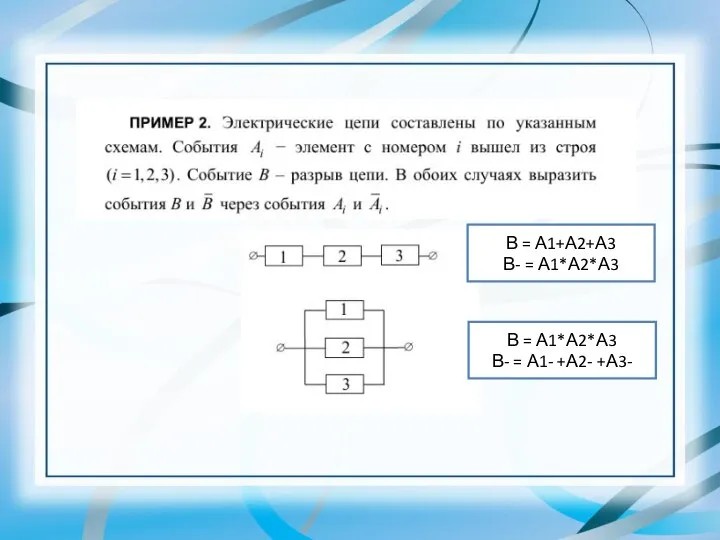
- 18. В = А1+А2+А3 В- = А1*А2*А3 В = А1*А2*А3 В- = А1- +А2- +А3-
- 22. Пример. Андрей, Роман, Максим и Сергей бросили жребий, кому быть вратарем. Найти вероятность того, что вратарем
- 23. Задание В чемпионате по гимнастике участвуют 64 спортсменки: 20 из Японии, 28 из Китая, остальные —
- 24. Задание В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел не выпадет ни
- 25. Игральный кубик бросили один раз. Какова вероятность того, что выпадает не менее 4 очков? Решение: Бросаем
- 44. Практическое задание Задача 1. Семь карточек с буквами А, А, А, Б, Б, Р, Н, перемешивают
- 45. Практическое задание Задача 4. Вероятность попадания в мишень для первого стрелка равна 0,65, для второго –
- 46. Практическое задание Задача 7
- 48. Скачать презентацию











































 Теорема Пифагора
Теорема Пифагора Степень числа
Степень числа Тема Функция у = ах2 и её график
Тема Функция у = ах2 и её график Решение задач и уравнений
Решение задач и уравнений Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Задачи о дачном участке
Задачи о дачном участке Симметрия в пространстве
Симметрия в пространстве Математика. Задачи
Математика. Задачи Игра - тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра - тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Теорема Байеса
Теорема Байеса Презентация на тему Что такое функция? 7 класс
Презентация на тему Что такое функция? 7 класс  Помогают законы. 5 - 7 класс
Помогают законы. 5 - 7 класс Отбор корней в тригонометрическом уравнении
Отбор корней в тригонометрическом уравнении Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5? Презентация на тему Решение задач по теории вероятностей
Презентация на тему Решение задач по теории вероятностей  Метапредметное обучение как инновационный процесс в современном математическом образовании
Метапредметное обучение как инновационный процесс в современном математическом образовании Существование треугольника, равного данному (7 класс)
Существование треугольника, равного данному (7 класс) Подготовка к контрольной работе по математике
Подготовка к контрольной работе по математике Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Построение сечений в параллелепипеде
Построение сечений в параллелепипеде Средняя линия треугольника
Средняя линия треугольника Натуральный ряд
Натуральный ряд подготовка к ВПР
подготовка к ВПР Анализ геометрической формы предмета (7 класс)
Анализ геометрической формы предмета (7 класс) Преобразование графиков вида у=f(х±а)
Преобразование графиков вида у=f(х±а) Методика ознакомления обучающихся с геометрическими фигурами (прямой, ломаной) и их свойствами
Методика ознакомления обучающихся с геометрическими фигурами (прямой, ломаной) и их свойствами Прямоугольный треугольник
Прямоугольный треугольник Все ли в мире состоит из многогранников
Все ли в мире состоит из многогранников