Бравэ Пирсонның сызықтық корреляция коэффициенті

Корреляциялық талдау
«Корреляция» термині өзара байланыс, өзара тәуелділік мағынасын білдіреді. Корреляция туралы айтқанда "корреляциялық байланыс" термині қатар қолданылады.
Корреляциялық байланыс – бұл екі белгінің немесе бірнеше белгінің (көпмүшелі корреляциялық байланыс) бір – бірімен сәйкестене өзгеруі.
Корреляциялық талдау Х және кездейсоқ шамаларының арасындағы байланыстың дәрежесін анықтаумен айналысады.
Екі кездейсоқ шамалар үшін тәжірибе нәтижесінде алынған деректердің корреляциялық талдауы мынадай негізгі тәсілдерді қарастырады:
1. Корреляциялық таңдама коэффициентін есептеу.
2. Корреляциялық кесте құру.
3. Байланыс мәнділігі жөніндегі статистикалық жорамалды тексеру.
Анықтама. Егер және регрессия функцияларының екеуі де сызықтық болса, онда Х және кездейсоқ шамаларының арасындағы корреляциялық тәуелділік сызықтық корреляция деп аталады.
Регрессия дегеніміз – бір тәуелді айнымалы (әдетте Y арқылы белгіленеді) және басқа айнымалылар қатары (тәуелсіз айнымалылар деп аталатын) арасындағы байланыстың күші мен сипатын анықтауға тырысатын қаржы, инвестициялау және басқа пәндерде қолданылатын статистикалық әдіс.

«Корреляция» терминін алғаш
рет француз палеонтологы Ж. Кювье енгізді, ал статистикада оны
Ф. Гальтон алғаш қолданды.
Корреляциялық талдау
Ж. Кювье
(1769 - 1832)
Ф. Гальтон
(1822 - 1911)
Корреляцилық талдау – бұл екі немесе одан көп кездейсоқ шамалардың арасындағы байланыстың тығыздығын және бағытын анықтайтын сандық әдіс.

Корреляция коэффициенті
Байланыстың күшін бағалау үшін корреляция теориясында анғылшын
статистигі Чеддоктың шкаласы қолданылыды
Корреляция коэффициенті
Корреляция коэффициенті – байланыстың күшін және оның бағытын сипаттайтын, [-1, 1] аралығынды мәндерін қабылдайтын көрсеткіш.
Оны символмен r деп белгілейді.
Корреляция коэффициенті - бір айнымалыны екіншісін біле отырып, қаншалықты жақсы болжауға болатынын бағалайтын статистика;Мысалы,адамдардың биіктігін білу арқылы олардың салмағын болжауға болатынын айтайық.

Корреляция оң (+) және теріс (-) болуы мүмкін. Корреляция белгісі екі айнымалының оң корреляциямен байланысты екенін көрсетеді (екі айнымалының мәні бір уақытта өседі немесе төмендейді) немесе теріс корреляция (бір айнымалының екіншісі кеміген сайын артады). Мысалы, студенттің сабаққа келмеуінің семестрдің соңындағы балмен -0.40 корреляциясы бар делік (сабақтан қалу неғұрлым көп болса, балл соғұрлым төмен). Екінші жағынан, алынған балл мен қатысқан сабақтар саны арасындағы корреляция +0.40 болады. Облигацияның беріктігі бірдей, бірақ оның белгісі сабақтарға қатыспағанымызды немесе сабаққа қатысқанымызға байланысты.

Корреляциялық байланыс
Корреляция коэффициенті – салыстырылатын екі статистикалық белгілердің арасындағы байланыс күшінің математикалық көрсеткіші. Корреляция қандай формуламен есептелінсе де, оның мәні ылғи да -1 және +1 шегінде болады. Коэффициенттің шеткі мәнінің мағынасын былай түсіну керек:
егерде коэффициенттің мәні -1-ге тең болса, онда байланыс кері
пропорционалдық тип бойынша функционалды деп саналады;
егерде ол +1-ге тең болса, онда белгілер арасындағы байланыс тура (тікелей) пропорционалдылық тәуелділік типі бойынша біржақты (функционалды,
статистикалы емес);
егерде оның мәні нольге тең болса, онда салыстырылатын белгілердің
арасындағы байланыс нолдік шамаға тең немесе байланыс жоқ дегенді
білдіреді.

Жұптасқан Пирсонның
корреляция коэффициенті
Сызықты (жұптасқан Пирсонның) корреляция коэффициенті –
байланыстың күшін және бағытын сипаттайтын көрсеткіш:
мұндағы rxy – корреляция коэффициенті,
х, у – корреляцияланатын қатар,
, - орташа шамалар.
Жұптасқан корреляция коэффициенті параметрлік коэффициент болып
табылады.

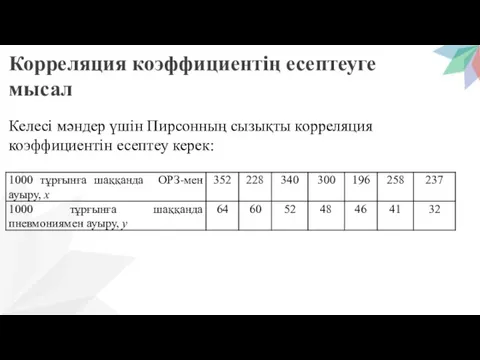
Корреляция коэффициентің есептеуге
мысал
Келесі мәндер үшін Пирсонның сызықты корреляция
коэффициентін есептеу керек:

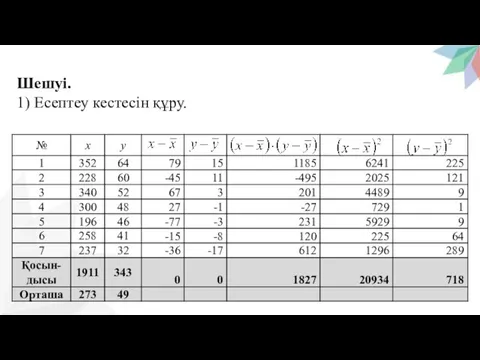
Шешуі.
1) Есептеу кестесін құру.

2) Корреляция коэффициентін есептеу керек:
3) Алынған нәтижені талдау: қарастырылған белгілердің арасындағы байланыс тура, қалыпты.
4) Корреляция коэффициентінің орташа қателігін есептеу:
Корреляция коэффициенті өзінің орташа қателігінен 3 есе артық
болмағандықтан сенімді емес.

КОРРЕЛЯЦИЯЛЫҚ ТАЛДАУ
Орындаған: Санақ Айгерім

МЫСАЛЫ
Алынған тест деректері бойынша мектеп оқушыларының агрессивтілігі мен IQ екі айнымалысы арасындағы байланысты анықтауымыз керек.

1. X және Y мәндерінің қосындысын есептеңіз
2. X} және Y үшін орташа арифметикалық мәнді есептеңіз
3. X және Y үшін орташа арифметикалық мәннен тексерілген әрбір ауытқуды есептеңіз.

4. Содан кейін әрбір ауытқуды квадраттаймыз:
5. Содан кейін ауытқулардың квадраттарының қосындысын есептейміз:

6. Әрбір бақылау үшін орташа арифметикалық шама мен шаманың айырмасының көбейтіндісін есептеңіз
7. Сумманы есептеңіз
8. Алынған мәндерді
Пирсон корреляция коэффициентінің формуласына қоямыз:
9. Қорытынды: Корреляция коэффициентінің мәндер кестесіне сәйкес
әлсіз теріс корреляция деген қорытындыға келеміз.​

Талқылауға арналған сұрақтар:
1. Функционалдық және корреляциялық тәуелділіктер.
2. Параметрлік (Браве-Пирсон корреляция коэффициенттері және корреляциялық қатынас) және параметрлік емес (Спирман, Кендалл) байланысты бағалау әдістері.
3. Корреляциялық қатынастар. Жалған корреляция мәселесі. Корреляциялық плейад әдісі.
4. Сапалық белгілерді бағалау кезінде корреляция коэффициенттерін анықтау. Атау шкаласы. Ассоциация коэффициентін есептеу. Дұрыстығын тексеру.
5. Корреляциялық қатынастар. Фишер критерийі бойынша корреляция формасын анықтау. Үш немесе одан да көп белгілердің өзара байланысы.
6. Бравэ Пирсонның сызықтық корреляция коэффициенті.
7. Корреляцияның дәрежелік коэффициенті. Корреляция коэффициентінің сенімді шекаралары, корреляция коэффициентінің статистикалық маңыздылығын бағалау, екі корреляция коэффициентін салыстыру.

Корреляциялық талдау 2 негізгі міндетті шешуден тұрады:
1. Байланыс формасын анықтау, яғни функция түрін табу;
2. Байланыс күшін(тығыздығын) анықтау, яғни х әртүрлі мәндер үшін у дәрежесін бағалау.
Белгілер арасындасындағы статистикалық байланысты белгілердің тәжірбиелік мәндерінен ең төмен ауытқып, эксперименттік материалда байқалатын негізгі заңдылықты білдіретін математикалық функцияның көмегімен беруге тырысады.
Байланыс теңдеулері(немесе регрессия теңдеулері ) болатын функциялар байқалу формасы бойынша мынадай болады:
1. түзу сызықты;
2. қисық сызықты(параболалық, гиперболалық, дәрежелік және т.б.).
Байланыс формасын таңдауда, бірінші кезекте, қисықтың сол немесе басқа типі құбылыстың немесе процестің шынайы табиғатын, физикалық мәнін белгілейтіндігін ескеру қажет. Байланыс формасын графикалық анықтау үшін тәжірбиелік деректерді арнаулы корреляциялық кестеге немесе корреляциялық торға енгізеді.

Функционалдық және корреляциялық тәуелділіктер
Статистикада қоғамдық құбылыстар пен процестердің арасындағы өзара байланысты анықтамай тұрып алдымен сол өзгеріске әсерін тигізетін факторлары мен нәтижелі белгілері арасындағы тәуелділікті анықтайды. Оның өзі құбылыстың ерекшелігіне қарай функционалдық және корреляциялық байланыс болып екі түрге бөлінеді.
Функционалдық байланыс деп бір белгі мәнінің өзгеруіне әсерін тигізетін екінші бір белгінің сәйкес келуін, яғни бір факторлы белгінің өзгерісі салдарынан нәтижелі белгі мәнінің өзгеруін айтады.
y=f(xi) мұнда y-нәтижелі белгі, xi-факторлық белгі, f(xi) осы екі белгі арасындағы функционалдық байланыс.
Қоғамдық құбылыстардың өзгеруіне әртүрлі кездейсоқ факторлардың әсер етуін корреляциялық байланыс деп айтады. Статистикада корреляциялық байланыс деп нәтижелі және факторлы белгілер арасындағы сәйкестіктің болмауын айтады.
yi=f(xi)+Еі
мұнда f(xi) корреляциялық байланыста белгілі болған f пен уі арасында және ерекше алынған бір немесе бірнеше факторлық белгінің әсерінен қалыптасқан нәтижелі белгі бөлігі. Еі - жанама және кездейсоқ факторлардың әсерінен пайда болған нәтижелі белгінің бөлігі.
Түзу сызықты байланыста себепті ықпалдар белгі мәндерінің өсуіне немесе кемуіне қарай нәтижелі белгі мәндері бірқалыпты әрі үздіксіз өседі немесе кемиді.

Параметрлік (Браве-Пирсон корреляция коэффициенттері және корреляциялық қатынас) және параметрлік емес (Спирман, Кендалл) байланысты бағалау әдістері.
Статистикалық әдістердің немесе тестердің корреляция дәрежесін есептейтіни немесе жалпылауды мүмкін ететін 2 түрі бар.
Бірінші түрі ол өте кең қолданылатын параметрлік әдістер, оларға орташша мән, дисперсия сияқты параметрлер қолданылады.
Екіші түрі ол параметрлік емес әдістер, олар мына жағдайда, зерттеуші өте аз таңдау көлемімен немесе сапалы мәліметтермен жұмыс жасағанда өте құнды жәрдемін береді, бұл әдістер өте қарапайым болып келеді себебі қолдануда, есептеуде өте ыңғайлы болады.
Параметрлік емес әдістердің бір маңызды міндеттерінің бірі ол популяцияның бір бөлігінде алынған мәліметтерді анализдеу, соның арқасында жалпы барлық популяцияға қорындынды жасау мақсатын орындайды.