Корреляция структуры ксенобиотика и его токсичности. Топологические индексы

Введение
Установление соответствия между строением и биологическими свойства соединений положили начало поиску активных групп или ядер, ответственных за активность или токсичность. Объяснения корреляции структуры ксенобиотика получило свое объяснение к концу прошлого века.

Практичность
При создании нового лекарства сначала синтезируют ряд его аналогов.
В качестве кандидата выбирают вариант с наиболее оптимальными физико-химическими свойствами, характеристиками распределения, биотрансформации и минимальной токсичностью.
Для этого используют метод ККСА – метод количественных корреляций структура-активность.

Дексрипторы
Выявление количественной корреляции свойств химических соединений с их молекулярными структурами возможно после математического описания и цифрового представления структуры молекулы.
В настоящее время предложено более различных видов структурного описания(дескрипторов)

Топологические индексы
Для количественного определения наибольшую популярность имеют топологические индексы.
Первый такой индекс был предложен Х.Винером в 1947г.
Молекулярную структуры также можно показать с помощью графа. Ребра графа – ковалентные химические связи.

Топологические матрицы смежности
Исходя из графа, строят топологические матрицы смежности, расстояния и обхода.
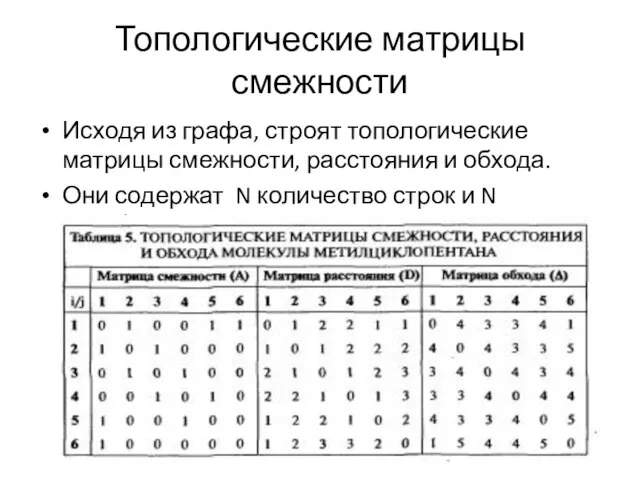
Они содержат N количество строк и N столбцов.

Матрицы
Матрица смежности - связь между вершинами.
Матрицы расстояния – равны кратчайшему расстоянию между вершинами.
Матрица обхода – самое длинное расстояние между парами атомов.

Индексы Винера, Балабана и индекс обхода