Содержание
- 2. Жоспар: I Кіріспе II Негізгі бөлім 2.1 Регрессия түсінігі 2.2 Жұпталған қарапайым регрессия 2.3 Көптік регрессия
- 3. Кіріспе Регрессиялық талдау – бір немесе бірнеше белгілердің (факторлық белгілердің) және салдардың (нәтижелі белгілердің) арасындағы байланысты
- 4. Регрессия терминін алғаш рет биометриянң негізін салушы Ф.Гальтон енгізген , оның ойын ізбасары К.Пирсон дамытқан Френсис
- 5. Регрессия түрлері Белгілердің санына қарай регрессияны екіге бөледі. Олар:
- 6. Жұпталған регрессия Жұпталған регрессия- екі факторлар арасында құрылатын модель. Мысалы, моделді құру кезінде тауардың тұтынымы кіріске
- 7. y=f(x) регрессиялық талдау келесі кезеңдерден тұрады: Функция түрін анықтау; Регрессия коэффициенттерін анықтау; Нәтижелі белгінің теориялық мәндерін
- 8. Көптік регрессия Көптік регрессия- теңдеуге басқа да факторлардың әсері болуы жағдайында құрылатын теңдеу Көптік регрессия сұраныс,
- 9. Көптік регрессияны құру үшін алдымен оның моделінің құрылымын анықтау керек. Ол 2 жағадайда болады:
- 10. Көптік регрессия әдісіне енетін факторлар мына талаптарға байланысты : Олар сандық жағынан өлшемді. Егер модельге сандық
- 11. Егер p факторы бар модель құрылса, онда ол үшін детерминация көрсеткіші R2 детерминация көрсеткіші есептелуі тиіс,
- 12. Артық факторлары бар модель қалдық дисперсияның шамасын кемітпейді және t-Стьюдент критерийі бойынша статистикалық мәнсіздікке әкеліп соғады.
- 13. Байланысты сипаттау үшін келесі жұпталған регрессия теңдеулерінің түрлерін қолданады:
- 14. Регрессия теңдпуін құру оның коэффициенттерін (параметрлерін) бағалауға әкеліп соқтырады, ол үшін ең кіші квадраттар әдісін қолданады
- 15. Ең кіші квадраттар әдісі бойынша у=a+bx мұндағы a – еркін коэффициент, b – регрессия коэффициенті, бірлік
- 16. Регрессия коэффициентінің статистикалық маңыздылығын бағалау үшін Стьюденттің t-белгісі қолданылады
- 17. Регрессия талдаудың сапалық өлшемінің негізгі өлшемінің негізгі көрсеткіші детерминация коэффициенті болып (R²) табылады
- 19. Скачать презентацию
















 Заболевания ЖКТ у студентов медицинского факультета
Заболевания ЖКТ у студентов медицинского факультета Заболевания ИППП
Заболевания ИППП Федеральный закон Об обращении лекарственных средств
Федеральный закон Об обращении лекарственных средств Әр түрлі аурулардағы диетотерапия
Әр түрлі аурулардағы диетотерапия Анатомия человека
Анатомия человека Инфузионная терапия. Забор крови для лабораторных исследований
Инфузионная терапия. Забор крови для лабораторных исследований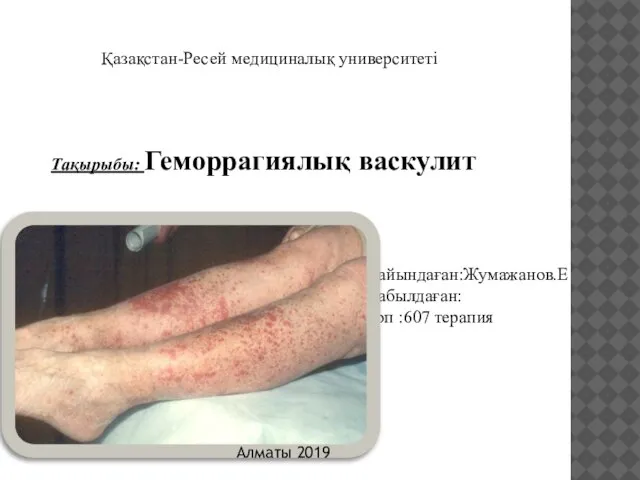 355526
355526 Органы кровообращения
Органы кровообращения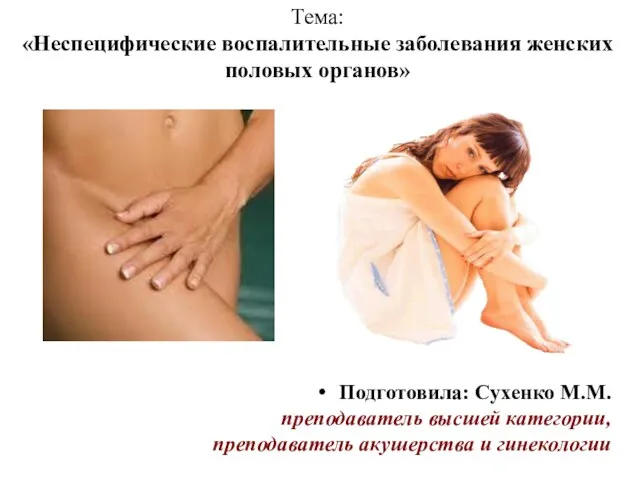 Неспецифические воспалительные заболевания женских половых органов
Неспецифические воспалительные заболевания женских половых органов 6 еңбек ресурстарын пайдалану
6 еңбек ресурстарын пайдалану Производственный травматизм на полигоне
Производственный травматизм на полигоне Первая помощь при кровотечениях
Первая помощь при кровотечениях Консервативное лечение пациентов с состоявшимся гастродуоденальным кровотечением язвенной этиологии
Консервативное лечение пациентов с состоявшимся гастродуоденальным кровотечением язвенной этиологии Гортань. Топография гортани
Гортань. Топография гортани Тромбоцитозы. Классификация
Тромбоцитозы. Классификация 3 главных буквы или ПМП в детском лагере
3 главных буквы или ПМП в детском лагере Сестринская деятельность в решении проблем детей с сахарным диабетом i типа в условиях поликлиники
Сестринская деятельность в решении проблем детей с сахарным диабетом i типа в условиях поликлиники Сердечная недостаточность
Сердечная недостаточность Массаж стоп
Массаж стоп Мочевыделительная система
Мочевыделительная система Руководство-презентация для участников олимпиады по акушерству, гинекологии и перинатологии
Руководство-презентация для участников олимпиады по акушерству, гинекологии и перинатологии Особенности эпидемического процесса при туляремии
Особенности эпидемического процесса при туляремии Острый гематогенный остеомиелит
Острый гематогенный остеомиелит Игры на приеме у психотерапевта
Игры на приеме у психотерапевта Особенности речевого развития умственно отсталых детей
Особенности речевого развития умственно отсталых детей Операции на костях
Операции на костях Респираторлы дистресс-синдромының медикаментозды терапиясы
Респираторлы дистресс-синдромының медикаментозды терапиясы Повреждения верхней конечности
Повреждения верхней конечности