Движения графиков функций

Рассмотрим некоторые виды движения графиков функций.
f(x) f(x + а)
f(x) f(x) + b
f(x) - f(x)
f(x) f( x )
f(x) f(x)
Пусть y=f(x) – исходная функция.
Задания для самостоятельной работы

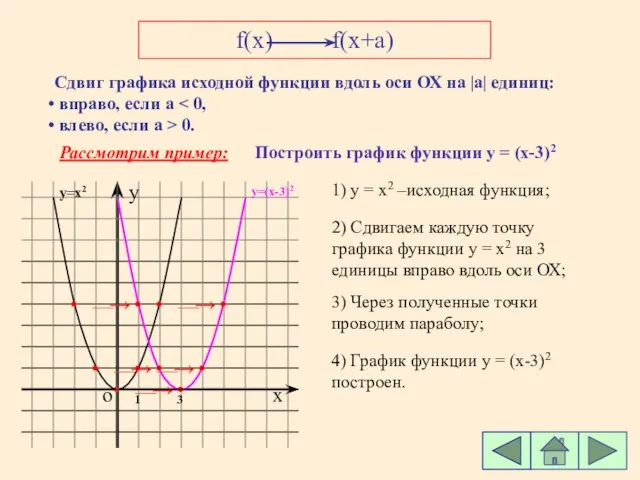
f(x) f(x+a)
Сдвиг графика исходной функции вдоль оси ОХ на |а| единиц:
вправо, если а < 0,
влево, если а > 0.
Рассмотрим пример:
о
х
y
1
y=x2
Построить график функции у = (x-3)2
1) y = x2 –исходная функция;
2) Сдвигаем каждую точку графика функции у = x2 на 3 единицы вправо вдоль оси ОХ;
3) Через полученные точки проводим параболу;
4) График функции у = (x-3)2 построен.
у=(x-3)2
3
•
•
•
•
•
• ⎯→
• ⎯→
• ⎯→
• ⎯→
• ⎯→

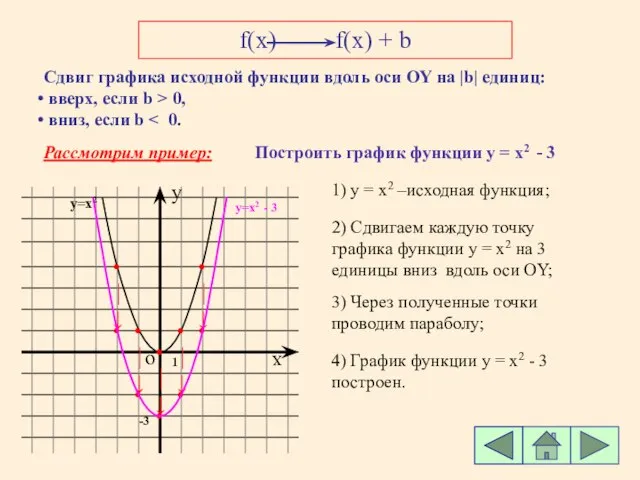
f(x) f(x) + b
Сдвиг графика исходной функции вдоль оси ОY на |b| единиц: вверх, если b > 0,
вниз, если b < 0.
Рассмотрим пример:
Построить график функции у = x2 - 3
о
х
y
y=x2
1) y = x2 –исходная функция;
2) Сдвигаем каждую точку графика функции у = x2 на 3 единицы вниз вдоль оси ОY;
•
⏐
↓
•
⏐
↓
•
⏐
↓
•
⏐
↓
•
⏐
↓
•
•
•
•
•
3) Через полученные точки проводим параболу;
у=x2 - 3
-3
1
4) График функции у = x2 - 3 построен.

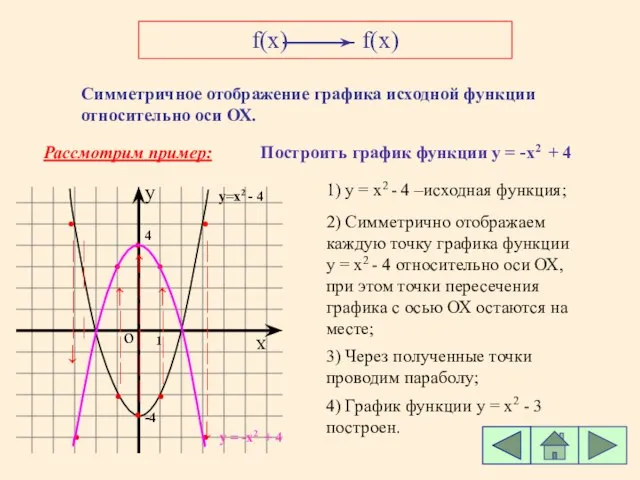
f(x) - f(x)
Симметричное отображение графика исходной функции относительно оси ОХ.
Рассмотрим пример:
Построить график функции у = -x2 + 4
о
х
y
1) y = x2 - 4 –исходная функция;
1
y=x2 - 4
2) Симметрично отображаем каждую точку графика функции у = x2 - 4 относительно оси ОХ, при этом точки пересечения графика с осью ОХ остаются на месте;
↑⏐⏐⏐⏐⏐
•
•
-4
4
↑⏐⏐
⏐
•
•
↑⏐⏐
⏐
•
•
• ⏐⏐⏐⏐
⏐
⏐⏐↓
•
• ⏐⏐⏐⏐
⏐
⏐⏐↓
•
у = -x2 + 4
3) Через полученные точки проводим параболу;
4) График функции у = x2 - 3 построен.

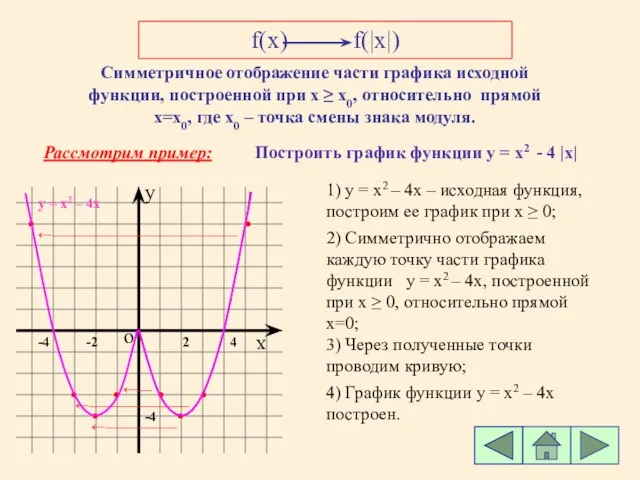
f(x) f(|x|)
Симметричное отображение части графика исходной функции, построенной при х ≥ х0, относительно прямой х=х0, где х0 – точка смены знака модуля.
Рассмотрим пример:
Построить график функции у = x2 - 4 |х|
1) y = x2 – 4х – исходная функция, построим ее график при х ≥ 0;
о
х
y
-4
2
4
2) Симметрично отображаем каждую точку части графика функции у = x2 – 4х, построенной при х ≥ 0, относительно прямой х=0;
←—————•
←——————— •
•
•
←— •
•
←————————————— •
•
3) Через полученные точки проводим кривую;
4) График функции у = x2 – 4х построен.
у = x2 – 4х
-2
-4

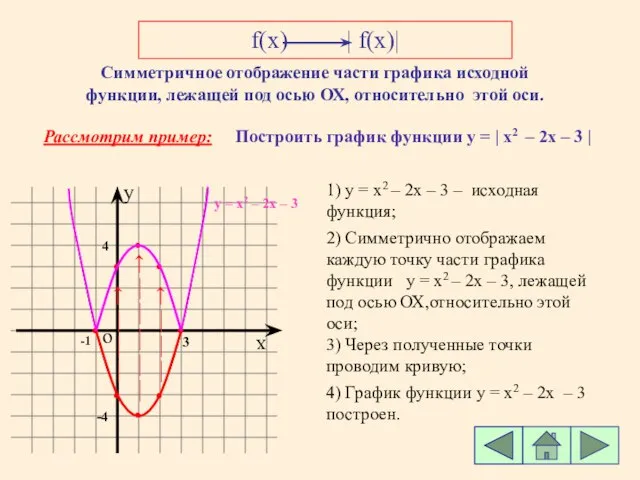
f(x) | f(x)|
Симметричное отображение части графика исходной функции, лежащей под осью ОХ, относительно этой оси.
Рассмотрим пример:
Построить график функции у = | x2 – 2х – 3 |
о
х
y
-1
3
-4
1) y = x2 – 2х – 3 – исходная функция;
2) Симметрично отображаем каждую точку части графика функции у = x2 – 2х – 3, лежащей под осью ОХ,относительно этой оси;
↑⏐⏐⏐⏐⏐
•
•
↑⏐⏐
⏐
•
•
↑⏐⏐
⏐
•
•
•
•
4
3) Через полученные точки проводим кривую;
у = x2 – 2х – 3
4) График функции у = x2 – 2х – 3 построен.

Вам предлагается выполнить построение графиков функций с использованием движения графиков
1 уровень
2 уровень
3 уровень

1 уровень
Постройте график функции с использованием движения графиков:
y =(x+2)2 ( f(x) → f(x+a) )
y = x2+1 ( f(x) → f(x) + b )
y = -x2 ( f(x) → - f(x) )
y =|x2 - 4| ( f(x) → f(x) + b, f(x) → |f(x)| )

2 уровень
Постройте график функции с использованием движения графиков:
y = - (x - 1)2 ( f(x) → f(x+a), f(x) → - f(x) )
y = |x2 - 3| - 1 ( f(x) → f(x) + b, f(x) → - f(x), f(x) → f(x) + b)
y = x2 – 4х + 5