Одночлен и многочлен

Произведение числовых и буквенных множителей и их степеней называется одночленом
Одночлены:
Алгебраические выражения:

Стандартный вид одночлена
Только один числовой множитель на первом месте – коэффициент.
Буквы записаны в алфавитном порядке
Сумму показателей степеней всех переменных называют степенью одночлена
Назовите коэффициенты одночленов:
2
-2,3
-1
1
4
7

Значение одночлена
Привести одночлен к стандартному виду
12a2b(0,5)bc =120,5a2bbc=6a2b2c
2. Заменить буквенные выражения числовыми значениями и произвести вычисления:
а=2, b=3, с=-1
6a2b2c
= 6 a2b2c
= 649(-1)=-216
2
3
-1
( )

28х2у
5х2у+23х2у=
Сложение одночленов
Одночлены, имеющие общую буквенную часть с одинаковыми показателями степеней называются подобными одночленами.
Чтобы сложить подобные одночлены, нужно сложить их коэффициенты, а буквенную часть оставить такой же.
- 8х2у
5х2у -13х2у=

5х2у23х2у=
523х2х2уу=
Умножение одночленов
Чтобы умножить одночлен на одночлен, нужно:
Перемножить коэффициенты
Сложить показатели степеней у одинаковых буквенных выражений.
115х4у2

Возведение одночлена в степень
Чтобы возвести одночлен в степень, нужно:
возвести в эту степень каждый множитель
(-0,2а3х4у)3=
(-0,2)3 (а3)3 (х4)3 (у)3=
-0,008а9х12у3

Многочлен
Алгебраическая сумма нескольких одночленов называется многочленом.
2a+b; x5+x4+x3-2; 5a2b-3ab2-3ab2+7c
По количеству одночленов в многочлене различают
двучлены:
трёхчлены:
многочлены:
3х2+100
-23р25-0,41t
-0,42х5+15у3-1
28а2-5с4+12у
x5+x4+x3-2
5a2b-3ab2-3ab2+7c

Сложение многочленов
Чтобы сложить многочлены, нужно:
Последовательно записать все члены с их знаками
Привести подобные члены
Найти сумму двух многочленов:
3ab2 + 5ab – 2a2b и
4ab2 - 8a2b + 3ab.
3ab2 + 5ab – 2a2b + 4ab2 - 8a2b + 3ab =
= 7ab2 + 8ab – 10a2b.
Стандартный вид многочлена – каждый член многочлена в стандартном виде и приведены подобные члены!

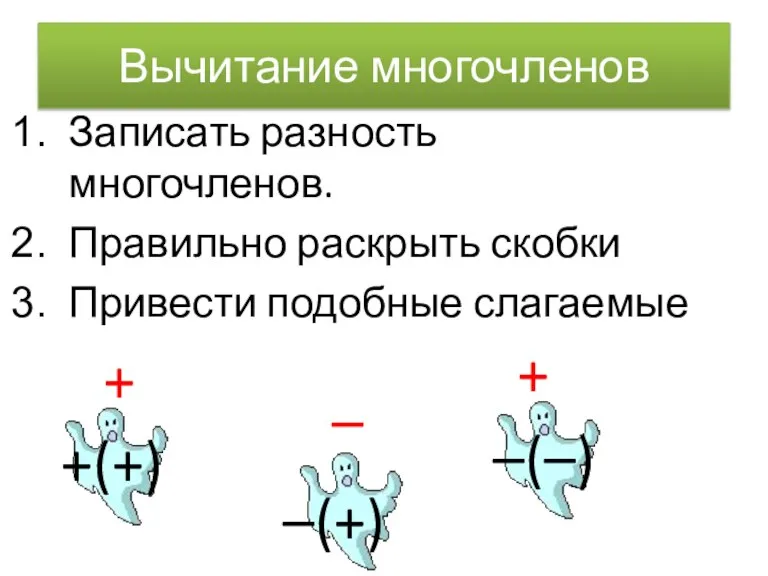
Вычитание многочленов
Записать разность многочленов.
Правильно раскрыть скобки
Привести подобные слагаемые
–(–)
–(+)
–
+
+(+)
+

–
(
–
2x
+
4
+
b
–
k
)
–(–2x+4+b–k)
+
–
–
+
=
Если перед скобками стоит знак «–»,
то при раскрытии скобок знаки
слагаемых в скобках заменяются
на противоположные.

+
+
-
Найти разность многочленов: 3m3-2m2+4m+7 и m3+m2-2m-5
3m3-2m2+4m+7 -
(m3+m2-2m-5) =
= 3m3-2m2+4m+7
-
+
-
(
-
+
m3
m2
2m
5
)
-
=
= 3m3-2m2+4m+7 –m3-m2+2m+5 =
= 2m3-3m2+6m+12.

Умножение одночлена на многочлен
Вспомним Распределительный закон умножения:
c
a
(
b
)
=
ab
+ac
a
b
+ c

К каждому дому подвели электричество

=
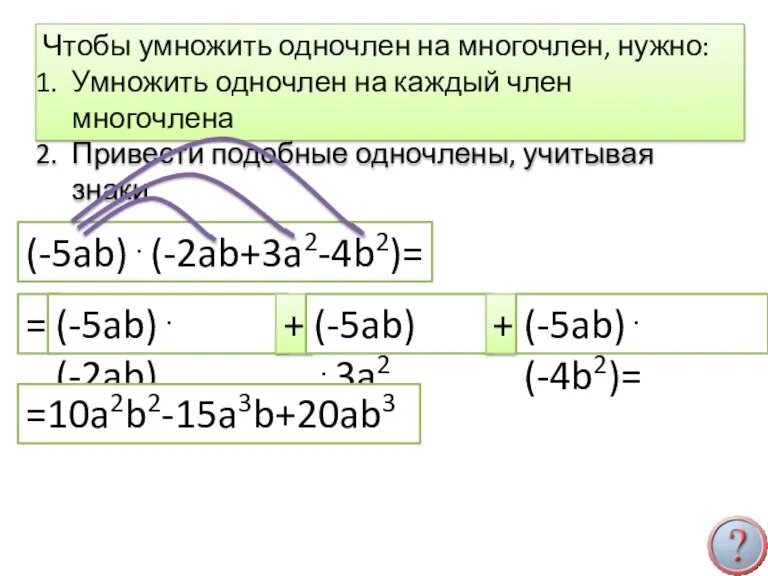
Чтобы умножить одночлен на многочлен, нужно:
Умножить одночлен на каждый член многочлена
Привести подобные одночлены, учитывая знаки
(-5ab)(-2ab+3a2-4b2)=
(-5ab)(-2ab)
+
(-5ab)3a2
+
(-5ab)(-4b2)=
=10a2b2-15a3b+20ab3

К каждому дому подвели электричество и воду

Чтобы умножить многочлен на многочлен, нужно:
Умножить каждый член первого многочлена поочередно на каждый член второго многочлена
Полученные произведения сложить.
(a+b)(c+d+e)=ac+ad+ae +bc+bd+be
(-a-b) (-5ab+a2-4b2)=
=5a2b-a3+4ab2+5ab2-a2b+4b3=
= 4a2b-a3+9ab2+4b3

Чтобы разделить многочлен на одночлен, нужно:
разделить каждый член первого многочлена поочередно на одночлен
Полученные произведения сложить.
(a+b) : c=a:c+b:c
(9x2y+12xy+15xyz):(3xy)=

Разложение многочлена на множители
Разложить многочлен на множители – представить данный многочлен в виде произведения нескольких одночленов и многочленов.
b
a
a
=
+ac
Вынесение за скобки
общего множителя
a
c
b

Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
Разложить на множители:
x4y3 - 2x3y2 + 5x2.
Наибольший общий делитель коэффициентов
–1, -2 и 5 равен 1.
Переменная x входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки x2.
Переменная y входит не во все члены многочлена; значит, ее нельзя вынести за скобки.
Вывод: за скобки можно вынести x2. Правда, в данном случае целесообразнее вынести -x2. Получим:
-x4y3-2x3y2+5x2=-x2(x2y3+2xy2-5).

1. Сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель
2. Вынести в каждой группе общий множитель в виде одночлена за скобки
3. Вынести в каждой группе общий множитель (в виде многочлена) за скобки.
Алгоритм разложения многочлена на множители способом группировки:
xy-6+3x-2y=(xy+3x)+(-6-2y)=
=x(y+3)-2(y+3)=
=(y+3)(x-2).