Содержание
- 2. ГИА – 2013 г. Модуль «Алгебра» №6 «ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией
- 3. Арифметическая прогрессия Какая последовательность называется арифметической прогрессией? Какой формулой можно записать арифметическую прогрессию? Как найти разность
- 4. Повторение Арифметическая прогрессия – последовательность, каждый член которой больше предыдущего на одно и то же число.
- 5. Модуль «Алгебра» №6 Ответ: ⎕⎕⎕⎕
- 6. Модуль «Алгебра» №6 Ответ: ⎕ ⎕ ⎕ ⎕ 51=270-3n 3n=270-51 n=255:3 n=85 n∊N 123=270-3n 3n=270-123 n=147:3
- 7. Модуль «Алгебра» №6 Ответ: 24
- 8. Модуль «Алгебра» №6 Ответ: 5
- 9. Модуль «Алгебра» Дана арифметическая прогрессия: -4; -1; 2; … . Найдите сумму первых шести её членов.
- 10. Модуль «Алгебра» №6 Ответ: 20
- 11. Геометрическая прогрессия Какая последовательность называется геометрической прогрессией? Какой формулой можно записать геометрическую прогрессию? Как найти знаменатель
- 12. Повторение Геометрическая прогрессия – последовательность, каждый член которой больше предыдущего в одно и то же число.
- 13. Модуль «Алгебра» Геометрическая прогрессия (an) задана формулой . Какоe из следующих чисел не является членом прогрессии:
- 14. Модуль «Алгебра» Геометрическая прогрессия (bn) задана условиями b₁= , bn+1=3bn. Найдите b5. №6 Ответ: 40,5 Дано:
- 15. Модуль «Алгебра» (an) - геометрическая прогрессия: b4= -1, b7=27. Найдите знаменатель этой прогрессии. №6 Ответ: -3
- 16. Модуль «Алгебра» Дана геометрическая прогрессия: , 1, 4. Найдите произведение первых пяти ее членов. №6 Ответ:
- 17. Модуль «Алгебра» (bn) – геометрическая прогрессия, знаменатель которой равен 3, b₁= . Найдите сумму первых пяти
- 19. Скачать презентацию
















 vzaimno-obratnye-funkcii.ppt
vzaimno-obratnye-funkcii.ppt Бином Ньютона
Бином Ньютона Дробно-рациональные уравнения
Дробно-рациональные уравнения Арксинус, арккосинус, арктангенс и арккотангенс
Арксинус, арккосинус, арктангенс и арккотангенс Производная
Производная Урок алгебры в 7 классе Тема: «Разность квадратов»
Урок алгебры в 7 классе Тема: «Разность квадратов»  История развития Олимпийских игр в Древней Греции
История развития Олимпийских игр в Древней Греции 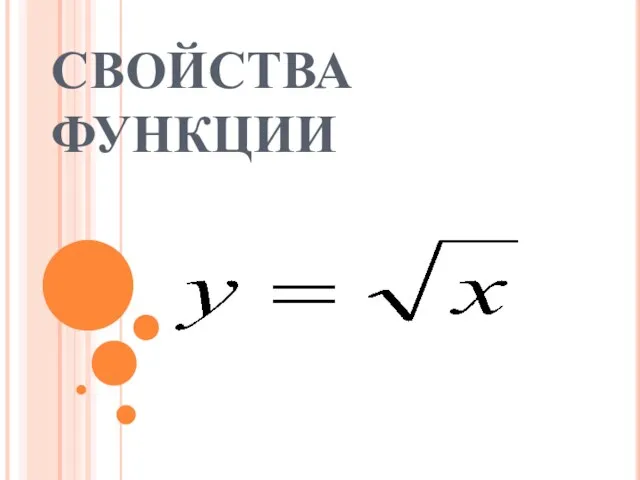 Свойства функции
Свойства функции Алгебра. Теоретический материал
Алгебра. Теоретический материал Степенная функция - презентация по Алгебре_
Степенная функция - презентация по Алгебре_ Funkcii-i-ih-svoystva-funkcionalnye-uravneniya.ppt
Funkcii-i-ih-svoystva-funkcionalnye-uravneniya.ppt Крестовые походы
Крестовые походы Презентация на тему Арбитражные аппеляционные суды
Презентация на тему Арбитражные аппеляционные суды  Презентация на тему Достопримечательности Египта
Презентация на тему Достопримечательности Египта  Обратные тригонометрические функции
Обратные тригонометрические функции Старинные ЗАНИМАТЕЛЬНЫЕ задачи
Старинные ЗАНИМАТЕЛЬНЫЕ задачи Logarifmicheskaya-funkciya.ppt
Logarifmicheskaya-funkciya.ppt Неопределённый интеграл и методы его исчисления
Неопределённый интеграл и методы его исчисления Квадратичная функция (7 класс)
Квадратичная функция (7 класс) Эпоха Просвещения в России
Эпоха Просвещения в России Размах и мода ряда чисел
Размах и мода ряда чисел Презентация на тему Основные теории местного самоуправления
Презентация на тему Основные теории местного самоуправления  Календарь история возникновения
Календарь история возникновения Свойства функций непрерывных на отрезке
Свойства функций непрерывных на отрезке Типы иррациональных уравнений Примеры решения
Типы иррациональных уравнений Примеры решения  Доказательство тождеств
Доказательство тождеств Комбинаторные задачи Перестановки РазмещенияСочетания (выборки)
Комбинаторные задачи Перестановки РазмещенияСочетания (выборки) Презентация на тему спорт как альтернативу пагубным привычкам»
Презентация на тему спорт как альтернативу пагубным привычкам»