Решение задач с помощью квадратных уравнений

Тема урока
Решение задач с помощью квадратных уравнений.

Цель урока
Продолжить формирование навыка решений квадратных уравнений по формуле.
Совершенствовать навык составления уравнения по условию задачи, умение проверять соответствие найденного решения
условиям задачи.

Уравнения вида
ax2+bx+c=0, где a≠0
называют квадратным уравнением.
Если а=1, то уравнение называют
приведенным квадратным уравнением.

В Греции математики овладели искусством решать квадратные уравнения путем использования геометрической алгебры.
Примеры геометрического решения квадратных уравнений приводятся в знаменитой «Алгебре Мухаммеда аль-Хорезми»

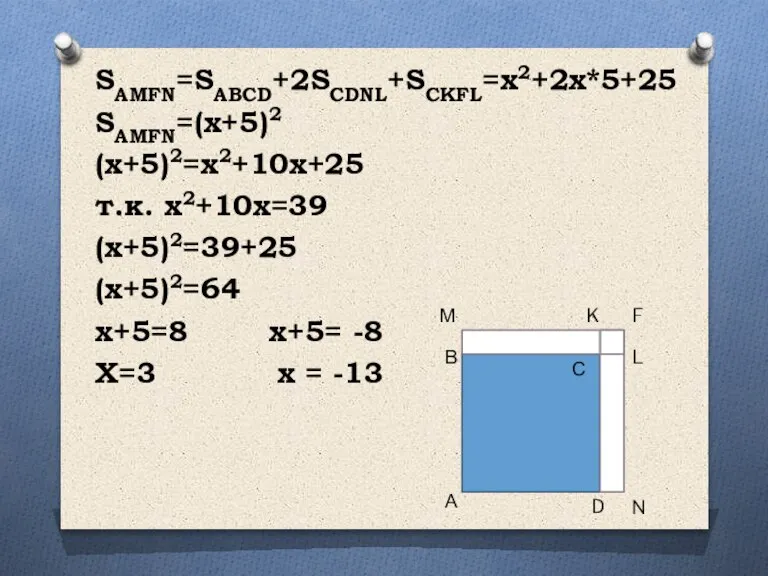
Решим уравнение x2+10x=39
Построим квадрат ABCD со стороной
х см и на его сторонах ВС и СD равные прямоугольники с высотой 5 см.
M K F
В С L
А D N

SAMFN=SABCD+2SCDNL+SCKFL=x2+2x*5+25
SAMFN=(x+5)2
(x+5)2=x2+10x+25
т.к. x2+10x=39
(x+5)2=39+25
(x+5)2=64
х+5=8 х+5= -8
Х=3 х = -13
А
В
С
D
М
F
N
K
L

Впервые отрицательные корни уравнений стал находить индийский математик Бхаскара ХII в., книга которого «Лилавати» являлась главным источником математических знаний на Востоке

В Европе решение квадратных уравнений было изложено итальянским ученым Леонардо Фибоначчи в «Книге абака» (начало ХIII в.).
В середине XVI в. в общее правило решения квадратных уравнений при любых знаках коэффициентов было дано немецким математиком М. Штифелем

Решение квадратных уравнений по формуле.

Решение квадратного уравнения
по формуле

Реши уравнения и выбери правильный ответ

Ответы

№ 1

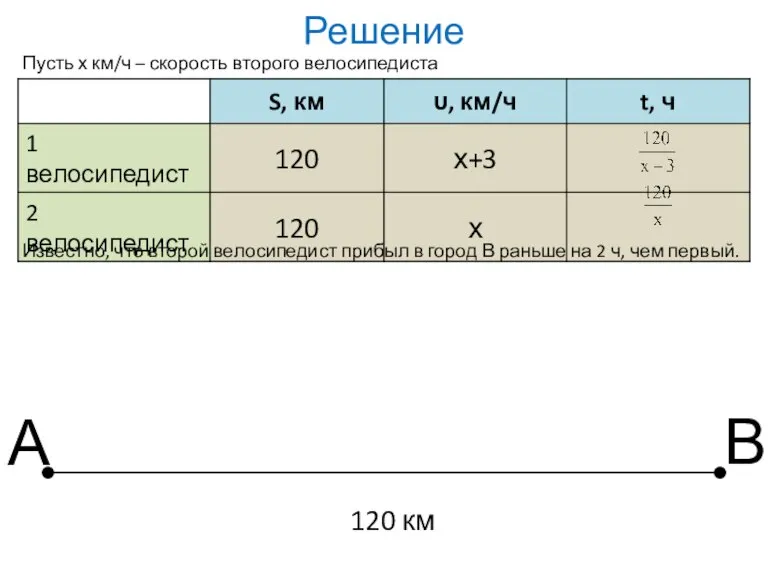
Из города А в город В, расстояние между которыми 120 км, выехали одновременно два велосипедиста. Скорость первого на 3 км/ч больше скорости второго, поэтому он прибыл в город В на 2 ч раньше. Определите скорость велосипедистов.
Условие
А
В
120 км

Решение
Пусть х км/ч – скорость второго велосипедиста
Известно, что второй велосипедист прибыл в город В раньше на 2 ч, чем первый.
А
В
120 км

Решение
Составим и решим уравнение:
Умножим обе части этого уравнения на x(x+3)
Ответ: 12 км/ч; 15 км/ч.
Число -15 противоречит смыслу задачи
Если х=12, то х(х+3)≠0, верно
12 км/ч – скорость второго велосипедиста
15 км/ч – скорость первого велосипедиста

Реши самостоятельно

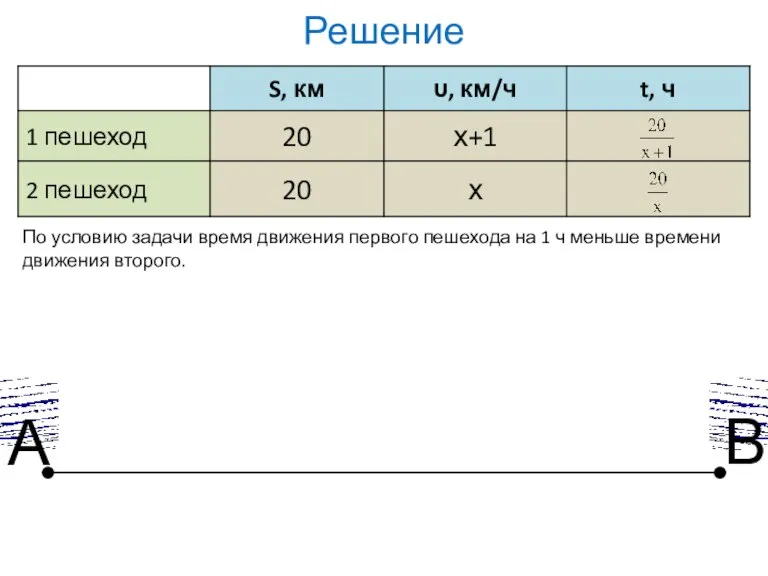
Из пунктов А и В навстречу друг другу одновременно вышли два пешехода. Скорость первого на 1 км/ч больше скорости второго, поэтому он прибыл в пункт В на 1 ч раньше, чем второй в пункт А. Найдите скорости пешеходов, если расстояние между пунктами А и В равно 20 км.
Условие
А
В

Решение
По условию задачи время движения первого пешехода на 1 ч меньше времени движения второго.
А
В

Решение
Составим и решим уравнение:
Число -5 противоречит смыслу задачи
Если х=4, то х(х+1)≠0, верно
4 км/ч – скорость второго пешехода
5 км/ч – скорость первого пешехода
Ответ: 5 км/ч; 4 км/ч.

№ 2

Катер, собственная скорость которого 8 км/ч, прошёл по реке расстояние, равное 15 км, по течению и такое же расстояние против течения. Найдите скорость течения реки, если время, затраченное на весь путь, равно 4 ч.
Условие

Решение
Известно, что время, затраченное на весь путь, равно 4 ч.
Пусть х км/ч – скорость течения реки.

Решение
Составим и решим уравнение:
Число -2 противоречит смыслу задачи
Если х=2, то (8-х)(8+х)≠0, верно
2 км/ч – скорость течения реки
Ответ: 2 км/ч.

Реши самостоятельно

Расстояние между пристанями по реке равно 21 км. Моторная лодка отправилась от одной к другой и через 4 ч вернулась назад, затратив 24 мин. на стоянку. Найти собственную скорость лодки, если скорость течения реки равна 2 км/ч.
Условие

Решение
По условию задачи время, затраченное моторной лодкой на весь путь по реке, равно
Пусть х км/ч – собственная скорость моторной лодки.