Решение простейших тригонометрических неравенств

Под простейшими тригонометрическими неравенствами понимают неравенства вида:
,где t – выражение с переменной, a∈.
Под знаком “” следует понимать любой из четырёх знаков неравенств: <, >, , .

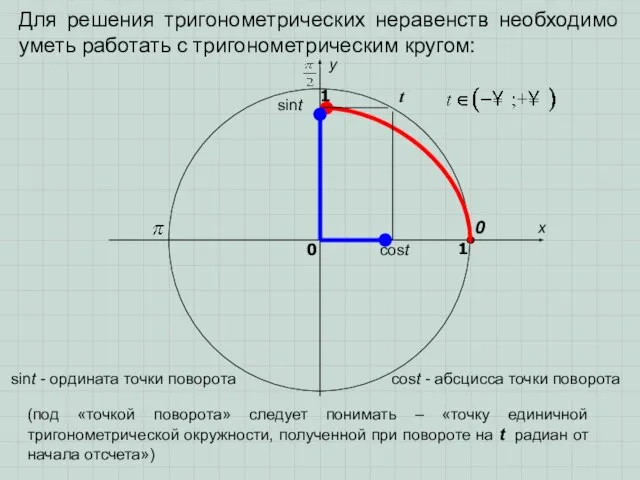
Для решения тригонометрических неравенств необходимо уметь работать с тригонометрическим кругом:
sint
cost
t
x
y
0
1
0
1
sint - ордината точки поворота
cost - абсцисса точки поворота
(под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на t радиан от начала отсчета»)

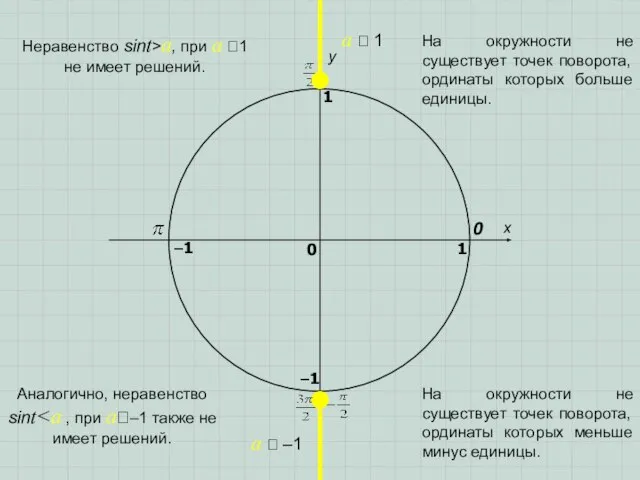
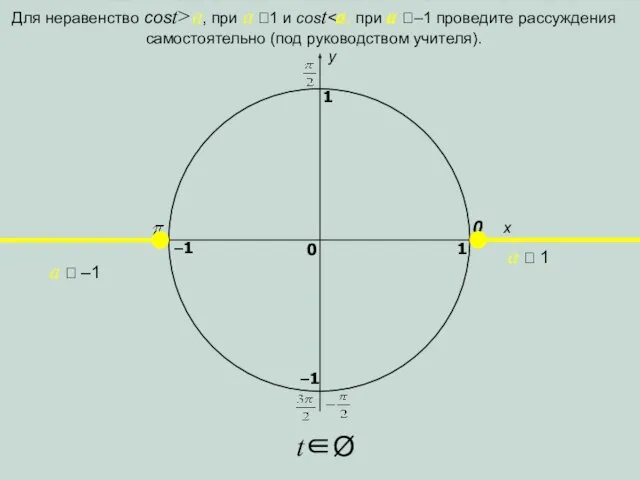
x
y
0
1
0
1
–1
–1
a  1
a  –1
Аналогично, неравенство sint имеет решений.
Неравенство sint>a, при a 1 не имеет решений.
На окружности не существует точек поворота, ординаты которых больше единицы.
На окружности не существует точек поворота, ординаты которых меньше минус единицы.

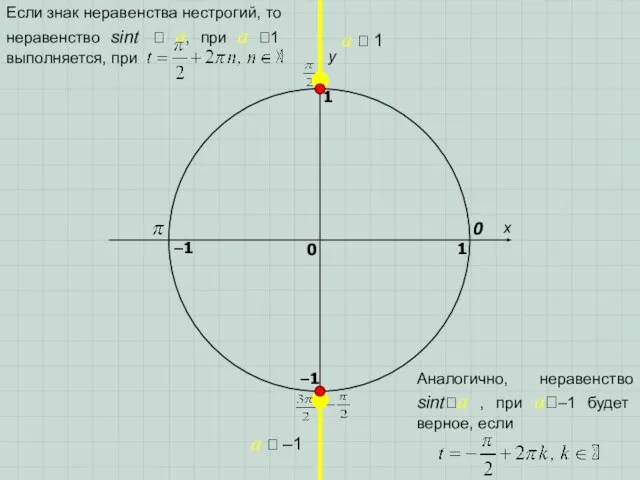
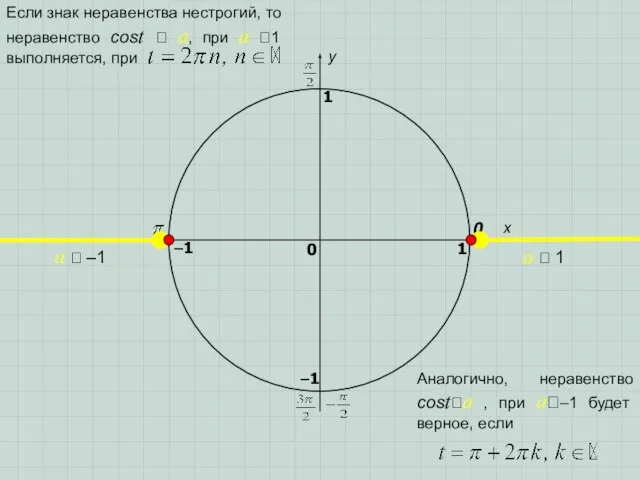
x
y
0
1
0
1
–1
–1
a  1
a  –1
Если знак неравенства нестрогий, то неравенство sint  a, при a 1 выполняется, при
Аналогично, неравенство sinta , при a–1 будет верное, если

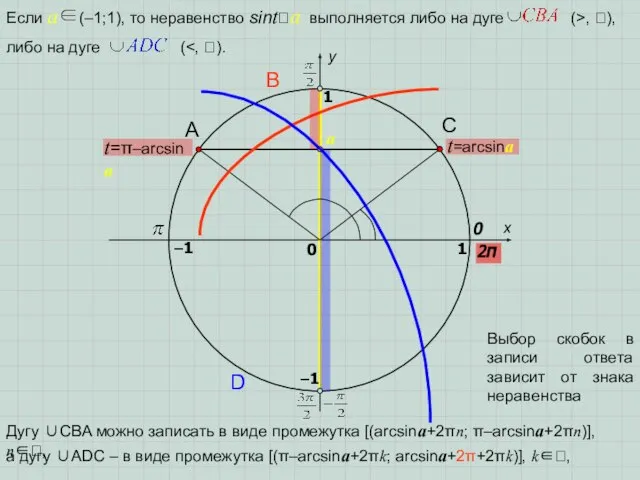
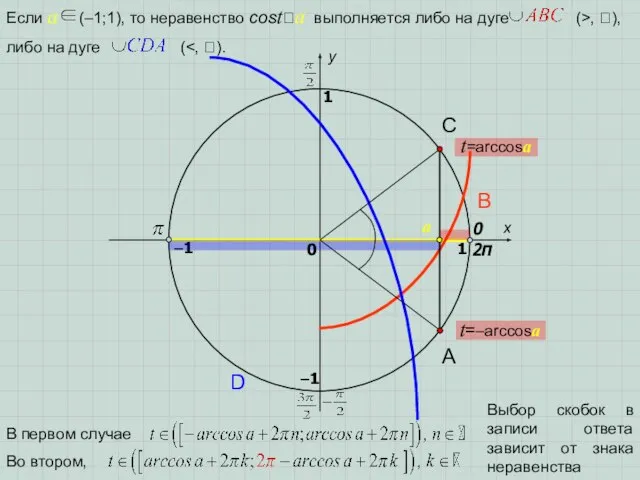
x
y
0
1
0
1
t=arcsina
t=π–arcsina
a
–1
–1
2π
A
D
B
C
Выбор скобок в записи ответа зависит от знака неравенства
Дугу ∪CBA можно записать в виде промежутка [(arcsina+2πn; π–arcsina+2πn)], n∈,
а дугу ∪ADC – в виде промежутка [(π–arcsina+2πk; arcsina+2π+2πk)], k∈,

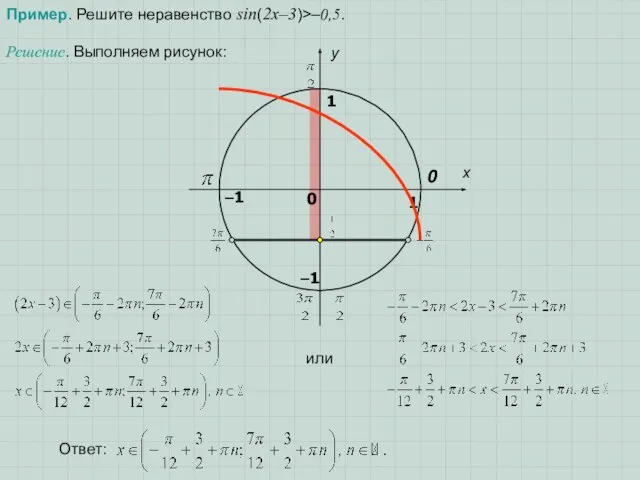
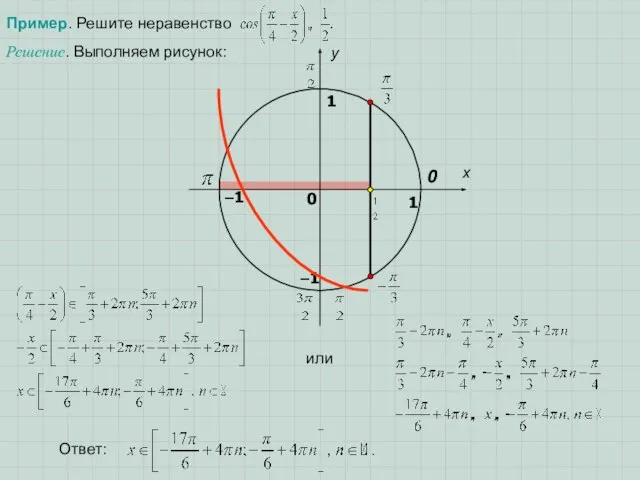
Пример. Решите неравенство sin(2x–3)>–0,5.
Решение. Выполняем рисунок:
или

x
y
0
1
0
1
–1
–1
a  –1
a  1
Для неравенство cost>a, при a 1 и cost при a –1 проведите рассуждения самостоятельно (под руководством учителя).
t∈Ø

x
y
0
1
0
1
–1
–1
a  1
a  –1
Если знак неравенства нестрогий, то неравенство cost  a, при a 1 выполняется, при
Аналогично, неравенство costa , при a–1 будет верное, если

x
y
0
1
1
–1
–1
2π
A
D
B
C
Выбор скобок в записи ответа зависит от знака неравенства
0
t=arccosa
t=–arccosa
a

Пример. Решите неравенство .
Решение. Выполняем рисунок:
или

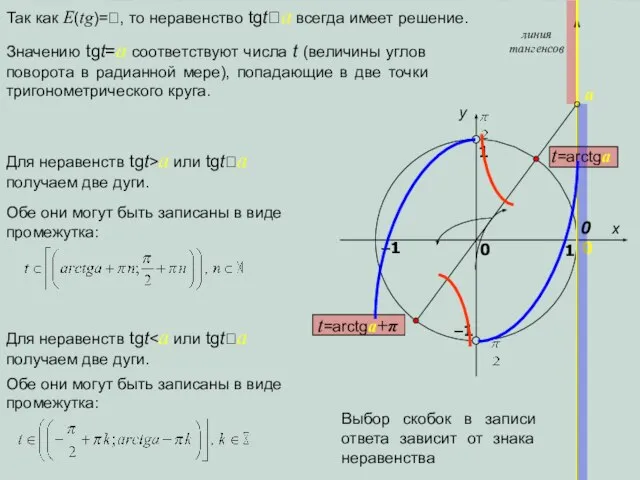
x
y
1
0
1
–1
0
линия тангенсов
a
Так как E(tg)=, то неравенство tgta всегда имеет решение.
–1
Значению tgt=a соответствуют числа t (величины углов поворота в радианной мере), попадающие в две точки тригонометрического круга.
Для неравенств tgt>a или tgta получаем две дуги.
Обе они могут быть записаны в виде промежутка:
Для неравенств tgt
0
Обе они могут быть записаны в виде промежутка:
Выбор скобок в записи ответа зависит от знака неравенства

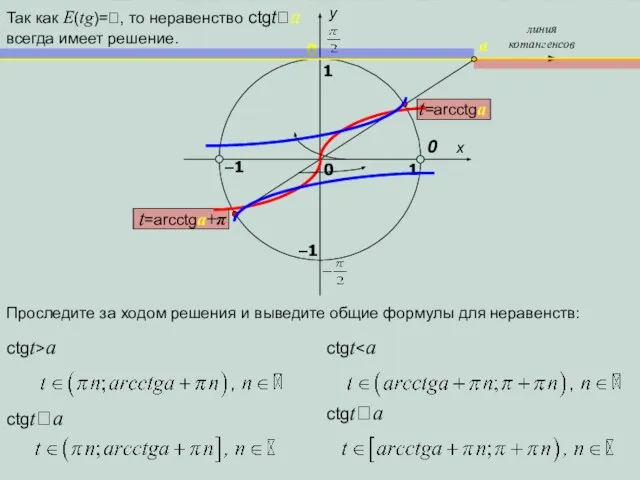
x
y
1
0
1
–1
0
линия котангенсов
a
–1
Проследите за ходом решения и выведите общие формулы для неравенств:
Так как E(tg)=, то неравенство сtgta всегда имеет решение.
0
ctgt>a
ctgta
ctgt
ctgta