Урок по теме: “Тригонометрические формулы.” Ельцова Н.Г.,учитель МОУ «Гимназия №11», Г Норильск.

Рассмотрим следующие вопросы:
радианная мера угла;
поворот точки вокруг начала координат;
определение синуса, косинуса и тангенса произвольного угла;
знаки синуса, косинуса и тангенса;
зависимость между синусом, косинусом и тангенсом одного и того же угла;
cинус, косинус и тангенс углов α и - α;

Повторим основные понятия:
координатная прямая;
координатная плоскость;
центральный угол;
sin α, cos α, где 0<α<180°;
Уравнение окружности с центром в начале координат и радиусом равным 1.

Вопрос 1: Радианная мера угла.
Каждой точке прямой ставится в соответствие некоторая точка окружности.
Кроме градусной меры угла существует еще и радианная.
Рассмотрим окр(О(0,0);R) дугу PM1, равную радиусу R.
Центральный угол,опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.

Задачи.
Найти градусную меру угла,равного
Найти радианную меру угла, равного
решение:
решение:
15º
.

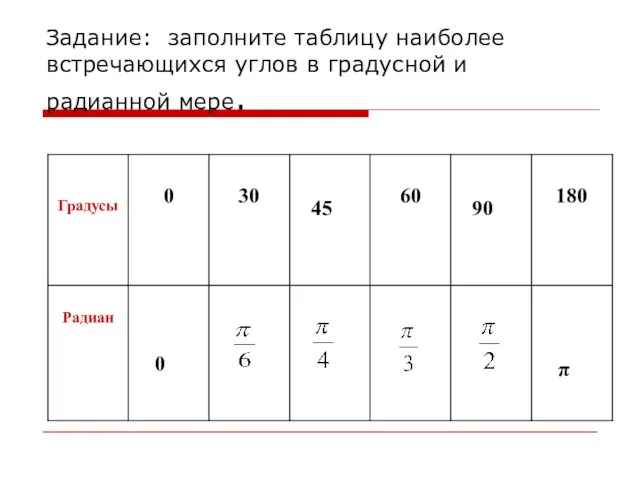
Задание: заполните таблицу наиболее встречающихся углов в градусной и радианной мере.
45
90
0
π

Вопрос 2: Поворот точки вокруг начала координат.
Установим соответствие между действительными числами и точками окружности с помощью поворота точки окружности.
Рассмотрим на координатной плоскости окружность радиуса 1 с центром в начале координат. Ее называют единичной окружностью.
Введем понятие поворота окружности вокруг начала координат на угол в a радиан, α- любое действительное число.
3. Поворот на 0 радиан, означает, что точка остается на месте.
0

Вопрос 3: определение синуса, косинуса, тангенса угла.
Синусом угла α называется ордината точки, полученной поворотом точки (1,0) вокруг начала координат на угол α.
Обозначается sin α
Косинусом угла α называется абсцисса точки, полученной
поворотом точки (1,0) вокруг начала координат на угол α.
Обозначается cos α
При повороте т.P(1,0) на угол α, т.е на угол 90 , получается точка (0,1).
Ордината точки равна 1, поэтому sin 90=sin =1.
Абсцисса точки равна 0, cos90 =cos =0

Задание:
Найти cos 270° =
sin 270° =
sin π +sin1,5π =
sin3π - cos1,5π =

Определение тангенса и котангенса угла
Тангенсом угла α называется отношение синуса угла α к его косинусу.
tg α=
Котангенсом угла α называется отношение косинуса угла α к его синусу.
ctg α=
Найдите
tg 0°=
ctg 270° =
tg 0°-tq180°=

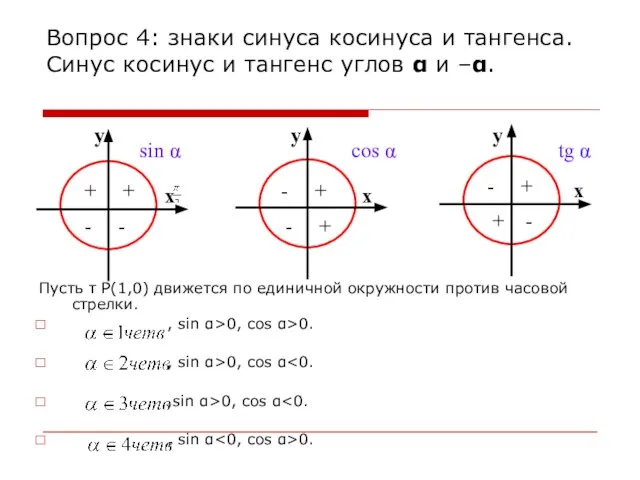
Вопрос 4: знаки синуса косинуса и тангенса. Синус косинус и тангенс углов α и –α.
Пусть т Р(1,0) движется по единичной окружности против часовой стрелки.
, sin α>0, cos α>0.
, sin α>0, cos α<0.
,sin α>0, cos α<0.
, sin α<0, cos α>0.
x
x
x
y
y
y
+ +
- +
- +
- +
+ -
- -
sin α
cos α
tg α

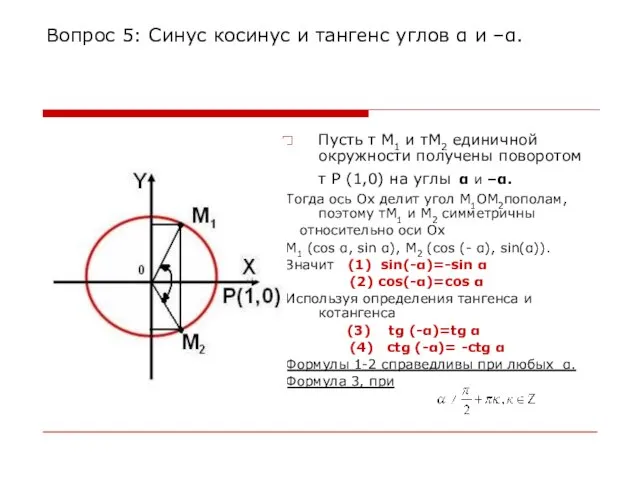
Вопрос 5: Синус косинус и тангенс углов α и –α.
Пусть т M1 и тM2 единичной окружности получены поворотом т P (1,0) на углы α и –α.
Тогда ось Ох делит угол М1OM2пополам, поэтому тM1 и M2 симметричны
относительно оси Ох
М1 (cos α, sin α), M2 (cos (- α), sin(α)).
Значит (1) sin(-α)=-sin α
(2) cos(-α)=cos α
Используя определения тангенса и котангенса
(3) tg (-α)=tg α
(4) ctg (-α)= -ctg α
Формулы 1-2 справедливы при любых α.
Формула 3, при

Задание:
1) докажите формулу (3) самостоятельно.
2) выясните знаки синуса, косинуса и тангенса углов:а) ,
б) 745°, в)-

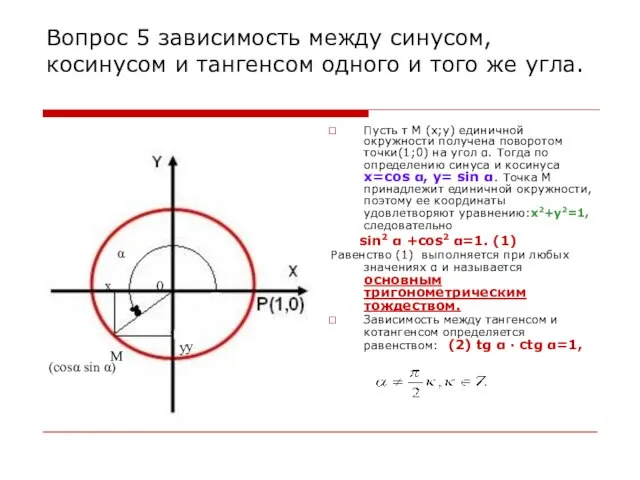
Вопрос 5 зависимость между синусом, косинусом и тангенсом одного и того же угла.
Пусть т М (x;y) единичной окружности получена поворотом точки(1;0) на угол α. Тогда по определению синуса и косинуса x=cos α, y= sin α. Точка М принадлежит единичной окружности, поэтому ее координаты удовлетворяют уравнению:х2+у2=1, следовательно
sin2 α +cos2 α=1. (1)
Равенство (1) выполняется при любых значениях α и называется основным тригонометрическим тождеством.
Зависимость между тангенсом и котангенсом определяется равенством: (2) tg α · ctg α=1,
0
α
х
у
у
(сosα sin α)
M

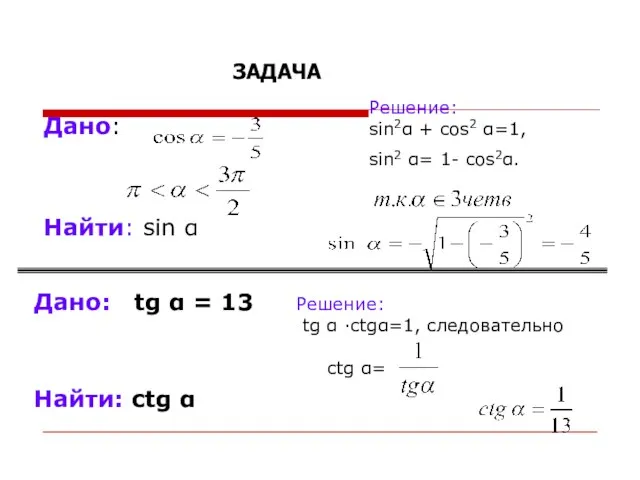
Решение:
sin2α + cos2 α=1,
sin2 α= 1- cos2α.
Дано:
Найти: sin α
Дано: tg α = 13
Найти: ctg α
Решение:
tg α ·ctgα=1, следовательно
ctg α=
ЗАДАЧА

Итог урока:
Чему равна радианная мера угла, градусная мера угла?
Какой угол называется углом в один радиан?
Что называют синусом, косинусом, тангенсом произвольного угла α?
Каким равенством определяется зависимость между синусом и косинусом одного и того же угла? Как называется это равенство?
Каким равенством определяется зависимость между тангенсом и котангенсом одного и того же угла?

1вариант 1. Найдите радианную меру угла. 2 вариант
40º 1500
ответ: ответ:
2. Найдите градусную меру угла
ответ: ответ:
3.найдите координаты точки, полученной поворотом т(1,0) единичной окружности на угол
ответ: ответ:
Математический диктант.
(0;1), (-1;0),(-1;0), (1,0)
(-1;0), (0;-1), (0;-1),(0;-1)
30° 135°