Содержание
- 2. Искусство, которое я излагаю, ново или по крайней мере было настолько испорчено временем и искажено влиянием
- 3. Задание: Решить уравнение х2 + 5х + 6 = 0. Найти сумму и произведение корней уравнения
- 4. Решение: D = 25 – 24 = 1; x1 = -2, x2 = -3. x1 +
- 5. Какое квадратное уравнение вы решили? Какую зависимость между корнями и коэффициентами вы заметили?
- 6. Дано: x2 + px + q = 0 Доказать: x1 + x2 = -p, x1 *
- 7. Таким образом, мы доказали теорему Виета для приведенных квадратных уравнений. Ее формулировка звучит так:……. Формулировка теоремы
- 8. 1. (Устно.) Чему равны сумма и произведение корней уравнения: а) х2 + 7х + 6 =
- 9. 2. Пусть х1 и х2 - корни квадратного уравнения: а) х1 = 4, х2 = -3;
- 10. О создателе теоремы Франсуа Виет родился в 1540 году в городе Фонтене ле-Конт провинции Пуату. Получив
- 11. Затем Виет приступил к разработке тригонометрии и приложению ее к решению алгебраических уравнений. В 1571 году
- 12. Но главной страстью Виета была математика. Он глубоко изучил сочинения классиков Архимеда и Диофанта, ближайших предшественников
- 13. Каждый вид уравнения с числовыми коэффициентами решался по особому правилу. Так, например, у Кардано рассматривались 66
- 14. Главное, что с этими числами можно производить алгебраические действия и в результате снова получать числа того
- 15. Такой способ записи позволил Виету сделать важные открытия при изучении общих свойств алгебраических уравнений. Не случайно
- 17. Скачать презентацию


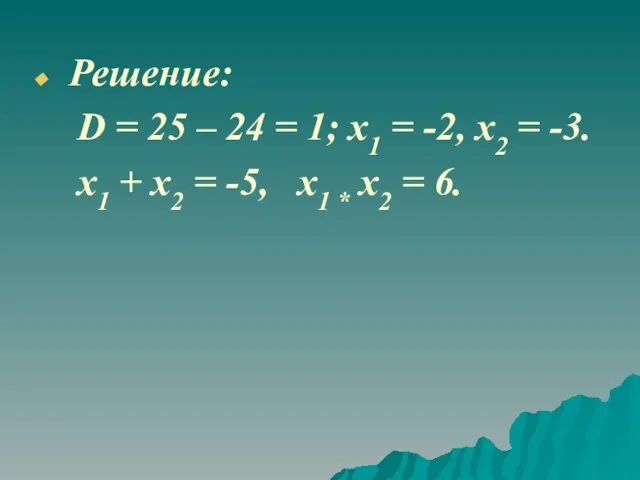











 Презентация на тему Опрос по протекционизму
Презентация на тему Опрос по протекционизму  Презентация на тему Взимание косвенных налогов в рамках Таможенного союза
Презентация на тему Взимание косвенных налогов в рамках Таможенного союза  Линейная функция
Линейная функция  Понятие логарифма Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас
Понятие логарифма Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас  Решение неравенств с одной переменной и решение систем неравенств
Решение неравенств с одной переменной и решение систем неравенств Алгебраические комедии софизмы - презентация по Алгебре
Алгебраические комедии софизмы - презентация по Алгебре ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ Урок формирования умений и навыков
ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ Урок формирования умений и навыков  Презентации по «Теореме Виета»
Презентации по «Теореме Виета» Презентация на тему Российская Федерация, субъекты Российской Федерации и муниципальные образования как субъекты предпринимател
Презентация на тему Российская Федерация, субъекты Российской Федерации и муниципальные образования как субъекты предпринимател Производная (11 класс)
Производная (11 класс) Решение задач с помощью пропорций
Решение задач с помощью пропорций Операции над событиями. Алгебраические действия с вероятностями событий
Операции над событиями. Алгебраические действия с вероятностями событий Презентация на тему Виды и особенности экологических правоотношений
Презентация на тему Виды и особенности экологических правоотношений Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей
Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей Свойства функции
Свойства функции Неравенства с двумя переменными
Неравенства с двумя переменными Понятие производной
Понятие производной Системы двух линейных уравнений с двумя переменными
Системы двух линейных уравнений с двумя переменными  Презентация на тему Основные проблемы применения коллизионного регулирования и способы их разрешения
Презентация на тему Основные проблемы применения коллизионного регулирования и способы их разрешения Производная функции
Производная функции Презентация на тему Буддизм
Презентация на тему Буддизм  Презентация на тему Система высшего образования в Японии
Презентация на тему Система высшего образования в Японии  Решение показательных неравенств
Решение показательных неравенств Экскурсия в историю математики
Экскурсия в историю математики Презентация на тему НАУКА КАК СОЦИАЛЬНЫЙ ИНСТИТУТ
Презентация на тему НАУКА КАК СОЦИАЛЬНЫЙ ИНСТИТУТ  Квадратный трехчлен и его приложения
Квадратный трехчлен и его приложения Вычисление площадей плоских фигур
Вычисление площадей плоских фигур Геометрическая прогрессия
Геометрическая прогрессия