Содержание
- 2. План урока Устная разминка Воспроизведение базовых знаний Тест «Проверь себя» Решение уравнений базового уровня Решение неравенств
- 3. Как работать Сегодня весь урок ты будешь работать самостоятельно. Ты сможешь обобщить и систематизировать знания по
- 4. 1.дату 2.тему урока: «Решение тригонометрических уравнений» Запиши в тетради:
- 5. Устная разминка Вычисли и запиши в столбик ответы в тетради: 1.arcsin 2. arccos 3. arctg 5.arcsin
- 6. Вспомни и запиши формулы для решения уравнений: 1. сos x=a, |a|≤1 х = 2. sinx=a, |a|≤1
- 7. Вспомни формулы arcsin(-a)= -arcsina для любого а [-1,1] arctg(-a)=-arctga для любого а arcсtg(-a)=π-arcсtga для любого а
- 8. Реши уравнения базового уровня Проверь ответы: х= ±π/6+2πk. х= (-1) · (-π/6) +πn/2. 3) х= +2πk,
- 9. Решение некоторых уравнений базового уровня соs(x - ) = -1/2, 3) 2соs(x - ) = -1,
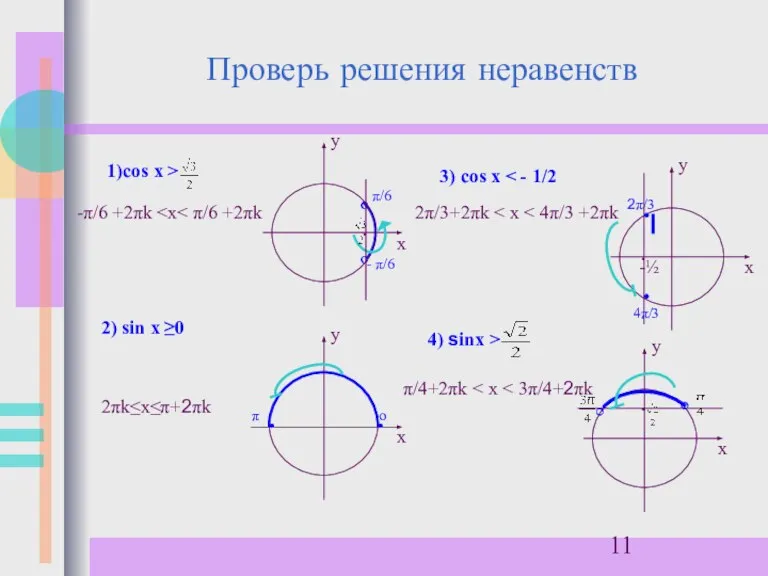
- 10. Решение неравенств Реши неравенства: 1)cos х > 2) sin х ≥0 3) cos х 4) sinх
- 11. Проверь решения неравенств 1)cos х > 2) sin х ≥0 -π/6 +2πk · - π/6 π/6
- 12. Реши уравнения повышенного уровня Проверь ответы: 1. х = +
- 13. Решение уравнений повышенного уровня х = + 3. tg(2π+х)+2tg(π/2+х)= -1, tgх- 2/tgх = -1. Умножим обе
- 14. Дополнительно 1. Реши уравнение: 2sin( -х)= и найди: а) наименьший положительный корень; б) корни, принадлежащие промежутку
- 16. Скачать презентацию





![Вспомни формулы arcsin(-a)= -arcsina для любого а [-1,1] arctg(-a)=-arctga для любого а](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/338112/slide-6.jpg)






 Презентация на тему Государственный бюджет
Презентация на тему Государственный бюджет Преобразование двойных радикалов 8 класс
Преобразование двойных радикалов 8 класс Презентация на тему Экологическое право: разминка(повторение пройденного материала)
Презентация на тему Экологическое право: разминка(повторение пройденного материала) 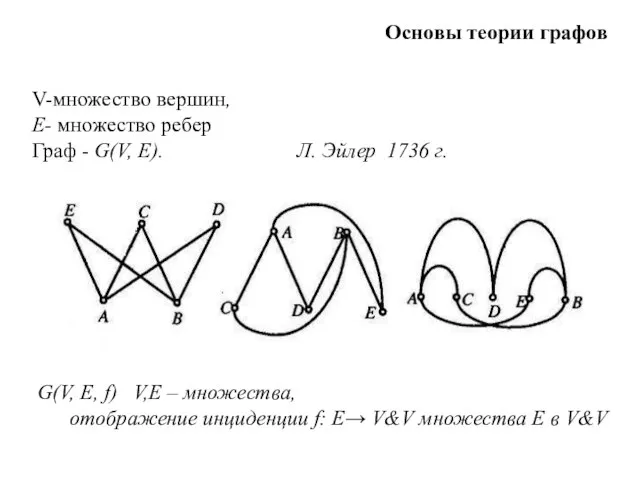 Основы теории графов
Основы теории графов Презентация на тему Театр в 18 веке в России
Презентация на тему Театр в 18 веке в России  Презентация на тему ФИЛОСОФИЯ ПРОСВЕЩЕНИЯ ВО ФРАНЦИИ
Презентация на тему ФИЛОСОФИЯ ПРОСВЕЩЕНИЯ ВО ФРАНЦИИ  Модуль
Модуль Линейная функция и ее график
Линейная функция и ее график Сложение и вычитание смешанных чисел 5 класс
Сложение и вычитание смешанных чисел 5 класс Уравнение и его корни 7 класс
Уравнение и его корни 7 класс Применение неравенств и их свойств
Применение неравенств и их свойств Презентация на тему Понятие и виды государственной службы
Презентация на тему Понятие и виды государственной службы  Квадратные уравнения 8 класс
Квадратные уравнения 8 класс Презентация на тему Виды принципов прокурорского надзора
Презентация на тему Виды принципов прокурорского надзора  Презентация на тему Внимание Внимание
Презентация на тему Внимание Внимание  «Арифметическая и геометрическая прогрессии» урок алгебры в 9 классе
«Арифметическая и геометрическая прогрессии» урок алгебры в 9 классе  Определение квадратного уравнения. Неполные квадратные уравнения
Определение квадратного уравнения. Неполные квадратные уравнения ТОЖДЕСТВА 7 класс
ТОЖДЕСТВА 7 класс  План урока
План урока Дробные рациональные уравнения
Дробные рациональные уравнения  Презентация на тему Путешествие в дальние страны АФРИКА
Презентация на тему Путешествие в дальние страны АФРИКА  Горные породы
Горные породы  Действительные числа
Действительные числа Презентация на тему Структура, полномочия и компетенция арбитражных судов федеральных округов РФ (арбитражных кассационных судов
Презентация на тему Структура, полномочия и компетенция арбитражных судов федеральных округов РФ (арбитражных кассационных судов Проценты. Задачи на концентрацию и сплавы
Проценты. Задачи на концентрацию и сплавы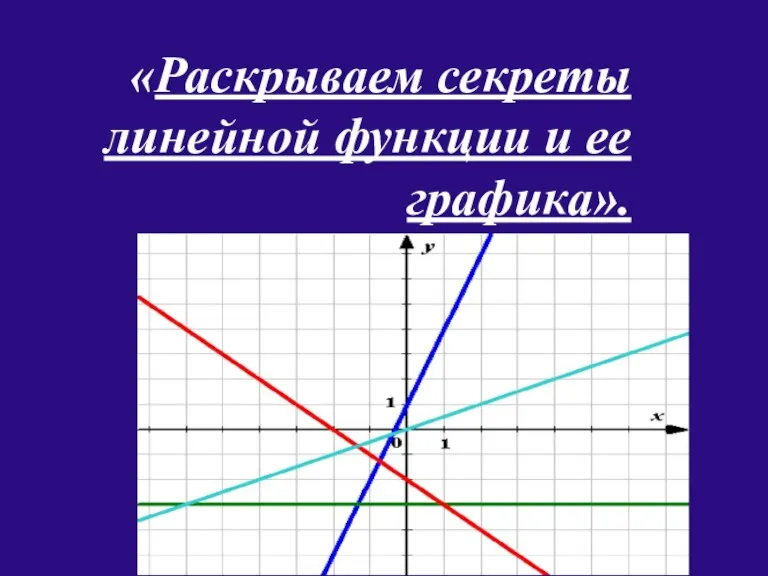 Раскрываем секреты линейной функции и ее графика
Раскрываем секреты линейной функции и ее графика Что означают слова «с точностью до …»
Что означают слова «с точностью до …» Свойства и график функции СИНУС
Свойства и график функции СИНУС