Содержание
- 2. Проблемный вопрос Можно ли находить производные, не используя определение? Существуют ли более удобные способы?
- 3. Цели и задачи Научиться находить производные элементарных функций, при этом: повторить определения приращения функции и приращения
- 4. Приращение функции и аргумента Δх = х – хо – приращение аргумента Δf(х) = f(х) –
- 5. Определение производной f ′(xо) – число Алгоритм: 1) ∆х, хо; 2) ∆f = f (хо +
- 6. у = kх + в у(хо) = kхо + в, у(хо + ∆х) = k ∙
- 7. у = х2 у(хо) = хо2, у(хо + ∆х) = (хо + ∆х)2= хо2 + 2
- 8. у = х3 у(хо) = у(хо + ∆х) = = ∆у = у(хо + ∆х) –
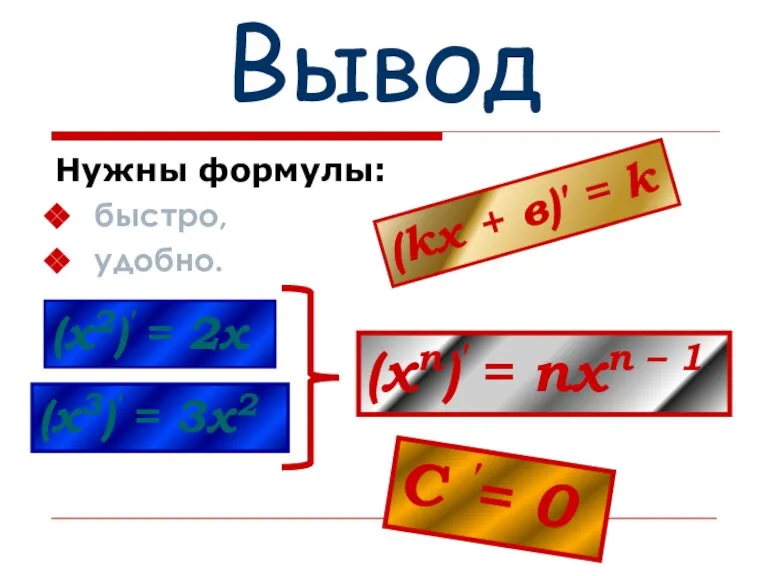
- 9. Вывод Нужны формулы: быстро, удобно. (kх + в)′ = k (х2)′ = 2х (х3)′ = 3х2
- 10. Найди производную! (х7)′ (5х3)′ (- 7х9)′ (0,5х-3)′ (9х + 16)′ (7 – 4х)′ 7. 8.
- 11. Проверь себя! 7х6 15х2 – 63х8 – 1,5х-4 9 – 4 7. 8.
- 13. Скачать презентацию




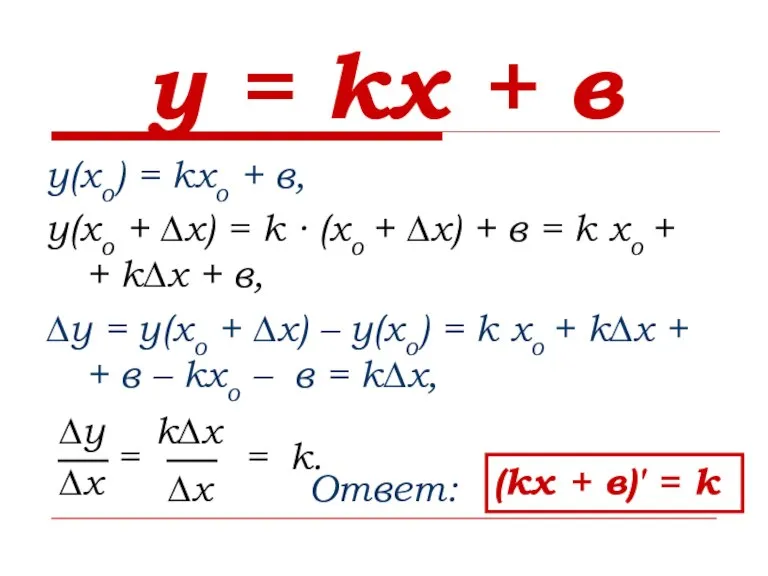

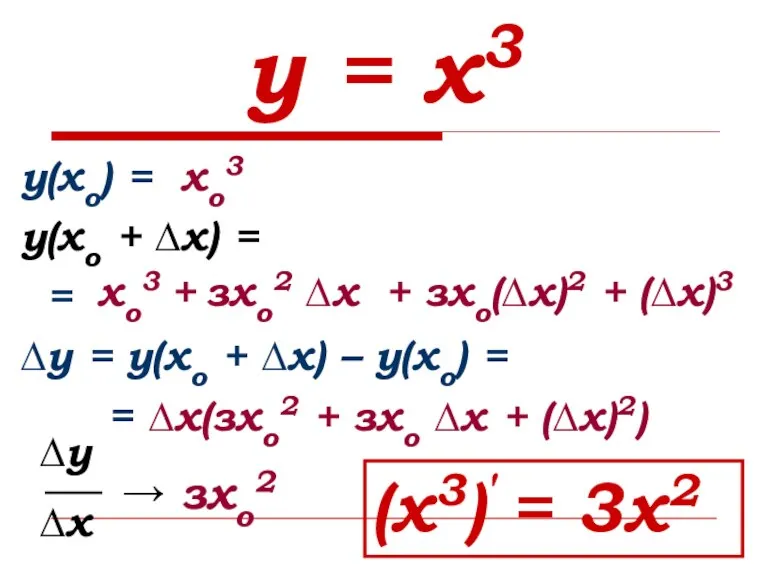


 Системы линейных уравнений с двумя переменными
Системы линейных уравнений с двумя переменными  Презентация на тему Арбитражные аппеляционные суды
Презентация на тему Арбитражные аппеляционные суды  Движения графиков функций
Движения графиков функций Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Функции 7 класс
Функции 7 класс Определение линейной функции
Определение линейной функции Презентация на тему Сертификация. Экспертиза товаров. Утилизация отходов
Презентация на тему Сертификация. Экспертиза товаров. Утилизация отходов  Понятие логарифма Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас
Понятие логарифма Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С. Лаплас  Неопределенный интеграл
Неопределенный интеграл Презентация на тему Порядок возникновения изменения и прекращения права природопользования
Презентация на тему Порядок возникновения изменения и прекращения права природопользования  Комбинаторика Размещение и сочитание
Комбинаторика Размещение и сочитание Чётные и нечётные функции
Чётные и нечётные функции Логарифмы
Логарифмы Множества и операции над ними
Множества и операции над ними Возрастание и убывание функций
Возрастание и убывание функций Презентация на тему Понятие и виды государственной службы
Презентация на тему Понятие и виды государственной службы  Презентация на тему Виды принципов прокурорского надзора
Презентация на тему Виды принципов прокурорского надзора  Функции и графики
Функции и графики Презентация на тему Графики функций синуса и косинуса и их свойства
Презентация на тему Графики функций синуса и косинуса и их свойства Линейная функция
Линейная функция  Проценты. Задачи на концентрацию и сплавы
Проценты. Задачи на концентрацию и сплавы Презентация на тему Блиц - Опрос
Презентация на тему Блиц - Опрос  Презентация на тему Путешествие в дальние страны АФРИКА
Презентация на тему Путешествие в дальние страны АФРИКА  Презентация на тему ОЩУЩЕНИЯ
Презентация на тему ОЩУЩЕНИЯ  Вычисления производных
Вычисления производных Логарифмическая функция и её приложения Шагаева А.Б. МОУ «Барагашская СОШ» 11 класс
Логарифмическая функция и её приложения Шагаева А.Б. МОУ «Барагашская СОШ» 11 класс  Презентация на тему Механистическая картина мира
Презентация на тему Механистическая картина мира