Понятие обратной функции. Определение логарифмической функции

Рассмотрим пример какой-либо функции, заданной в явном виде формулой y=f(x). Пусть, для определенности, это будет линейная функция y=2x–7. Вспомним, как выполняется такая задача: найти значение функции по заданному значению аргумента. Вспомнили?..
…Правильно: для этого надо данное значение аргумента подставить в формулу и произвести вычисления. Например, при x=2, значение функции равно y=2⋅2–7=–3.
Эту же задачу можно выполнить графическим способом. Для этого нужно:
1) построить график данной функции;
x
y
1
0
1
–7
3,5
2) отметить на оси абсцисс значение 2;
–3
2
3) получить на графике точку с отмеченной абсциссой 2;
4) найти ординату полученной в п.3 точки.
Для любой другой функции задача нахождения значения функции по заданному значению аргумента решается аналогично.

А теперь вспомним, как решается обратная задача по нахождению значения аргумента при заданном значении функции. В нашем примере с линейной функцией y=2x–7 это происходит по следующему алгоритму: в формулу, задающую данную функцию подставляют заданное значение функции и решают полученное уравнение с переменной х. Например, при у=–5 ⇒ 2x–7=–5 ⇒ х=1.
Эту же задачу можно выполнить графическим способом. Для этого нужно:
1) построить график данной функции;
2) отметить на оси ординат значение –5;
3) получить на графике точку с отмеченной ординатой –5;
4) найти абсциссу полученной в п.3 точки.
x
1
0
1
–7
3,5
–5
Для любой другой функции задача нахождения значения аргумента по заданному значению функции решается аналогично.
y
1

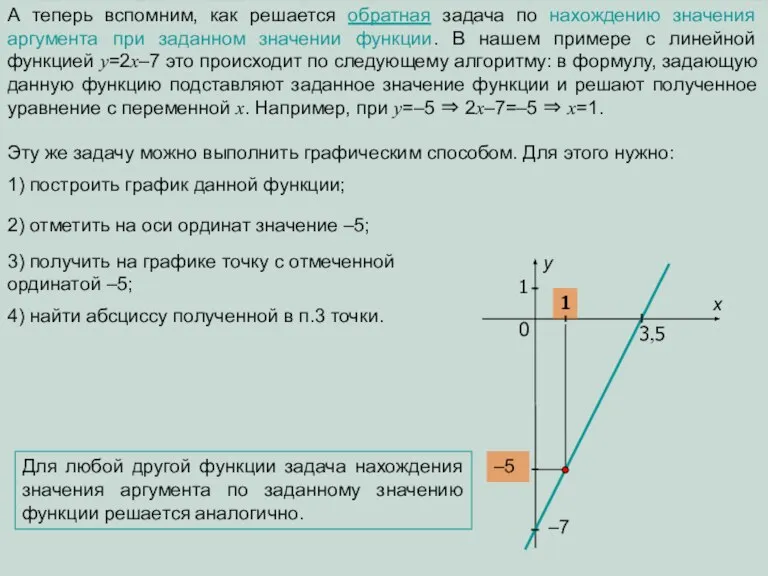
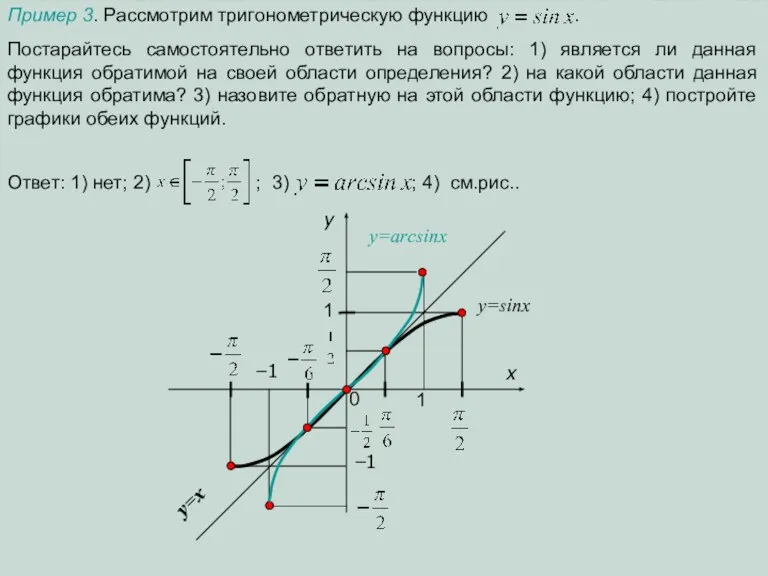
Однако, при решении обратной задачи можно поступить по-другому. Для этого составляют обратную зависимость, считая заданное значение данной функции аргументом этой зависимости. Сделать это можно двумя способами:
Выразить из формулы данной функции х через у. В нашем случае:
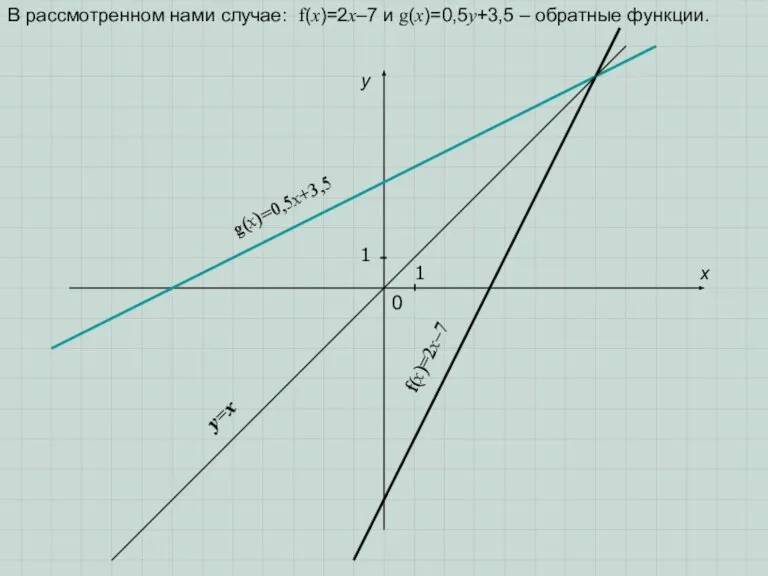
y=2x–7 ⇒ 2х=у+7 ⇒ х=0,5у+3,5. А теперь записать эту зависимость, как новую функцию, в привычном для нас виде: у=0,5х+3,5. Или
2) Поменять в формуле данной функции х и у. В нашем случае:
y=2x–7 ⇒ х=2у–7. А теперь записать эту зависимость, как новую функцию, в привычном для нас виде, выразив у через х : 2у=х+7 ⇒ у=0,5х+3,5.
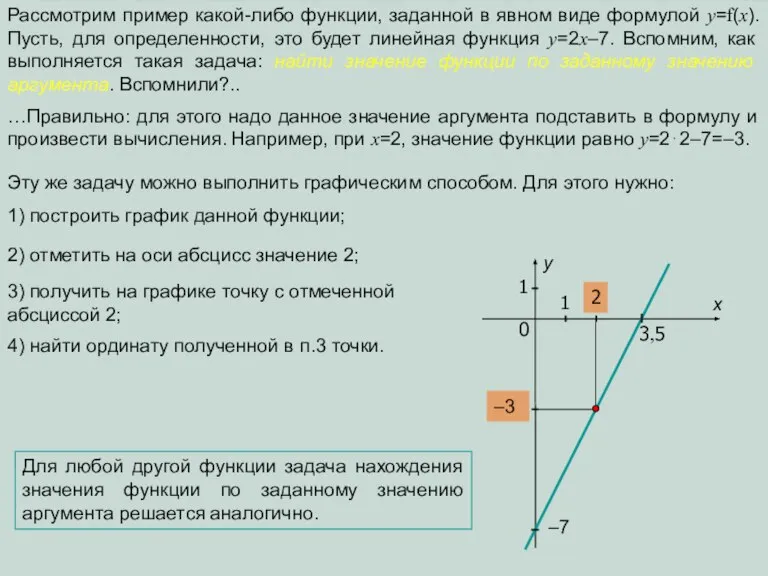
умножить на 2 и вычесть 7
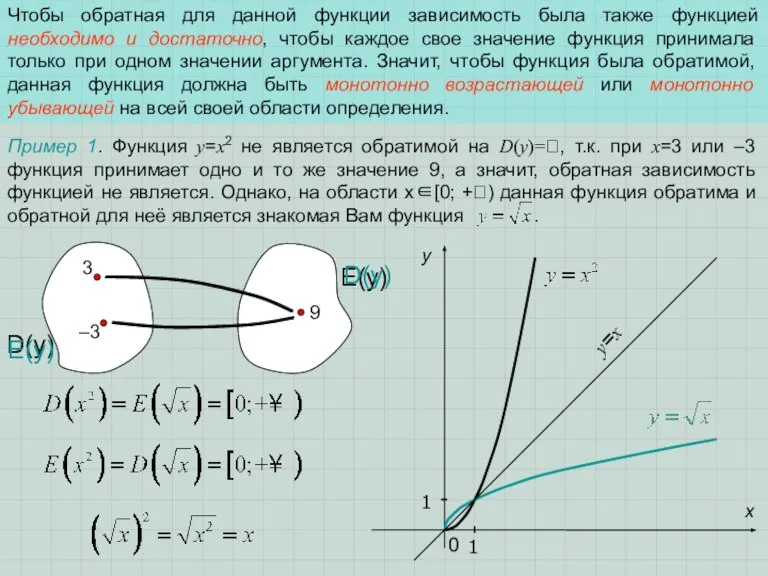
D(y) - область определения.
E(y) - область значений.
y=2x–7
прибавить 7 и разделить на 2.
D(y) - область определения
E(y) - область значений

Таким образом, мы получили обратную для функции y=2x–7 зависимость, которая является в свою очередь также функцией у=0,5х+3,5. С помощью обратной функции мы можем решать обратную задачу по нахождению значения аргумента при заданном значении данной функции. Только для обратной функции это заданное значение функции является аргументом! Значит, для
у=х=–5 ⇒ у=0,5⋅(–5)+3,5=1.
Примечание 1. Если для данной функции можно составить обратную зависимость, являющуюся также функцией, то говорят , что данная функция обратима и обратная зависимость является обратной функцией.
Примечание 2. Если функция y=f(x) является обратимой и y=g(x) – обратная для неё функция, то:
1) D(f)=E(g) и E(f)=D(g); 2) f(g(х))=g(f(х))=x.
Примечание 3. Графики данной и обратной для неё функций симметричны относительно прямой у=х.

В рассмотренном нами случае: f(x)=2x–7 и g(x)=0,5у+3,5 – обратные функции.
1
0
1
x
y
f(x)=2x–7
g(x)=0,5x+3,5
y=x

Чтобы обратная для данной функции зависимость была также функцией необходимо и достаточно, чтобы каждое свое значение функция принимала только при одном значении аргумента. Значит, чтобы функция была обратимой, данная функция должна быть монотонно возрастающей или монотонно убывающей на всей своей области определения.
1
0
1
x
y
y=x
3
–3
9
D(y)
E(y)
D(y)
E(y)

0
x
y
y=x

Постарайтесь самостоятельно ответить на вопросы: 1) является ли данная функция обратимой на своей области определения? 2) на какой области данная функция обратима? 3) назовите обратную на этой области функцию; 4) постройте графики обеих функций.
y=x

Рассмотрим теперь показательную функцию y=ax, которую Вы изучили. Так как эта функция является монотонной, в зависимости от основания степени a – монотонно возрастающей или монотонно убывающей (вспомните соответствующие условия этого), то она обратима на всей своей области определения. Составим обратную функцию описанным выше методом:
Теперь перед нами встает проблема выражения из последнего равенства переменной y (показателя степени, в который возводится положительное число a) через x, чтобы получить привычную формулу зависимости. Это делается с помощью нового понятия – логарифма числа по основанию a:
Читают так: «логарифм икс по основанию а».
Определение. Логарифмом числа x по основанию a называется показатель степени, в которую нужно возвести основание a, чтобы получить число x.
Число a называется основанием логарифма, число x называют подлогарифмическим выражением.

Примечание 3. Т.к. основание показательной функции y=ax число a>0, a1, то основание логарифма обладает такими же свойствами.
Примечание 4. Функция, заданная формулой y=logax, где a>0, a1 называется логарифмической функцией.
А теперь постарайтесь ответить на вопрос: в какую степень нужно возвести число 3, чтобы результатом этой степени получилось число 10?
3 = 10
?

y
x
1
0
1
y=ax, a>1
y=ax, 0
y
x
1
0
1
y=x
y=x
Взаимное расположение графиков показательной и логарифмической функций:
Используя данные рисунки сформулируйте и запишите свойства логарифмической функции.