Способы задания последовательностей

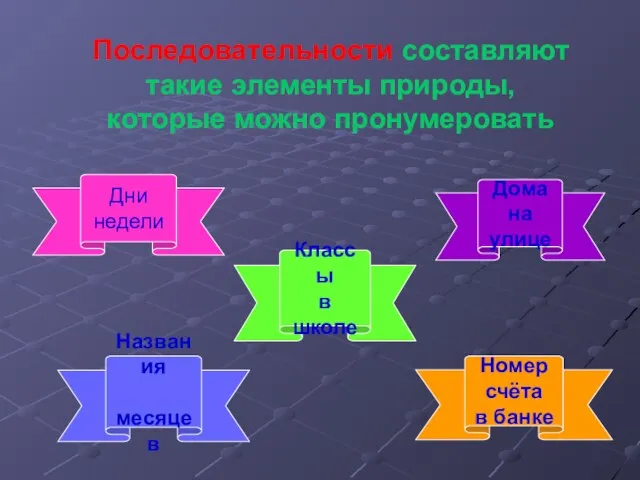
Дни
недели
Названия
месяцев
Классы
в школе
Номер
счёта
в банке
Дома
на улице
Последовательности составляют
такие элементы природы,
которые можно пронумеровать

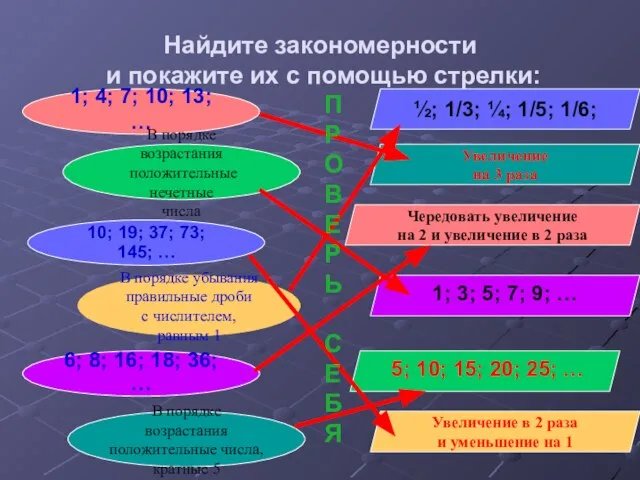
Найдите закономерности
и покажите их с помощью стрелки:
1; 4; 7; 10; 13; …
В порядке возрастания
положительные нечетные
числа
10; 19; 37; 73; 145; …
В порядке убывания
правильные дроби
с числителем, равным 1
6; 8; 16; 18; 36; …
В порядке возрастания
положительные числа,
кратные 5
½; 1/3; ¼; 1/5; 1/6;
Увеличение
на 3 раза
Чередовать увеличение
на 2 и увеличение в 2 раза
1; 3; 5; 7; 9; …
5; 10; 15; 20; 25; …
Увеличение в 2 раза
и уменьшение на 1
П
Р
О
В
Е
Р
Ь
С
Е
Б
Я

Рассмотренные числовые ряды –
примеры числовых последовательностей
Обозначают члены последовательности так
а1; а2; а3; а4; … аn

Способы задания последовательностей
1. Описанием
2. Формулой общего члена
3. Рекуррентный
4.Таблицей
*

Задание последовательности описанием
Пример:
Составить последовательность, в которой на четных местах 0, на нечетных местах – 1.
Получим последовательность:
(an) 1; 0; 1; 0; 1; 0; …
*

Задание последовательности формулой
1) an= 3*n +2,
a5 = 3*5+2 17
a10 = ? 32
a100 = ? 302
2) an= 3+n ,
a5 = ? 8
a10 = ? 13
a100 = ? 103
3) an= n2+1,
a5 = ? 26
a10 = ? 101
a100 = ? 10001
4) an= 2n-1 ,
a5 = ? 16
a7 = ? 64
a10 = ? 512
*
Замечание
Числовые последовательности
являются частным случаем
функций с натуральным
аргументом.

Рекуррентный способ задания последовательности
Название способа произошло от слова «recurro» -
возвращаться.
Рекуррентной называется формула,
выражающая любой член
последовательности, начиная с
некоторого через предыдущие.
Например: an+1= 3+n можно задать:
а1 =4, an+1 = an +1
a2= a1 +1= 4+1=5,
a3= a2 +1= 5+1=6,…
*

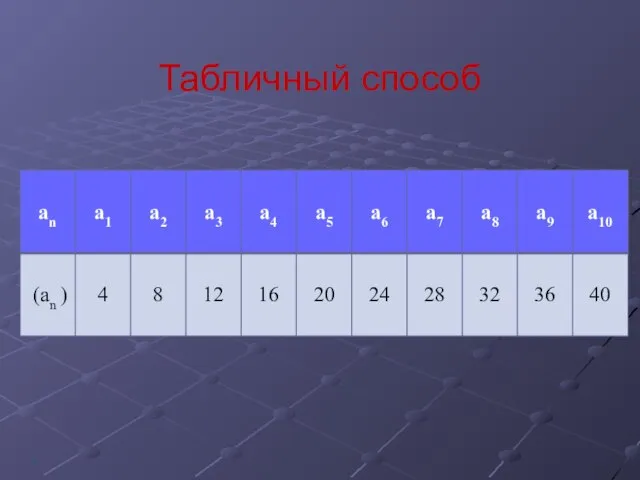
Табличный способ
*

Бесконечные последовательности:
(an) 1, 3, 5, 7, 9, 11,… - последовательность нечетных чисел (возрастающая)
(an) -5, -10, -15, -20, -25, … - последовательность отрицательных чисел, кратных 5 (убывающая)
Конечные последовательности:
(an) 1, 2, 3, 4, 5, 6, 7, 8, 9 - последовательность однозначных натуральных чисел.
(an) 10,20,30,40,50,60,70,80,90 – последовательность двузначных чисел, кратных 10.
*
Примеры
последовательностей

Последовательности заданы формулами:
an=(-1)nn2
an=n4
an=n+4
an=-n-2
an=2n-5
an=3n-1
2. Укажите, какими числами являются члены этих последовательностей
Положительные и Положительные Отрицательные отрицательные
Выполните следующие задания:
Впишите пропущенные члены последовательности:
1; ___; 81; ___; 625; … 5; ___; ___; ___; 9; … ___; ___; 3; 11; ___;
-1; 4; ___; ___; -25; … ___; -4 ; ___; ___; -7; …
2; 8; ___; ___; ___; …
16 256 6 7 8 -3 -1 27
-9 16 -3 -5 -6
26 80 242
ПРОВЕРЬ
СЕБЯ

Числа Фибоначчи
х1 =х2=1; хn+2=xn+1 +xn; n=1; 2; 3; …
Последовательность чисел Фибоначчи задается так:
Вычислим несколько
её первых членов:
1; 1; 2; 3; 5; 8; 13; 21;
34;55; 89; 144;
233; 377; …
Треугольник Паскаля
Бесконечная числовая таблица треугольной формы,
где по боковым сторонам стоят 1,
а каждое из остальных чисел равно сумме двух чисел, стоящих над ним слева и справа.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Продолжи строчку!
1 6 15 20 15 6 1

1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
Связь между числами Фибоначчи
и треугольником Паскаля
Между числами Фибоначчи
и треугольником Паскаля существует связь. Подсчитаем для каждой восходящей диагонали треугольника Паскаля сумму всех стоящих на этой диагонали чисел, получим:
Для 1 диагонали – 1;
Для 2 диагонали – 1;
Для 3 диагонали – 1+1=2;
Для 4 диагонали – 1+2=3;
Для 5 диагонали – 1+3+1=5;
Для 6 диагонали – 1+4+3=8 ...
В результате мы получаем числа Фибоначчи: 1; 1; 2; 3; 5; 8; …
Всегда сумма чисел n-ой диагонали есть n-ое число Фибоначчи.